2 - Resolvendo equações do 1^o Grau

Uma equação do 1^o grau é uma equação da forma ax+b=c, onde a, b e c são números reais quaisquer.

Exemplos:

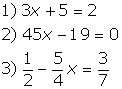Quando dizemos “Resolva a equação do 1o grau” queremos encontrar o valor para x que satisfaça a equação. Este processo será muito útil quando nos depararmos com problemas que envolvam receita, custo, lucro, oferta e demanda do primeiro grau, que será visto posteriormente.
Para obter a solução ou raiz de uma equação do 1º grau, podemos aplicar o processo dedutivo, que consistem em isolar a variável x, realizando para isto operações inversas na ordem inversa, que são retratadas pelo princípio da equivalência das igualdades que segue.

Princípio de Equivalência das Igualdades

- Princípio Aditivo

- Princípio Multiplicativo

De uma forma geral, para deslocarmos um termo de um membro para outro, se ele está somando, passamos subtraindo (ou vice-versa) e, se ele está multiplicando, passamos dividindo (ou vice-versa).

Exemplo:

Determine o valor de x que satisfaz a equação:

3x+2=8

Resolução:
Pela princípio aditivo, (item a) podemos somar -2 nos dois lados da equação que a igualdade se preserva. Obtemos:

Multiplicando ambos os membros por  a igualdade se preserva, segundo o princípio multiplicativo. Obtemos:

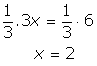
Legal, não?!
Substituindo 2 no lugar de x na equação inicial constata-se que a igualdade é verificada.