Unidade 02 - Funções 1

Nestes momentos precisamos de um pouco de paciência para tentar interpretar o que foi pedido e associar com o que temos em mão para solucionar o problema. Se fosse pedido quantos rádios o operário teria produzido as 12 horas bastava substituir o x por 4 na equação e pronto, pois a expressão só nos fornece a quantidade de rádios ao final de tantas horas. A expressão não nos fornece a quantidade de rádios entre tantas horas. Seria um engano se alguém substituísse x por 1, pois assim obteria apenas quantos rádios o trabalhador teria montado as 9 horas da manhã e não quantos foram produzidos entre 11 e 12 horas.
E daí? Como que resolvemos o item b) ? É simples, calculamos quanto o operário produziu as 12 horas depois calculamos quanto ele produziu as 11 horas e subtraímos um pelo outro. Vejamos.

<< Fechar

Exemplo 01:

Na produção de um determinado produto, uma empresa tem um custo fixo de R$400,00 mais um custo variável de R$10,00 por cada produto. Apenas com as informações dadas obtenha a função que represente o custo total da empresa.

Resolução:

Ora, o custo da empresa depende da quantidade de produtos que ela produz. Seja x a quantidade de produtos que a empresa produz e seja C o custo total da empresa na produção dos produtos. Daí,

C(x)=400+10x

Observação:

Utilizamos letras que tenham a ver com o contexto. Trataremos custo por C, lucro por L, receita por R e assim por diante.
Lembrando que o importante não é a letra que utilizamos e sim o que ela representa. Se a letra escolhida facilitar a nossa compreensão do assunto, melhor.

Exemplo 02:

Se voltarmos ao problema anterior e perguntarmos: qual o custo da empresa se 50 produtos forem produzidos? Como resolver este problema?

Resolução:

Alguns alunos poderão mentalmente encontrar a resposta para a pergunta, procedendo de forma parecida com a seguinte:

Cada produto custa R$10, eu adquiri 50, então o custo será de 50.10=500 mais ainda tem o custo fixo de R$400,00 o que perfaz R$900,00.

Usando a expressão da resolução do exemplo anterior, podemos proceder de outra forma:
Como x representa a quantidade de produtos produzidos então substituiremos x por 50 na expressão do custo, vejamos

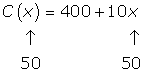
Logo,

C(50)=400+10(50)=900

A leitura da expressão acima é: 'O custo para adquirir 50 produtos é de R$900,00'.

Vejamos um exemplo mais complicado, só que agora começaremos a omitir passagens.

Exemplo 03:

Um operário que chega ao trabalho às 8 horas da manhã, terá produzido p(x)=-x³+6x²+15x rádios transistores x horas mais tarde.

a) Quantas rádios terá produzido às 10 horas da manhã?
b) Quantos rádios terá produzido entre 11 e 12 horas?

Neste problema muitos devem ter pensado:'Ora, basta substituir o x por 10 na equação. E pensaram errado!
Para quem teve este pensamento, e para quem sequer entendeu o problema, recomendamos mais uma lida no enunciado do exemplo.
Observe que a variável x no problema representa horas após as 8. Logo, devemos substituir x por 2 na equação e não por 10.

Resolução:

a) Substituindo x por 2 na equação obtemos

p(2)=-(2)³+6(2)²+15(2)=46

Logo às 10 horas (2 horas após as oito) o trabalhador terá montado 46 rádios transistores.

Como proceder no item b)?

Resolução:

b) Calculando a produção do trabalhador às 12 horas, ou seja, substituindo x por 4 na equação obtemos -(4)³+6(4)²+15(4)=92. Calculando a produção do trabalhador às 11 horas, ou seja, substituindo x por 3 na equação obtemos -(3)³+6(3)²+15(3)=72. Logo o número de rádios transistores produzidos entre 11 e 12 horas será de 92-72=20.

Recomendamos agora que realize os exercícios de fixação deste módulo. A definição de função é muito simples mas muitos se confundem com o seu significado. E matemática não se aprende apenas vendo algo pronto... É preciso um pouco de prática e os exercícios estão aí para isto.