1 - Função Demanda

A demanda de um determinado bem é a quantidade desse bem que os consumidores pretendem adquirir ao longo de um determinado tempo. Esta quantidade demandada de um produto no mercado é função de várias variáveis, por exemplo: preço por unidade do produto, preços de bens substitutos, renda do consumidor, gostos, etc. Vamos supor que todas as variáveis citadas permaneçam constantes, exceto o preço unitário do produto (p). Dessa forma, verifica-se que o preço (p) relaciona-se com a quantidade demandada (x). Assim, definimos a relação p= f(x) como função demanda e, em se tratando de ser uma função linear, podemos escrever na forma p = mx + b.

Exemplo 01 :
O número de sorvetes (x) vendidos por semana numa sorveteria relaciona-se com o preço (p) de acordo com a função de demanda:

p=10-0,002x

a) Determine a quantidade demanda por semana quando p=R$ 4,00.
b) Esboce o gráfico da função demanda.

Resolução:
a) Substituindo p=4,00 na relação funcional acima determinaremos a quantidade demandada de sorvetes:

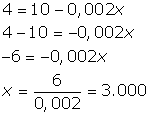
Assim se o preço for igual a R$ 4,00 teremos 3.000 unidades de sorvetes demandados por semana.

b) Como a função p=10-0,002x é linear sabemos que seu gráfico é uma reta. Logo basta encontrarmos dois pares (x, y), satisfazendo a equação, para podermos esboçar o gráfico da função demanda.

Considere arbitrariamente x = 0 e x = 3000, assim teremos:

x=0 Þ p=10-0=10
x=3000 Þ p=10-0,002.3000 Þ p=R$ 4,00