3 - Depreciação Linear
Devido ao desgaste, obsolescência e outros fatores, o valor de um bem diminui com o tempo. Essa perda de valor ao longo do tempo chama-se depreciação. Assim, o gráfico do valor de um determinado bem em função do tempo é uma curva decrescente. Nesta unidade vamos admitir que a curva de valor seja uma reta e, portanto, que a depreciação é linear. Isto significa que a perda é constante ao longo do tempo (dias, meses, anos, outros).
Dessa forma, podemos escrever uma função que descreve o valor de um bem em função do tempo, através da relação: V = mx + b.
Um raciocínio que vai ajudar na resolução dos exercícios é.... Por dedução lógica podemos afirmar que o valor de um bem daqui a x anos, será o valor dele hoje menos a perda total ocorrido neste período de x anos. Correto?
De forma matemática,
V(x) = VH - dx
Exemplo 04 :
| O valor de uma máquina hoje é R$1000,00 e estima-se que dentro de 6 anos seja R$100,00. |
| a)
Qual o valor da máquina daqui a x anos? b) Qual sua depreciação total daqui a x anos? |
Resolução:
a) Vamos inicialmente esboçar o gráfico da função que descreverá a depreciação da máquina com o passar do tempo. Estamos considerando que a depreciação é linear, logo o gráfico é uma reta. Seja x tempo e V o valor da máquina.
|
|
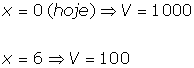 |
| Daí temos dois pontos P1=(0,1000) e P2= (6,100) | |
| Temos então o seguinte gráfico: | |
O coeficiente
angular da reta = ![]()
Assim a
equação da reta será:
V=-150x+b
Determinando n (raciocínio análogo ao exemplo sobre
função oferta).
1000=-150.0+b
1000=b
Assim
V=-150x+1000
b) A depreciação total até esta data será:
Observe que em 6 anos a perda foi de R$ 900, logo como a perda é constante ao longo dos anos, podemos concluir que a perda foi de R$ 150,00 por ano. Assim,
Perda em 1 ano =
150 = R$ 150,00
Perda em 2 anos = 2.150 = R$ 300,00
Perda em 3 anos = 3.150 = R$ 450,00
Perda em x anos = x.150 = 150x
Assim, a depreciação em x anos foi de 150x.
Exemplo 05 :
Daqui a
2 anos o valor de um computador será de R$5.000,00 e daqui a
4 anos R$4.000,00. Admitindo depreciação linear:
a) Qual é o seu valor hoje?
b) Qual seu valor daqui a 5 anos?
Resolução:
Observe
que x=2 Þ
V=5000
x=4 Þ V=4000
Daí, m= ![]()
Portanto,
V=-500x+n , substituindo x por 2 e V
por 5000, teremos:
5000=-500(2)+n Þ n=6000.
Logo, V=-500x+6000.
Para o item
a) fazendo
x=0, obteremos o valor do computador hoje, daí:
V=-500.0+6000 = 6000, ou seja, o valor do computador hoje é
$6000,00.
Vamos resolver este item de uma outra forma.....
Por dedução lógica podemos afirmar que o valor de um equipamento daqui a 2 anos, será o valor dele hoje menos a perda total ocorrido no período de 2 anos. Correto?
Em uma equação temos que: V(2) = VH – d2
Logo, V(2)
= 5000 ![]() Valor
do equipamento daqui a 2 anos
Valor
do equipamento daqui a 2 anos
VH = ? ![]() valor
do equipamento hoje (incógnita)
valor
do equipamento hoje (incógnita)
d2 = 1000 ![]() Perda total em 2 anos
Perda total em 2 anos
Assim, 5000 = VH – 1000 ![]() VH = R$ 6000,00.
VH = R$ 6000,00.
Ficou mais fácil? Escolha a forma que mais gostou...
b) Para
determinar o valor do equipamento daqui a 5 anos, basta substituir x
por 5 na função obtida e teremos:
V=-500.5+6000=3500,
ou seja, o valor do computador daqui a 5 anos será de $3.500,00.
Utilizando o raciocínio lógico explicado anteriormente, podemos escrever que:
V(5) = VH – d5.
Neste caso,
V(5) =
? ![]() Valor
do equipamento daqui a 5 anos (incógnita)
Valor
do equipamento daqui a 5 anos (incógnita)
VH = 6000 ![]() Valor do equipamento hoje.
Valor do equipamento hoje.
d5 = 2500 ![]() Perda total em 5 anos ( 5x500)
Perda total em 5 anos ( 5x500)
Finalmente, V(5) = 6000 – 2500 = R$ 3500,00.