As raízes:

Ponto de vértice: (5 , 25)
Concavidade: voltada para baixo

Com os dados acima podemos esboçar o gráfico da parábola de R(x) marcando os pontos acima no eixo cartesiano:

Vemos graficamente, e podemos provar, que o maior valor assumido pela função receita é o ponto de vértice.
Assim, o valor de x que maximiza a receita é x=5, isto é, a quantidade de unidades que ele terá que vender para obter receita máxima é x = 5.

Se fosse pedido o valor da receita máxima, este valor seria o yv, que representa o valor da receita quando x = 5. Logo, Rmáx = R$ 25,00.

b) O lucro é igual a diferença entre a receita e o custo. Logo podemos estabelecer a seguinte relação:

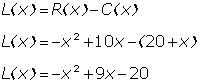
Vemos na relação acima que o lucro é uma função quadrática. Nosso objetivo é determinar o ponto de máximo desta função. Sabemos que o gráfico de uma função quadrática é uma parábola. Para a função lucro determinada, temos os seguintes valores para as constantes, a, b e c, respectivamente, -1, 9 e -20.

Como a = -1<0, a parábola possui concavidade voltada para baixo;
O ponto de vértice é:
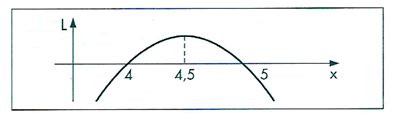
Portanto o ponto x que maximiza a função lucro é x = 4,5.

Vamos ver se você acompanhou o nosso raciocínio...E qual será o lucro máximo?

Resposta.

Veja um esboço do gráfico da função lucro..... Observe que, neste caso, o lucro só é positivo, para valores de x variando entre 4 e 5. Ou seja, para qualquer quantidade fora deste intervalo o proprietário está tendo prejuízo. Por isso, a importância de se saber estudar o sinal de uma função, determinando quando a mesma é positiva ou negativa...