Módulo 2 - Taxa Nominal, Efetiva, Unificada e Over

Por outro lado, sabemos que o montante final (FV2) pode ser calculado mediante a aplicação de uma taxa única, resultado da unificação das duas taxas que compõe a operação (iu), então, FV2 pode ser dado também pela seguinte equação:

FV₂=PV(1+i_u)

(3)

Substituindo-se a equação (2) na (3), tem-se:

FV1(1+i2)=PV(1+iu)

(4)

Substituindo-se a equação (1) na (4), obteremos:

PV(1+i₁)(1+i₂)=PV(1+i_u)

(5)

Simplificando a equação (5) e resolvendo para (iu), encontraremos:

iu=(1+i₁)x(1+i₂)-1

(6)

A fórmula (6) representa a taxa unificada (iu) de uma operação envolvendo duas taxas. Conforme podemos notar, iu ≠ i1 + i2.

Se desejássemos unificar “n” taxas, teríamos:

iu=(1+i₁)x(1+i₂)x...x(1+i_n)-1

(7)

A fórmula (7) poderia ser representada, ainda, pela seguinte equação:

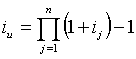(8)

Onde representa o “produtório” das taxas “j”, da 1ª até n-ésima taxa que compõem o problema.

Exemplo

Sabendo-se que a taxa referencial (TR) para a próxima sexta-feira é de 0,6273%, qual será a remuneração de uma conta de poupança (rendimento de 0,5%a.m + TR) com aniversário naquela data?

Dados	Solução
i1 = TR = 0,006273	iu=(1+i₁)x(1+i₂)x...x(1+i_n)-1
i2 = 0,005	iu=(1+0,006273)x(1+0,005)-1
	i_u=0,011304 ou i_u=1,1304%

R: A remuneração da poupança será de 1,1304%.

Note que o resultado é diferente da soma das taxas!