Ativo A:        cv = 0,04272/0,165
                   cv = 0,2589

Ativo B:        cv = 0,056789/0,165
                   cv = 0,3442

O Ativo B opera com um coeficiente de variação mais alto; logo, é mais arriscado que o Ativo A.

Observe a razão: 0,3442/0,2589 = 1,3295; isto significa que o Ativo B é 1,3295 vez mais arriscado que o Ativo A.

10) Partindo da hipótese de que a distribuição de probabilidade de retornos para os Ativos A e B (exemplo 8) é normal, calcule a faixa de resultados dos retornos esperados associados com as seguintes probabilidades de ocorrência: a)68,26%; b)95,46%; c) 99,74%.

Resposta

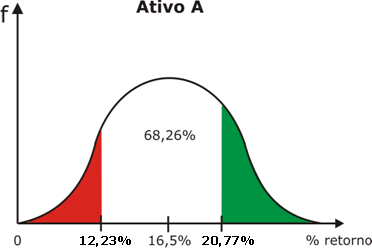
Ativo A

a) 68,26% do retorno esperado irão localizar-se entre:

16,5% - 4,272% = 12,228%
16,5% + 4,272% = 20,772%

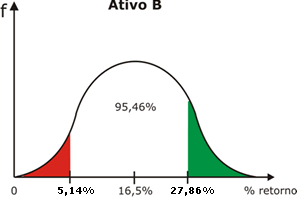
b) 95,46% do retorno esperado irão localizar-se entre:

16,5% - (4,272% x2) = 7,956%
16,5% + (4,272% x2) = 25,044%

c) 99,74% do retorno esperado irão localizar-se entre:

16,5% - (4,272% x3) = 3,684%
16,5% + (4,272% x 3) = 29,316%

Ativo B

a) 68,26% do retorno esperado irão localizar-se entre:

16,5% - 5,6789% = 10,8211%
16,5% + 5,6789% = 22,1789%

b) 95,46% do retorno esperado irão localizar-se entre:

10,8211% - 5,6789% = 5,1422%
22,1789% + 5,6789% = 27,8578%

c) 99,74% do retorno esperado irão localizar-se entre:

5,1422% - 5,6789% = -0,5367%
27,8578% + 5,6789% = 33,5367%