Resolução 2
Esse exemplo poderá
ser operado com base na seguinte equação extraída
de Gitman (2004, p. 280)
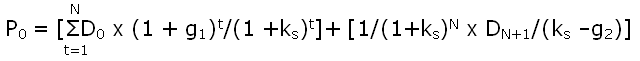
Onde:
P0 = Valor corrente da ação ou valor estimado
ou valor teórico ou ainda valor intrínseco da ação
D0 = dividendo atual
DN+1= dividendo do primeiro período de crescimento constante
t = período de taxa de inicial
g1= taxa de crescimento inicial
ks= taxa de desconto = custo da ação ordinária
= taxa de retorno exigida pelo investidor = taxa de corte
N = período de crescimento constante (perpétuo)
g2= taxa de crescimento constante (perpétuo)
Nesse exemplo temos:
ks= 16%
D0 = $1,15
T = 5
g1= 10%
g2= 6%
N = 5
DN+1 = $1,96321169 (será apurado no desenvolvimento
do exemplo)
a) P0 = [∑D0 x (1 + g1)t/(1
+ks)t]
Os dividendos atuais: D0 = $1,15/ação
Dividendos com crescimento de 10% ao ano
D1 = $1,15 x (1,10)1 = $1,265
D2 = $1,15 x (1,10)2 = $1,3915
D3 = $1,15 x (1,10)3 = $1,53065
D4 = $1,15 x (1,10)4 = $1,683715
D5 = $1,15 x (1,10)5 = $1,8520865
O valor presente dos
dividendos esperados nos cinco primeiros anos atinge o seguinte valor:
P0 = $1,265/1,161 + $1,3915/1,162 + $1,53065/1,163
+1,683715/1,164 + $1,8520865/1,165
P0 = $ 4,91695438
b) P0 =
[1/(1+ks)N x DN+1/(ks–g2)]
Os dividendos que se iniciam no ano 6 atingem a:
D6 = $1,8520865 x (1,06)1 = $1,96321169
D7 = $1,8520865 x (1,06)2 = $2,081004391
D8 = $1,8520865 x (1,06)3 = $2,205864655
E assim por diante.
O valor presente desses
dividendos é obtido no ano 5. Para transferir esse valor para o
ano 0 (momento atual), deve-se atualizá-lo pelo fator: (1,16)5,
ou seja:
P0 = [$1,96321169/(0,16 – 0,06)]/(1,16)5
P0 = $19,6321169/2,100341658
P0 = $9,347106374
Vamos agora operar
a segunda parte da equação pela fórmula:
P0 = 1/(1+0,16)5 x $1,96321169/(0,16 – 0,06)
P0 = 0,476113015 x $19,6321169
P0 = $9,347106374
Logo, o valor presente
do total dos dividendos no momento 0, que representa o valor teórico
da ação, atinge a:
c) P0 = [SD0 x (1 + g1)t/(1
+ks)t]+ [1/(1+ks)N x DN+1/(ks–g2)]
P0 = $ 4,91695438 + $9,347106374
P0 = $14,26406075 por ação