Unidade 01 - Matemática Básica

Associatividade

a+(b+c)=(a+b)+c e a.(b.c)=(a.b).c

Em outras palavras, não importa a ordem que se somem três parcelas ou multiplique três fatores, o resultado será o sempre o mesmo.
De fato, a associatividade é válida para expressões com mais termos e não apenas com três termos.
Devido à associatividade podemos suprimir os parênteses em certas expressões.

Exemplo:
	3+(2+5)=(3+2)+5=3+2+5 7.(3.4)=(7.3).4=7.3.4 21.(9.x)=(21.9).x=189x

Distributividade

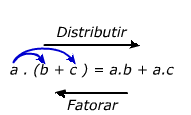
A distributiva relaciona as operações de multiplicação e de adição conjuntamente, nela se encontra a explicação de como multiplicar um termo por uma soma com dois ou mais termos ou, como transformar uma soma de duas multiplicações em uma multiplicação com uma soma. Confuso?! Para simplificar a distributividade nos permite, além de distribuir, fatorar (colocar em evidência).

Exemplo:

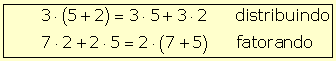Operações com Expressões Algébricas...

- Adição e Subtração

Podemos simplificar uma expressão algébrica agrupando os termos semelhantes; somando algebricamente os coeficientes numéricos e mantendo a parte literal ou algébrica.

Exemplo: 2x + 5x – 2y –y = 7x -3y

- Multiplicação e Divisão

Para encontrarmos o produto (ou quociente) de dois ou mais monômios precisamos calcular o produto (ou quociente) de seus coeficientes numéricos e das partes literais, aplicando, sempre que possível, a propriedade do produto (ou quociente) de potências de mesma base.

Exemplo: 2xy(x²-2y) = x³y-4xy²

- Potenciação

Basta aplicar a propriedade da potência de uma potência para calcularmos a potência de um monômio.

Exemplo: (3x²y³)² = 9x⁴y⁶

Quando a expressão em questão possuir apenas números, as regras apresentadas não são muito empregadas. Utilizamos as regras acima para resolver expressões em que precisamos determinar o valor de uma variável. O que será exposto em seguida.