3 - Resolvendo Equações do 2o grau
Uma equação
do segundo grau é uma equação da forma ax2+bx+c=0,
onde a, b e c são números reais com
a![]() 0.
0.
| Exemplo: | |
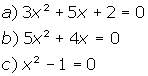 |
|
Existe um algoritmo para resolver uma equação do segundo grau (encontrar os valores para x que satisfazem a igualdade), tal algoritmo recebe o nome de Fórmula de Báskhara e diz que uma equação do segundo grau pode possuir no máximo duas soluções reais determinadas pelas fórmulas:
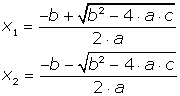
A
expressão dentro do radical recebe o nome de discriminante e é
representado pela letra grega maiúscula ![]() (delta),
assim:
(delta),
assim:
|
|
| x1 e x2 recebem o nome de raízes da equação do segundo grau. |
| Exemplo:
Encontre as soluções das equações do segundo grau (encontre as raízes) a seguir: |
|
| a) x2-3x+2=0 | |
| Resolução: | |
| Temos que a=1 b=-3 e c=2 e pelas fórmulas de Baskhara, obtemos: | |
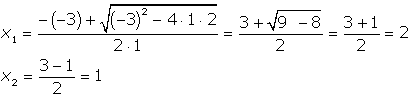 |
|
| Logo o conjunto solução da equação é {1,2}. Observe neste exemplo que D=1 >0 e que obtivemos duas raízes reais e distintas. |
| b) x2-2x+1=0 Resolução: |
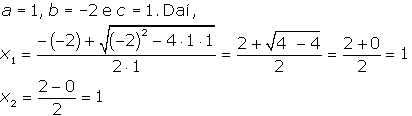 |
| Neste exemplo, as duas raízes são iguais a 1. Observe que D=0 |
|
c)
3x2+3x+1=0 |
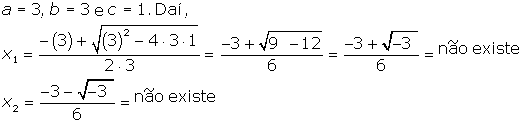 |
| Neste exemplo, as duas raízes não existem. Observe que D<0. |
Em geral uma equação do segundo grau ax2+bx+c=0 pode ser escrita como um produto de fatores de 1o grau, se a equação possuir raízes reais, da seguinte forma:
![]()
| Exemplo: | |
| a)
A equação x2-3x+2= (x-1)(x-2)
=0 b) A equação x2-2x+1= (x-1)(x-1) = (x-1)2 =0 c) Não é possível fatorar 3x2+3x+1 pois a mesma não possui raízes reais. |
|
