Considere f(x)=2x+1 onde o domínio de f(x) é A={1,2,3,4} e o contra-domínio é B = R. Para construir o gráfico de f(x) precisamos encontrar os valores do contra-domínio que estão associados com os elementos do domínio, esses elementos do contra-domínio recebem o nome de imagem de x por f(x). Costuma-se fazer uma tabela com os valores, como a seguir:

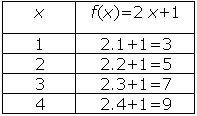
Marcamos os elementos do domínio num eixo horizontal e os elementos do contra-domínio num eixo vertical, os dois eixos se interceptando no ponto (0,0) dito origem do sistema (ou do plano cartesiano).

Em seguida traçamos retas cortando o eixo x verticalmente em 1, 2, 3 e 4 (os valores do domínio de f), o mesmo se faz no eixo y, só que agora serão retas horizontais em 3, 5, 7, 9 (as imagens dos elementos do domínio) quando a reta que passa pelo valor do domínio interceptar a reta que passa pela respectiva imagem obtemos um ponto do gráfico da função.

Veja a figura:

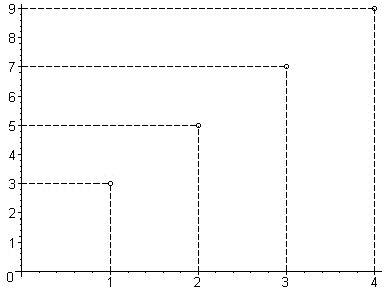
O domínio da função anterior era finito logo colocamos apenas quatro pontos, mas se o domínio fosse, por exemplo, todos números reais entre 0 e 4, incluindo o zero e o quatro, teríamos que marcar infinitos pontos em ambos os eixos e depois encontrar os pontos de interseções das retas horizontais e verticais, e isso seria inviável. Então como devemos proceder?

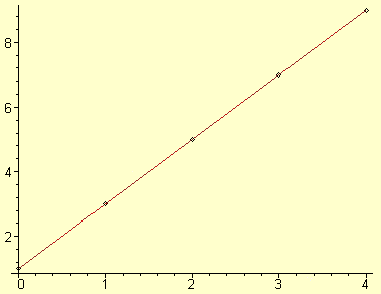
Na verdade não conseguimos fazer uma representação precisa para todo tipo de uma função quando o domínio é infinito, conseguimos apenas uma aproximação, mas tal aproximação nos fornece uma interpretação gráfica suficiente para entendermos o comportamento da função. Vejamos como proceder com a função acima para x percorrendo todos os reais entre 0 e 4, incluindo o zero e o quatro.
Fazemos, inicialmente uma tabela, com alguns pontos do domínio dado, escolheremos 0, 1, 2, 3 e 4., depois calculamos sua respectiva imagem.

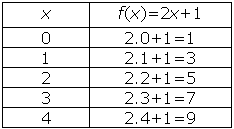
Em seguida, marcamos os pontos no plano cartesiano.

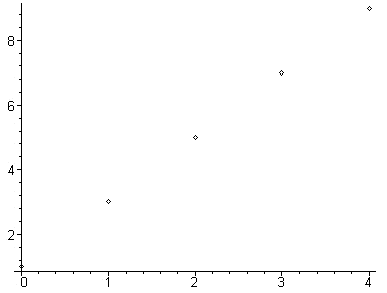
Agora unimos os pontos por uma linha suave, obtendo a seguinte figura.

Viu como é fácil?! Vamos complicar um pouco mais?!