a) Se x unidades são vendidas durante o primeiro ano, expresse a função lucro como função de x.
b) Estima-se que 23.000 unidades serão vendidas durante o primeiro ano. Use o resultado da parte (a) para determinar o lucro do primeiro ano se os dados de venda forem atingidos.
c) Determine o ponto de nivelamento.
Resolução:
a) O problema nos fornece os seguintes dados:
x = número
de unidades vendidas
Custo fixo = 140.000,00;
Custo variável = 25,00 por unidade;
Preço de venda = 65.
Para obter a função lucro é necessário que se conheçam as funções receita e custo.
Assim, Receita = 65.x e o custo total será C(x) = 140.000 + 25x
Logo, o Lucro = L(x) = 65x-(25x+140.000) = 65x-25x-140.000 = 40x-140.000
L(x) = 40x-140.000
b) Se x = 23.000 então neste exemplo queremos determinar L(23.000), (isto é feito substituindo o valor de x por 23.000 na equação do lucro).
Portanto,
L(23.000) = 40(23.000)-140.000 = 780.000
Assim, caso ele venda 23.000 unidades obterá um lucro de R$ 780.000,00.
c) No ponto de nivelamento o lucro é nulo, portanto, R(x) = C(x).
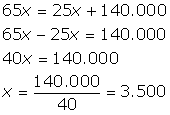
Assim, quando o fabricante vender 3500 unidades terá lucro nulo, ou seja, não perde mas também não ganha.
Procure resolver o exercício...
O custo mensal
fixo de uma fábrica que produz esquis é R$ 4.200, e o custo
variável é de R$ 55,00 por par de esquis. O preço
de venda é R$105,00 por par de esquis. Se x pares de esquis são
vendidos durante o mês expresse o lucro mensal como função
de x.
a) 40x-1500
b) 50x-4200
c) 3200
d) 3x-3900
e) 40x-4000
Resposta.