Imagine
que X representa o número de rádios a serem produzidos e
Y, o número de gravadores. O objetivo de Maximizar o lucro pode
ser representado por uma combinação de X e Y. Como o lucro
obtido em cada x é de $ 200, podemos expressar a contribuição
potencial de x como lucro X = 200x; do mesmo modo o lucro potencial em
cada gravador pode ser expresso por lucro Y = 500y.
A função que maximiza o lucro da produção
dos dois itens pode ser expressa como:
Maximizar 200x + 500y
Agora que já se sabe que a intenção é Maximizar
lucros, temos que conhecer as restrições à produção:
- só
temos 40 transistores por dia e eles são utilizados na produção
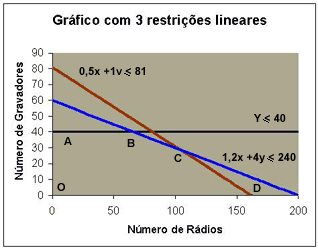
de Gravadores, logo: y <
40
- tempo
destinado à produção dos dois itens não
pode superar 240 horas por dia. Sabendo-se que cada rádio (x)
consome 1,2 hora e cada gravador (y), 4 horas, a restrição
pode ser mostrada como: 1,2x + 4y <
240
- tempo de inspeção dos dois itens não pode superar 81 horas por dia. Sabendo-se que cada rádio (x) consome 0,5 hora e cada gravador (y), 1 hora, a restrição pode ser expressa como: 0,5x + 1y < 81
A restrição final refere-se ao fato de que o número de itens produzidos não pode ser inferior a zero: x, y > 0.
Representação do modelo completo