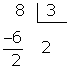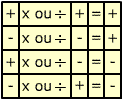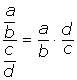Nesta seção procuraremos revisar algumas operações aritméticas básicas. Sugerimos, mesmo se o conceito parecer muito fácil, que sejam feitos todos os exercícios da seção.
Adição e Subtração - Somar e subtrair é muito fácil, não é?! Esperamos que sim. Nesta subseção trataremos de somar e subtrair números inteiros e números racionais (números em forma de frações).
Somar
dois números positivos, qualquer pessoa sabe, não
sabe? |
||
| Por exemplo, 5+7=12, 4594+798=5392. | ||
Existe até
mesmo um dispositivo prático para somar dois números, que
pode ser utilizado não apenas para somar números, mas também
para somar expressões (mas isto é uma outra história).
Para efetuar 4594+798, utilizando o dispositivo, escrevemos os números
da seguinte forma:
![]()
Soma-se da
direita para a esquerda. No caso acima, se soma primeiro 4 com 8, obtendo
12, escreve-se o 2 abaixo do 8 e leva-se o 1 do 12 para cima do 9, soma-se
agora o 1 com o 9 obtendo 10 e depois com o outro 9, obtendo 19, coloca-se
o nove abaixo do 9, sobe-se o 1 e assim por diante.
Muito fácil, não é? A complicação começa
quando os números têm sinais diferentes. Nesta hora recomendamos
que seja feita uma associação com saldo bancário,
número com sinal positivo significa crédito e número
com sinal negativo significa débito.
Se nos deparamos com a seguinte conta 2-3, dizemos que temos um crédito
de 2 e um débito de 3, então nosso saldo será um
débito 1, ou seja, saldo igual a -1.
Notação: Os termos envolvidos em uma adição recebem o nome de parcelas e o resultado da adição de dois números recebe o nome de soma.
A regra geral é:
|
|
Veja os exemplos:
a) 2 + 3 = 5
b) (-3) + (-4) = -7
c) (-5) + (3) = -2
d) (-3) + (7) = 4
e) (-2) + (5) + (-4) = -1
Na subtração a coisa não muda tanto. Na verdade podemos encarar uma subtração como uma soma. Por exemplo, 5 – 4 = 5 + (-4) = 1. Entendeu? É só utilizar as regras da adição. Outro exemplo: (-2) – (-5) = (-2) + (5) = 3. De uma forma geral,
|
Veja os exemplos:
a) (-20) – (30)
= (-20) + (-30) = -50
b) 13 – (-18) = 13 + (18) = 31
c) (-12) – (5) – (-38) = (-12) + (-5) + (38) = 21
Se desejar,
vá para a clínica
e faça mais exercícios.
Fica aqui um desafio que utiliza operações com inteiros.
Desafio:
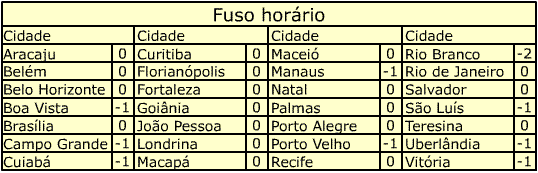
Quando são
16 horas em Cuiabá, que horas são:
a) em Salvador?
b) em Rio Branco?
c) em Manaus?


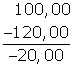
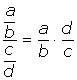
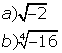
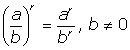
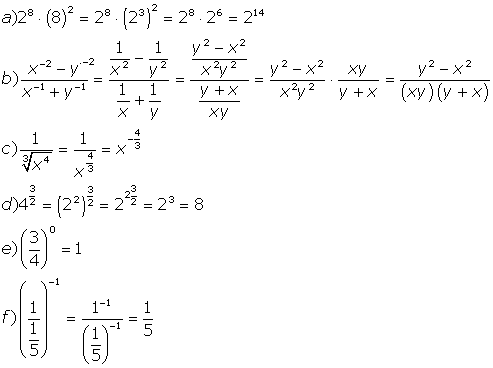
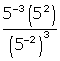
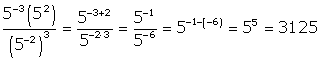
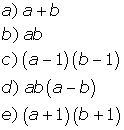
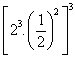 ?
?
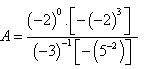 na forma de um número inteiro?
na forma de um número inteiro?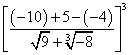 ?
? 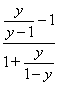 é igual a:
é igual a: 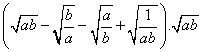 e sabendo que a e b são números reais maiores que zero,
obtemos:
e sabendo que a e b são números reais maiores que zero,
obtemos: