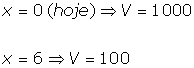1 - Estudo das funções

Ocorrem muitos casos, na prática, onde o valor de uma quantidade depende do valor de outra. Assim o salário de uma pessoa pode depender do número de horas trabalhadas, o número de unidades de certo produto demandado pelos consumidores pode depender de seu preço, a produção total numa fábrica pode depender de máquinas utilizadas, e assim por diante. A noção matemática que contempla os exemplos citados anteriormente (e milhares de outros), é a definição de função. Vejamos a definição de função.

Sendo A e B conjuntos, uma função de A em B é uma correspondência que a cada elemento x (variável) de A associa um único elemento y de B. A é chamado de domínio da função e B é chamado de imagem da função.

Utilizamos a notação y = f(x) para representar a regra que associará a cada elemento x do domínio, a um único elemento y do conjunto imagem. Como x é livre para variar no domínio da função, diz-se que x é a variável independente, e que y, por depender de x, é a variável dependente.

A seguir veremos alguns exemplos numéricos de como podemos operar com uma relação funcional.

a) Seja f a função tendo por domínio o intervalo A = [0,1], definida por f(x)=x³. Então f é a correspondência que a cada x do intervalo A = [0,1] associa o número y=x³. Dessa forma, vamos calcular os valores de y = f(x) para alguns valores de x pertencente ao domínio A.

Quando x = 0 : y = f(0) = 0³ = 0
Quando x = 1/2 : f(1/2) = (1/2)³ = 1/8

Podemos observar que x é transformado em y pela relação f(x) = x³.

É importante ressaltar, que apenas a regra que usamos para associar os elementos não define uma função. É necessário ter, pelo menos, uma noção dos conjuntos, domínio e imagem, envolvidos pela tal regra.

Por exemplo, considere uma função definida pela regra Será que conseguimos associar o número x = 0 a um valor correspondente y? Ou seja, existe o valor de f(0)? Obviamente não, pois não existe divisão por zero e f(0) seria 1/0. Neste caso, dizemos que o domínio desta função são todos os número reais, com x 0. Entendeu?

Vamos a mais um exemplo:

Considere a função f(x) = Qual seria o domínio desta função? Ou seja, esta função tem alguma restrição para que exista? Tem sim... O denominador não pode ser zero, então para que essa condição seja satisfeita x 4. Concorda? Logo, dizemos que o domínio desta função será todos os números reais, com x 4.

E se a função for f(x) = , qual o seu domínio? Será que esta função tem alguma restrição de existência? x pode ser igual a 0? Não, pois não existe . Assim, o radicando x - 2 0, então x 2, que é o domínio da função.

Dada a função f(x) = 2x-1 então será:

a) 1 b) 4 c)2/7 d) 3 e) 2

Resposta:

Dada encontre .

a) 3 b) 8/3 c) 2 d) 4 e) 0

Resposta:

Exemplo 01:

Na produção de um determinado produto, uma empresa tem um custo fixo de R$400,00 mais um custo variável de R$10,00 por cada produto. Apenas com as informações dadas obtenha a função que represente o custo total da empresa.

Resolução:

Ora, o custo da empresa depende da quantidade de produtos que ela produz. Seja x a quantidade de produtos que a empresa produz e seja C o custo total da empresa na produção dos produtos. Daí,

C(x)=400+10x

Observação:

Utilizamos letras que tenham a ver com o contexto. Trataremos custo por C, lucro por L, receita por R e assim por diante.
Lembrando que o importante não é a letra que utilizamos e sim o que ela representa. Se a letra escolhida facilitar a nossa compreensão do assunto, melhor.

Exemplo 02:

Se voltarmos ao problema anterior e perguntarmos: qual o custo da empresa se 50 produtos forem produzidos? Como resolver este problema?

Resolução:

Alguns alunos poderão mentalmente encontrar a resposta para a pergunta, procedendo de forma parecida com a seguinte:

Cada produto custa R$10, eu adquiri 50, então o custo será de 50.10=500 mais ainda tem o custo fixo de R$400,00 o que perfaz R$900,00.

Usando a expressão da resolução do exemplo anterior, podemos proceder de outra forma:
Como x representa a quantidade de produtos produzidos então substituiremos x por 50 na expressão do custo, vejamos

Logo,

C(50)=400+10(50)=900

A leitura da expressão acima é: 'O custo para adquirir 50 produtos é de R$900,00'.

Vejamos um exemplo mais complicado, só que agora começaremos a omitir passagens.

Exemplo 03:

Um operário que chega ao trabalho às 8 horas da manhã, terá produzido p(x)=-x³+6x²+15x rádios transistores x horas mais tarde.

a) Quantas rádios terá produzido às 10 horas da manhã?
b) Quantos rádios terá produzido entre 11 e 12 horas?

Neste problema muitos devem ter pensado:'Ora, basta substituir o x por 10 na equação. E pensaram errado!
Para quem teve este pensamento, e para quem sequer entendeu o problema, recomendamos mais uma lida no enunciado do exemplo.
Observe que a variável x no problema representa horas após as 8. Logo, devemos substituir x por 2 na equação e não por 10.

Resolução:

Logo às 10 horas (2 horas após as oito) o trabalhador terá montado 46 rádios transistores.

Como proceder no item b)?

Exercícios

1) O domínio da função real é o conjunto:
	a) { x Î R / x ³ 1}
	b) R*
	c) { x Î R / x > 1}
	d) R -{1}
	e) nda
	Resposta:

2) Qual dos gráficos abaixo não representa uma função?
	a)
	b)
	c)
	d)
	e)
	Resposta:

3) O domínio de é:
	a) R+
	b) R*
	c) R
	d) { x Î R / x ¹ 2}
	e) { x Î R / x ¹ ±2}
	Resposta:

4) O domínio da função real de variável real definida por . Qual dos conjuntos seguintes representa um domínio para f?
	a) { x Î R / x ³ 0}
	b) { x Î R / -1 < x < 0}
	c) { x Î R / x < -1 ou x > 1}
	d) { x Î R / x ¹ ±1}
	e) { x Î R / x ³ 0 e x ¹ 1}
	Resposta:

5) O domínio da função real é?
	a) { x Î R / x ¹ 7}
	b) { x Î R / x ³ 2}
	c) { x Î R / x ³ 2 e x ¹ 7}
	d) { x Î R / x ¹ 2}
	e) { x Î R / x ³ 0 e x ¹ 1}
	Resposta:

Exercícios

6) Das figuras abaixo a única que representa o gráfico de uma função real y=f(x) é:
	a)
	b)
	c)
	d)
	e)
	Resposta:

7) Dado com , x¹0 é igual a:
	a)
	b)
	c)
	d)
	e)
	Resposta:

8) O domínio da função f definida por é:
	a)
	b)
	c)
	d)
	e)
	Resposta:

9) Qual dos diagramas seguintes representa uma função de A em B?
	a)
	b)
	c)
	d)
	e)
	Resposta:

Exercícios

11) Das figuras abaixo a única que representa o gráfico de uma função real y=f(x), é
	a)
	b)
	c)
	d)
	e)
	Resposta:

12) Seja f a função definida de R em R definida por:
	a)
	b)
	c)
	d)
	e) nda
	Resposta:

14) O domínio da função definida por é :
	a) {x Î R|-1£ x £ 1 e x¹0}
	b) R
	c) {x Î R|-1£ x £ 1}
	d) {x Î R|-1< x < 1 e x¹0}
	e) {x Î R|x < 1}
	Resposta:

15) O mais amplo domínio real da função definida por é:
	a) R
	b) ]-¥, 2[È[3,+¥[
	c) [3,+¥[
	d) ]-¥, 2[
	e) ]2,3]
	Resposta:

Exercícios

16) O domínio da função é o conjunto dos números reais tal que:
	a) x £ -3 ou x > 2
	b) x < -2 ou x ³ 3
	c) -2 £ x £ 3
	d) -3 £ x £ 2
	e) x > -2
	Resposta:

17) O domínio da função real é
	a)
	b)
	c)
	d)
	e) nda
	Resposta:

18) Seja f a função de R em R definida por f(x)=x2-3x+4. Calcule :
	a)
	b)
	c)
	d)
	e) nda
	Resposta:

2 - Representação Gráfica

Existe um provérbio Chinês que diz que uma figura vale mais do que mil palavras. Isto se aplica muito em matemática. No caso de funções a representação de seu gráfico, é a figura que vale mais do que mil palavras.

Definição: O gráfico de uma função f é o conjunto dos pares ordenados (x, f(x) ), para qualquer x pertencente ao domínio de f.

Representação Gráfica de uma Função.

Uma grande utilidade da matemática para o curso de administração será aprender a interpretar gráficos. Podemos a partir de um gráfico encontrar a função que o representa de melhor forma e tendo a função podemos obter o seu gráfico. Mas o que vem a ser um gráfico?

A resposta para esta pergunta será dada a seguir, antes vejamos o que você conhece de gráfico, onde você já viu um gráfico. Muitas notícias mostradas em jornais, revistas e telejornais utilizam gráficos para ilustrar a notícia.

A grande maioria das pessoas consegue compreender o que o gráfico está tentando 'dizer'. Isto é, a informação fica melhor compreendida com a ajuda do gráfico.

Muitas vezes teremos em mão uma regra de uma função que diz respeito, por exemplo, a produtividade de uma empresa e queremos visualizar melhor o que aquela regra está nos dizendo, nessas horas o gráfico fornecerá muito mais informações de forma que várias pessoas possam entender. Como qualquer pessoa com um conhecimento mínimo de matemática consegue compreender facilmente vários tipos de gráficos, isto pode ajudar e muito quando, por exemplo, da apresentação de um plano de negócios para investidores potenciais, ou ainda, da apresentação do seu produto para prováveis compradores e as aplicações seriam muitas, além é claro de aumentar o seu conhecimento.

Um gráfico de um função f(x) é o conjunto de pares ordenados (x, f(x)) onde x percorre o domínio e f(x) percorre o contra-domínio de f(x).

Representar pares ordenados é muito fácil. Não é?

A melhor forma de entendermos o que vem a ser um gráfico de função será dando exemplos. Começaremos com exemplos simples e depois complicaremos gradativamente.

Considere f(x)=2x+1 onde o domínio de f(x) é A={1,2,3,4} e o contra-domínio é B = R. Para construir o gráfico de f(x) precisamos encontrar os valores do contra-domínio que estão associados com os elementos do domínio, esses elementos do contra-domínio recebem o nome de imagem de x por f(x). Costuma-se fazer uma tabela com os valores, como a seguir:

Marcamos os elementos do domínio num eixo horizontal e os elementos do contra-domínio num eixo vertical, os dois eixos se interceptando no ponto (0,0) dito origem do sistema (ou do plano cartesiano).

Em seguida traçamos retas cortando o eixo x verticalmente em 1, 2, 3 e 4 (os valores do domínio de f), o mesmo se faz no eixo y, só que agora serão retas horizontais em 3, 5, 7, 9 (as imagens dos elementos do domínio) quando a reta que passa pelo valor do domínio interceptar a reta que passa pela respectiva imagem obtemos um ponto do gráfico da função.

Veja a figura:

O domínio da função anterior era finito logo colocamos apenas quatro pontos, mas se o domínio fosse, por exemplo, todos números reais entre 0 e 4, incluindo o zero e o quatro, teríamos que marcar infinitos pontos em ambos os eixos e depois encontrar os pontos de interseções das retas horizontais e verticais, e isso seria inviável. Então como devemos proceder?

Na verdade não conseguimos fazer uma representação precisa para todo tipo de uma função quando o domínio é infinito, conseguimos apenas uma aproximação, mas tal aproximação nos fornece uma interpretação gráfica suficiente para entendermos o comportamento da função. Vejamos como proceder com a função acima para x percorrendo todos os reais entre 0 e 4, incluindo o zero e o quatro.
Fazemos, inicialmente uma tabela, com alguns pontos do domínio dado, escolheremos 0, 1, 2, 3 e 4., depois calculamos sua respectiva imagem.

Em seguida, marcamos os pontos no plano cartesiano.

Agora unimos os pontos por uma linha suave, obtendo a seguinte figura.

Viu como é fácil?! Vamos complicar um pouco mais?!

Agora considere que a função dada seja f(x)=-x³+6x²+15x com domínio R.
Faremos novamente uma tabela com valores pertencentes ao domínio de f e calculamos a imagem.

Marcando os pontos obtidos na tabela no plano cartesiano, obtemos.

Unindo os pontos, obtemos:

Se introduzirmos mais pontos teremos:

Quanto mais pontos introduzirmos teremos uma idéia melhor de como a função se comporta. O gráfico ficaria parecido com o seguinte:

Repassando o que foi visto.

Para esboçar o gráfico de uma função por marcação de pontos quando o domínio é infinito siga os seguintes passos:
- Calcule o valor de f(x) para uma quantidade representativa de elementos do domínio de f. (tabela);
- Marque os pontos obtidos no item anterior no plano cartesiano;
- Una os pontos por uma curva suave e pronto.

Vamos considerar agora a função f(x)=x³+5x²+3x+7.Calculando os valores para. Obtemos a seguinte aproximação do gráfico de f(x).

Começamos, construindo a tabela:

Em seguida, marcamos os pontos no plano cartesiano:

Em seguida unimos os pontos por uma linha suave.

Entendido!!

Talvez este gráfico fosse bem representativo de um problema em que a variável x não pudesse ser negativa. Mas e se a variável x pudesse ser negativa? Não teríamos idéia do comportamento da função. Na verdade o gráfico da função acima toma valores bem interessantes para valores negativos de x, vejamos.
Vamos considerar agora que x Î {-3,-2,-1,0,1,2,3,4} ou seja acrescentamos três valores negativos ao conjunto tomado anteriormente.
Marcando os pontos obtidos no plano cartesiano e unindo por uma linha suave. teríamos:

Observe então que a escolha dos pontos que marcaremos no plano cartesiano é fundamental na hora da construção do esboço do gráfico de uma função.

Quando possuímos a regra de uma função e queremos saber se um ponto pertence ao gráfico da função substituímos as coordenadas do ponto da regra da função e verificamos se obtemos uma identidade. Confuso?! Vejamos em exemplos.

Exemplo:

Verifique se o ponto (2,5), pertence ou não ao gráfico da função, f(x)=9x²+3x-1.

Resolução:

A resolução é muito simples, um ponto sempre é formado por duas coordenadas, a primeira é dita abscissas e pertence ao domínio da função (variável independente), a segunda é dita ordenada e pertence ao contra-domínio da função (variável dependente), então para o ponto dado, (2,5), o 2 representa o x e o 5 representa o f. Substituímos o x por 2 e o f(x) por 5 na regra e vejamos o que se obtém:

O que não é verdade nunca, logo o ponto (2,5) não pertence ao gráfico da função.

Exemplo:

Verifique, agora, se o ponto (1,11) pertence ou não ao gráfico da função do exemplo anterior.

Resolução:

O que é verdadeiro, logo o ponto (1,11) pertence ao gráfico da função f(x)=9x²+3x-1.

Sinal de uma função

Quando se pergunta qual o sinal de uma função estamos preocupados em determinar os valores do domínio onde a imagem é negativa, ou positiva, ou zero. Quando temos em mãos o gráfico da função e queremos determinar o sinal da função basta verificar os intervalos em que o gráfico da função está acima ou abaixo do eixo x.

Exemplo:

Determine o sinal da função cujo gráfico é dado a seguir:

Resolução:

A função é positiva para x entre -1 e 2 e para x maior que 3, e é negativa para x menor que -1 e para x entre 2 e 3.
Podemos colocar o sinal no próprio gráfico para facilitar a identificação

Raízes de uma função

As raízes de uma função são os elementos do domínio cuja imagem é zero. Ou seja, são os valores de x onde o gráfico da função intercepta o eixo das abscissa (o eixo x).

Exemplo:

Considerando o gráfico do exemplo anterior, determine as raízes da função.

Resolução:

Neste caso as raízes da função são os valores x=-1, x=2 e x=3.

Interceptos do gráfico de uma função

Com o próprio nome sugere, interceptos são pontos onde o gráfico da função intercepta os eixos do plano cartesiano. Os interceptos x, são também ditos raízes da função (visto anteriormente). O intercepto y, não têm um nome especial, mas são mais fáceis de serem determinados quando temos a regra da função. Basta, para isto, substituir o valor de x por 0 e pronto.

Exemplo:

Encontre os intercepto y para a função do exemplo anterior.

Resolução:

O intercepto y será o ponto (0,6), e uma função só pode ter no máximo um intercepto y.

Exercícios

2) Estude o sinal da seguinte função de R em R, :
	a)
	b)
	c)
	d)
	e) nda
	Resposta:

3) Estude o sinal da função f(x)=(2x-1)2-(2x+2)2-3.
	a)
	b)
	c)
	d)
	e) nda
	Resposta:

4) Estude o sinal de h(x) cujo gráfico está representado abaixo e marque a opção correta.
	a)
	b)
	c)
	d)
	e) nda
	Resposta:

5) Seja f: R® R uma função tal que f(3x+1)=1-x, então f(a) é:
	a) 1-a
	b) -3a
	c) 3a+1
	d)
	e) 4-3a
	Resposta:

Exercícios

7) A imagem da função f: R® R, definida por , contém o elemento:
	a) -2
	b) 0
	c)
	d) 2
	e) 5
	Resposta:

3 - Plano cartesiano

Podemos representar geometricamente os números reais numa reta: a cada ponto da reta corresponde um número real, e cada número real corresponde um ponto na reta.

Podemos também representar pares ordenados de números reais pelos pontos de um plano em que fixamos um sistema de coordenadas (ou plano cartesiano) formado por duas retas que se interceptam perpendicularmente, dispostas como na figura a seguir:

Para representar o par (3,2), que chamaremos de ponto A, procedemos assim:

• Partindo do zero, caminhamos 3 unidades no eixo dos x, para a direita;
• daí, caminhamos 2 unidades paralelamente ao eixo dos y, para cima.

O par (-2,-1 ) é representado no ponto B, assim obtido:

• Partindo do zero, caminhamos 2 unidades no eixo dos x, para a esquerda;
• daí, caminhamos 1 unidade paralelamente ao eixo y, para baixo.

Nomenclatura

Eixo x= eixo das abscissas
Eixo y= eixo das ordenadas
Ponto O, onde representamos (0,0), é a origem do sistema de coordenadas o plano cartesiano.
Ponto A, onde representamos (3,2), é o ponto de coordenadas (3,2); a primeira coordenada, 3, é a abscissa de A; a segunda coordenada, 2, é a ordenada de A.
Os eixos x e y dividem o plano em quatro regiões denominada quadrantes e numeradas como na figura.
O ponto A está no 1º quadrante; E está no 2º quadrante; B está no 3º quadrante; F está no 4º quadrante.

2 - Funções lineares ou do 1º grau

É toda função do tipo y=mx+b, onde m e b são contantes reais e m 0. Ou se preferir, f(x)=mx+b.

São exemplos de funções lineares:

a) f(x)=3x+4
b) f(x)=100x
c) g(x)=7
d) y=2

Vale salientar que os exemplos c) e d) são funções denominadas constantes, vistas anteriormente, que são casos particulares das funções lineares, quando m = 0.

a) Coeficientes m e b da função linear

A constante b é denominada coeficiente linear e, graficamente, representa a ordenada do ponto de interseção da reta com o eixo y, tendo coordenadas (0, b).

O coeficiente m é denominado coeficiente angular da reta ou inclinação da reta. Não entraremos em detalhes aqui, mas a inclinação de uma reta é justamente a tangente do ângulo formado pelo eixo x e a reta, medida no sentido anti-horário a partir do eixo x. Para entender melhor o assunto, precisaríamos de um certo conhecimento de trigonometria e isto não foi visto.

b) As raízes de uma função linear.

A raiz de uma função é o valor de x para o qual a função se anula. Graficamente, a raiz é representada pela abscissa do ponto de intersecção da reta com o eixo x. Dessa forma, devemos encontrar x tal que f(x) =0 . Logo,

y = mx+b = 0 x= -

Observe que se m = 0 e b 0, a função não possui raiz real, pois não existe divisão por zero. Mas, se m = b = 0, a função possui infinitas raízes, pois a função passaria ser 0. x = 0 e a solução dessa equação é qualquer número x pertencente aos reais.

c) O gráfico de uma função linear.

Como o próprio nome já diz trata-se de uma função cujo gráfico é uma reta, podendo ser obtido a partir de dois pontos. Você já ouviu dizer que dois pontos distintos determinam uma única reta? Pois é, isso é a pura verdade.

Vamos esboçar a gráfico da função y=2x+1...

É necessário lembrar que o gráfico de uma função é o conjunto de pontos ou pares ordenados (x, f(x)). Logo, como se trata de uma função linear, cujo gráfico é uma reta, precisamos encontrar pelo menos 2 pontos pertencentes a este conjunto. Assim, atribuindo a x os valores 0 e 1, obtemos os valores de y correspondentes, através da regra da função em estudo . Lembre-se que os valores de x são independentes, logo podem assumir qualquer valor no domínio da função, a escolha é arbitrária.

Marcando os dois pontos obtidos (0, 1) e (1, 3) no plano cartesiano obtém-se o gráfico da reta descrita pela função y=2x+1.

Observe que o gráfico intercepta o eixo y exatamente no valor do coeficiente b da função, ponto (0, 1), e que a raiz é o ponto de intersecção do gráfico com o eixo x, representada pelo ponto (-1/2,0).

Exemplos: Esboce o gráfico das funções:
a) y=5
b) y=-5x+6

Resposta:

a)

Vamos obter a equação da reta y=mx+b que passa pelos pontos Q(x1, y1) e P(x2, y2).

1º Passo) Conhecendo-se dois pontos pertencentes à reta o coeficiente angular m pode ser calculado, através da relação:

m = =

2º Passo) Para calcular o coeficiente linear b, deve-se substituir na equação geral da reta (y=mx+b), o valor de m, calculado anteriormente, e (x, y) por um dos pontos P ou Q, previamente conhecidos.

Com os coeficientes m e b determinados, a expressão geral pode ser escrita para quaisquer (x, y) pertencente à reta. Ficou confuso? Vamos praticar.....

Exemplo: Vamos obter a equação da reta y=mx+b que passa pelos pontos (-2, 7) e (1, 1).

1º Passo: Determinar o coeficiente angular m.

m = m = = = -2 (cuidado com os sinais)

2º Passo: Substituir o valor de m e um dos pontos conhecidos, na equação geral da reta y=mx+b, para encontrar o valor da constante b.

Vale salientar que a escolha do ponto a ser substituído é indiferente e que a equação obtida com qualquer um deles deve ser mesma.

Vamos utilizar o ponto (-2, 7).... Assim, vamos fazer x = -2, y = 7 e m = -2, para encontrar o b.

y = mx+b 7= -2.(-2) +b 7= 4+b b = 3

Assim, para m = -2 e b = 3, temos que a equação da reta que passa por estes 2 pontos é dada por: y=-2x + 3.

Exemplos: Determinar a equação da reta que passa pelos pontos:

a) (2, 3) e (5, -3)
b) (0,-4) e (-2, -7)

Resposta:

a)

b)

Se m é positivo então a função será crescente e terá o aspecto mostrado na Fig.(a). Se m é negativo então é decrescente e terá o aspecto mostrado na Fig. (b).

Observe que à direita e a esquerda da raiz da função, há uma mudança de sinal, ou seja, a função (o valor de y) passa de positivo para negativo ou vice-versa. Assim, funções crescentes são positivas a direita da raiz e negativas à esquerda. Já as decrescentes, são positivas a esquerda da raiz e negativas á direita.

Veja mais alguns exercícios de fixação da matéria.

Exercícios

2) Qual dos gráficos abaixo representa a seguinte função :
	a)
	b)
	c )
	d)
	e) nda
	Resposta:

4) Seja uma função linear. Sabe-se que e . O valor de é:
	a) 0
	b) 3
	c) 13
	d) 23
	e) 33
	Resposta:

5) Se f(x)=ax+b, e então o valor de a é:
	a) 1
	b) 2
	c) 3
	d) 4
	e) nda
	Resposta:

8) O gráfico que representa a função definida por é:
	a)
	b)
	c)
	d)
	e) nda
	Resposta:

9) Para a função f de em , definida por , é :
	a) -4
	b) 2
	c) 5
	d) -10
	e) nda
	Resposta:

10) Para a função f de em , definida por , então é igual a:
	a) 1
	b) -1
	c) -2
	d) 8
	e) nda
	Resposta:

Exercícios

15) Qual dos gráficos abaixo representa a seguinte função .
	a)
	b)
	c)
	d)
	e) nda
	Resposta:

Função do 2º grau (Parábola)

Uma função do segundo grau é uma função cuja expressão é um polinômio de grau dois.
Ou seja, uma função da forma , com .

As funções a seguir são exemplos de funções do segundo grau.
Exemplo:

Vamos construir o gráfico de uma função do segundo grau por marcação de pontos.

Exemplo:
Obtenha o gráfico da função .

Resolução:

Comecemos construindo a tabela com valores.

Agora, marcando os pontos no plano cartesiano e unindo por uma curva suave, obtemos

A curva vem descendo e parece que a partir de x=2 ela começara a subir. Vamos jogar mais dois pontos para verificar se isso acontece de verdade.

Na verdade o gráfico de qualquer função do segundo grau terá um comportamento parecido com a função do exemplo acima, esta curva recebe o nome de parábola. Os valores onde o gráfico intercepta o eixo x (das abscissas) recebem o nome de raízes do gráfico da função, justamente onde a imagem se anula, o ponto de mínimo ou de máximo do gráfico da função recebe o nome de vértice da função.

Para esboçar o gráfico de uma função do segundo grau nos concentraremos em determinar apenas quatro pontos no máximo: o vértice, as raízes (no máximo duas), e o intercepto y.
Para encontrar as raízes procedemos como no caso de polinômio do segundo grau, utilizamos a fórmula de Báskhara. Logo

Onde a,b e c são os coeficientes do polinômio.
Para encontrar as coordenadas do vértice da parábola, utilizamos as seguintes equações

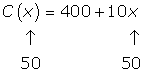
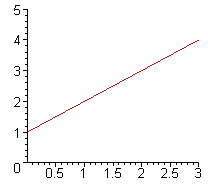
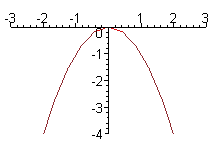
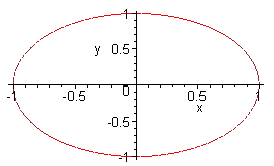
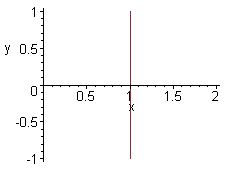
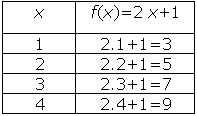
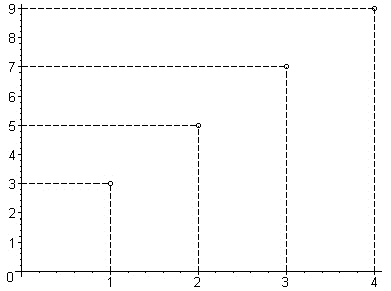
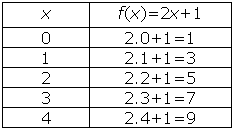
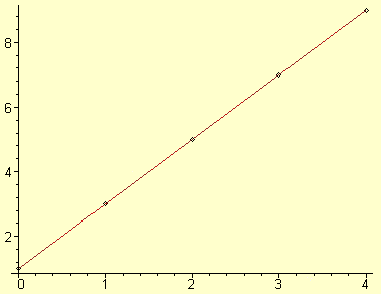
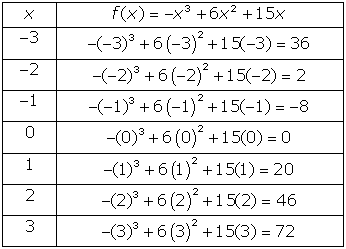
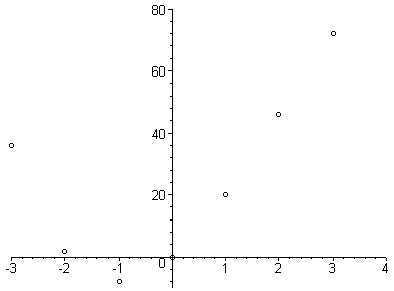
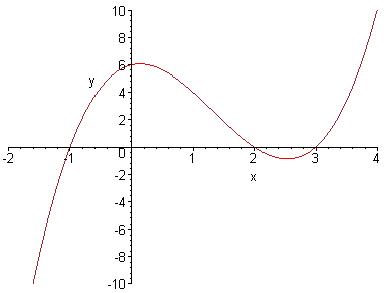
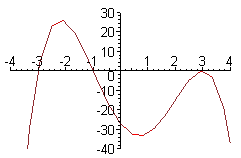
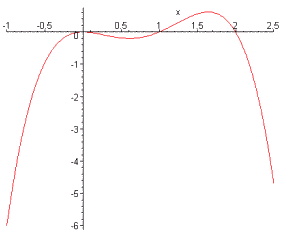
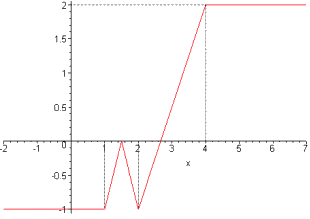
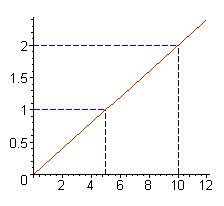
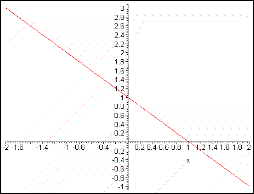
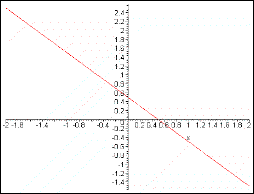
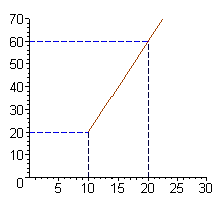
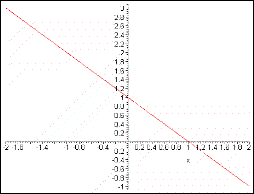
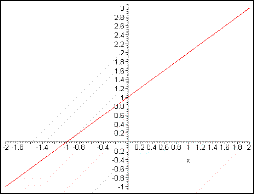
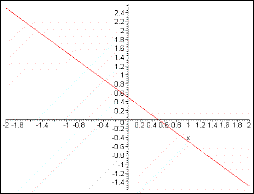
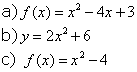
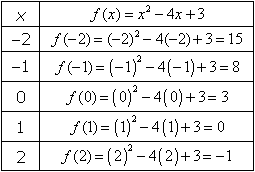
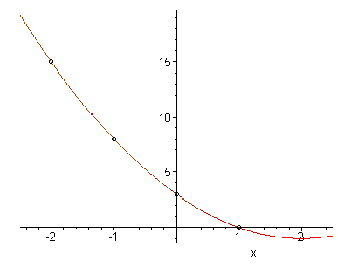
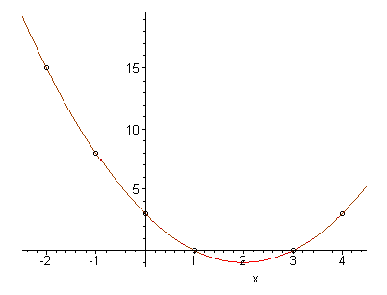
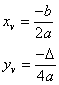
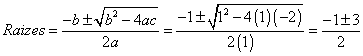
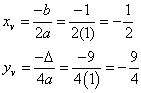
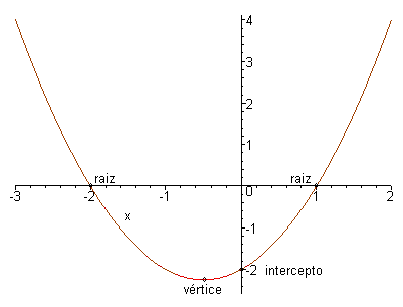
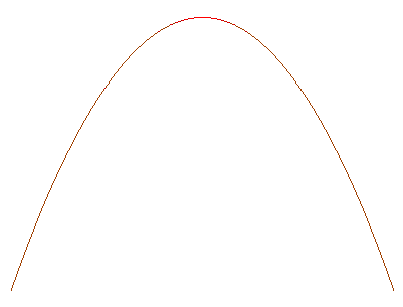
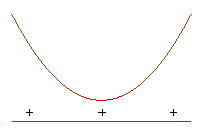
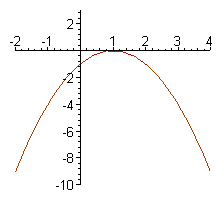
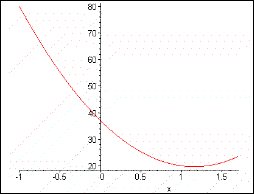
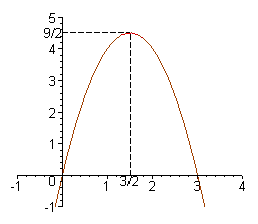
O intercepto y, é o ponto onde x=0, para determinar tal ponto basta, portanto, substituir x por zero na função e encontraremos o termos independente c. Logo o intercepto y é o ponto (0,c).

Exemplo:
Esboce o gráfico da função .

Resolução:
Utilizaremos então apenas os quatro pontos mencionados acima.
Comecemos pelas raízes da equação. Temos que a=1, b=1e c = -2.

Logo x= -2 e x=1 são as raízes do gráfico da função.

Passemos ao vértice da parábola.

Lembre-se de que

Falta agora o intercepto y, que é o ponto .
Marcando estes pontos no plano cartesiano, obtemos o seguinte gráfico.

Podemos ter gráficos voltados para baixo, como o esboço a seguir

O que determina se a função será voltada para baixo ou para cima é o sinal de a. Se a é negativo o gráfico da função é voltado para baixo, e dizemos, neste caso, que o gráfico da função tem concavidade voltada para baixo. Se a é positivo o gráfico da função é voltado para cima, e dizemos, neste caso, que o gráfico da função tem concavidade voltada para cima.

O sinal de uma função quadrática
Se e , teremos uma parábola com concavidade voltada para cima com duas raízes, e o sinal seria dado por

Se e teremos uma parábola com concavidade voltada para baixo com duas raízes, e o sinal seria dado por

Se e teremos uma parábola com concavidade voltada para cima com uma raiz real dupla, e o sinal seria dado por

Se e , teremos uma parábola com concavidade voltada para baixo com uma raiz real dupla, e o sinal seria dado por

Se e , teremos uma parábola com concavidade voltada para baixo sem raízes reais, e o sinal seria dado por

Se e , teremos uma parábola com concavidade voltada para baixo sem raízes reais, e o sinal seria dado por

Exemplo:
Estude o sinal de

Resolução:

Temos que e a função possui duas raízes -1 e 4. Temos, também, que . Logo o sinal de f(x) é

Exercícios

1) Qual gráfico corresponde à seguinte função :
	a)
	b)
	c)
	d)
	e) nda
	Resposta:

2) Que gráfico representa a função :
	a)
	b)
	c )
	d)
	e) nda
	Resposta:

3) Determine o vértice da parábola e assinale a opção correta:
	a)
	b)
	c)
	d)
	e) nda
	Resposta:

4) Qual é o vértice da seguinte parábola :
	a)
	b)
	c)
	d)
	e) nda
	Resposta:

5) Determine o valor de m na função real para que o valor mínimo seja :
	a) 1
	b) -1
	c) 2
	d) -2
	e) nda
	Resposta:

6) Qual é a função cujo gráfico está representado ao lado:
	a)
	b)
	c)
	d)
	e) nda
	Resposta:

8) Estude o sinal da seguinte função quadrática e assinale a opção correta:
	a)
	b)
	c)
	d)
	e) nda
	Resposta:

9) Estude o sinal da seguinte função quadrática e assinale a opção em que a função assume valores positivos:
	a)
	b)
	c)
	d)
	e) nda
	Resposta:

10) A função possui como raízes os números 2 e 4, e seu gráfico é uma parábola com vértice (3, -3).O valor de a+b+c é:
	a) 3
	b) 6
	c) 9
	d) 12
	e) 15
	Resposta:

Exercícios

11) Se a equação não tem raízes reais, é verdade que:
	a)
	b)
	c)
	d)
	e)
	Resposta:

12) O gráfico ao lado representa uma função quadrática: Essa função é: :
	a)
	b)
	c )
	d)
	e)
	Resposta:

13) Se m e n são raízes de ,então o valor de vale:
	a) 6
	b) 2
	c) 1
	d)
	e)
	Resposta:

14) Seja 7 a diferença entre as raízes da equação . Então, o valor da constante c é:
	a) -24
	b) -20
	c) -16
	d) -4
	e) 5
	Resposta:

15) As raízes da função quadrática são positivas e uma é o dobro da outra. A soma dessas raízes é:
	a) 2,4
	b) 2,1
	c) 1,8
	d) 1,5
	e) 1,2
	Resposta:

16) Observe a figura: Nessa figura, a parábola de vértice V é o gráfico de . Sendo AO=2(OV) e a abscissa de V diferente de zero, o valor de c é:
	a) 0
	b)
	c)
	d) 1
	e) 4
	Resposta:

17) O gráfico de uma função está representado ao abaixo. Podemos afirmar que:
	a)
	b)
	c)
	d)
	e)
	Resposta:

18) O domínio da função definida por é o conjunto dos números reais x, tal que:
	a)
	b)
	c)
	d)
	e)
	Resposta:

19) O domínio da função é o conjunto:
	a) ] -1,4[
	b)
	c)
	d)
	e)
	Resposta:

2 - Função Receita

Seja x a quantidade de produtos vendidos ao preço p. A receita de uma empresa é a arrecadação total que se tem pela venda de um determinado produto. Logo, a função receita é definida como sendo:

R(x) = p . x

Exemplo 02: Suponha que o preço de comercialização de camiseta do exemplo anterior seja de RS 7,00. Determine a função receita.

Se o preço é p = 7,00, então se x unidades são vendidas, a receita total arrecadada é de 7.x.
Ou seja, R(x) = 7 . x

3 - Função Lucro

A função lucro é definida como sendo a diferença entre as funções, receita e custo. Assim, supondo que as quantidades produzidas e comercializadas sejam iguais a x, o lucro total envolvido é dado por:

L(x) = R(x) - C(x)

Exemplo 03: Vamos obter a função lucro para o nosso exemplo da malharia que vem sendo desenvolvido, cujas funções custo e receita, foram C(x) = 2 . x +100 e R(x) = 7 . x, respectivamente.

L(x) = R(x) - C(x) L(x) = 7x - (2 . x +100)

L(x) = 5x - 100

A partir da definição da função lucro dada, pode-se concluir que:

Se R(x) > C(x) Lucro é positivo.
Se R(x) < C(x) Lucro é negativo, ou seja, prejuízo
Se R(x) = C(x) Lucro é nulo

Observe que o gráfico da função custo parte do valor do custo fixo, pois quando a produção é zero, a empresa terá que pagar o custo fixo independente da produção. Já a função receita, parte da origem (0,0), pois quando não se comercializar nenhuma unidade, certamente a arrecadação ou receita obtida também será nula.

Analisando o gráfico acima podemos fazer as seguintes interpretações:

- Para quantidades x maiores que 20, a receita é maior que o custo, o que implica em um lucro maior que zero (positivo).

- Para quantidades x menores que 20, a receita é menor que o custo, o que implica em um lucro menor que zero (negativo), portanto, prejuízo.

- Para x = 20 unidades as duas retas se interceptam quando x = 20 unidades, o que significa que para x = 20 a receita é igual ao custo e, portanto, o lucro é zero. Para quantidades x menores que 20, a receita é menor que o custo

As mesmas conclusões podem ser feitas ser feitas se analisarmos o gráfico da função lucro abaixo.

De uma forma geral, o valor de x para o qual o lucro é nulo é chamado de ponto de nivelamento ou break-even point e é obtido fazendo R(x) = C(x) ou L(x) = 0

Observações:

i) A diferença entre o preço de venda e o custo variável por unidade é chamada de margem de contribuição por unidade. Representa o lucro parcial obtido por cada unidade vendida.

= p -

ii) Chama-se custo médio de produção ou custo unitário (x), a relação entre o custo total C(x) e a quantidade x, isto é, = . De forma análoga, pode-se obter a receita média (x) ou qualquer outra função média.

x = número de unidades vendidas
Custo fixo = 140.000,00;
Custo variável = 25,00 por unidade;
Preço de venda = 65.

Para obter a função lucro é necessário que se conheçam as funções receita e custo.

Assim, Receita = 65.x e o custo total será C(x) = 140.000 + 25x

Logo, o Lucro = L(x) = 65x-(25x+140.000) = 65x-25x-140.000 = 40x-140.000

L(x) = 40x-140.000

b) Se x = 23.000 então neste exemplo queremos determinar L(23.000), (isto é feito substituindo o valor de x por 23.000 na equação do lucro).

Portanto,

L(23.000) = 40(23.000)-140.000 = 780.000

Assim, caso ele venda 23.000 unidades obterá um lucro de R$ 780.000,00.

c) No ponto de nivelamento o lucro é nulo, portanto, R(x) = C(x).

Assim, quando o fabricante vender 3500 unidades terá lucro nulo, ou seja, não perde mas também não ganha.

Procure resolver o exercício...

O custo mensal fixo de uma fábrica que produz esquis é R$ 4.200, e o custo variável é de R$ 55,00 por par de esquis. O preço de venda é R$105,00 por par de esquis. Se x pares de esquis são vendidos durante o mês expresse o lucro mensal como função de x.

a) 40x-1500
b) 50x-4200
c) 3200
d) 3x-3900
e) 40x-4000

Resposta.

Entendidas as funções demanda e oferta, vamos explicar o conceito de ponto de equilíbrio de mercado......

O ponto de equilíbrio de mercado é o ponto de intersecção entre a curva de oferta e de demanda. Observe, no gráfico abaixo, que neste ponto os preços dados pelas funções, oferta e demanda, são iguais, assim como as quantidades ofertadas e demandas. Neste caso, haverá um preço e uma quantidade de equilíbrio.

Observe que a função oferta é crescente, pois quanto maior o preço maior será a quantidade que ofertada pelo produtor. Já a função demanda é decrescente, pois quanto maior o preço menor será a quantidade procurada pelo consumidor.

O nome ponto de equilíbrio de mercado decorre do seguinte fato:

Se Quantidade ofertada é maior que a demandada. Logo, excesso de oferta, provoca queda de preço.

Se Quantidade demandada é maior que a ofertada. Logo, excesso de demanda, provoca aumento de preço.

Exemplo 03

Considere a função demanda e oferta por sorvetes, dadas por: p=10–0,002x e , respectivamente. Determine o preço de equilíbrio de mercado.

Resolução:

No ponto de equilíbrio de mercado o preço, dado pelas funções demanda e oferta são iguais. Então para obter o ponto de equilíbrio, é necessário impor estar igualdade. Logo,

(Para facilitar, vamos multiplicar toda a equação por 3500)

Assim, a quantidade de equilíbrio é x = 3500 unidades e o preço correspondente é obtido substituindo esta quantidade em uma das funções, oferta ou demanda. Logo, o preço de equilíbrio será:

p = 10 - 0,002 . 3500 = R$ 3,00

Veja ilustração do problema no gráfico abaixo:

a) Vamos inicialmente esboçar o gráfico da função que descreverá a depreciação da máquina com o passar do tempo. Estamos considerando que a depreciação é linear, logo o gráfico é uma reta. Seja x tempo e V o valor da máquina.

Observe que quando:
Daí temos dois pontos P1=(0,1000) e P2= (6,100)
Temos então o seguinte gráfico: