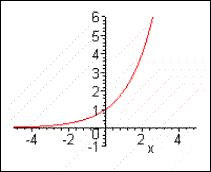
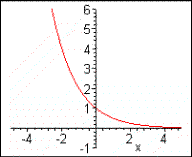
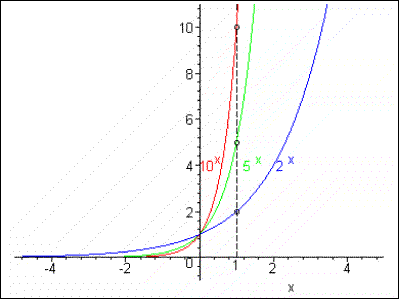
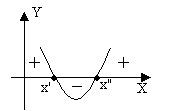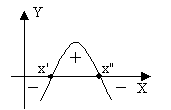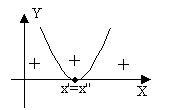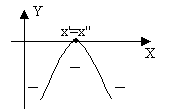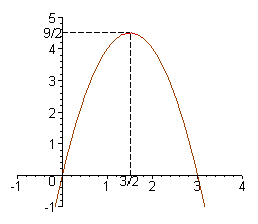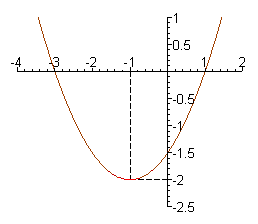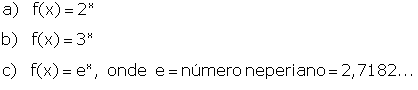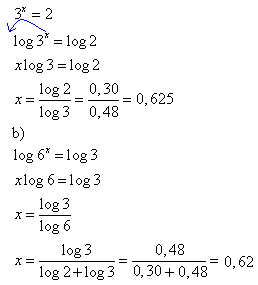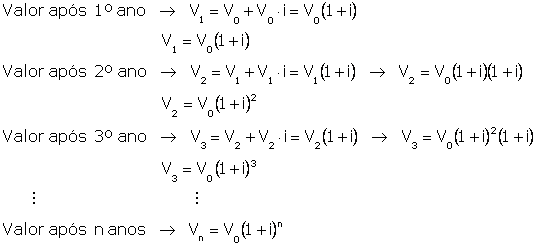| Este mesmo
raciocínio e expressão pode ser aplicado à problemas
de crescimento populacional, valorização e desvalorização.
Haverá uma pequena diferença na notação, pois
trabalharemos com taxa de crescimento da população em vez
de juros, população inicial em vez de capital inicial e
população em vez de montante. Já no caso da desvalorização,
observa-se que aparecerá uma subtração e, isto faz
sentido, pois como a taxa sempre toma valores entre 0 e 1 teremos, desta
forma, que (1- i) será um número menor que 1 e, portanto,
a função decrescerá com o passar do tempo, por isso
o nome desvalorização.
De uma forma
geral, seja uma grandeza V que varia exponencialmente com tempo n, a uma
taxa i, por unidade de tempo. Suponha que no instante inicial seu valor
seja V0 e nos instantes 1, 2, 3, ..., n, os valores sejam V1, V2, V3,
..., Vn. Dessa forma, o valor da grandeza V no instante n é dado
por:
V = V0
(1±i)n  
Observações:
- Para utilizar
a relação acima descrita, a unidade do tempo n deve ser
compatível com a taxa i. Por exemplo, se i é a taxa de juros
por ano, n representa o número de anos; se i é a taxa por
bimestre, n corresponde ao número de bimestres, etc.
- Na relação acima, o sinal de (+) é utilizado para
problemas de crescimento e o sinal (-) para problemas de decrescimento.
Exemplo:
O número
de habitantes de uma cidade é hoje 7.000, e cresce à taxa
de 3% ao ano.
a) Qual será o número de habitantes daqui a 8 anos?
b) Qual será o número de habitantes daqui a 30 anos?
c) Daqui a quanto tempo (aproximadamente) a população dobrará?
Resolução:
a) 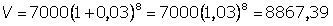
Daqui a 8 anos a população será de 8867 habitantes.
b) 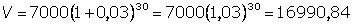
Daqui a 30 anos a população será de 16991 habitantes.
c)

Daqui a aproximadamente
23 anos e 6 meses a população dobrará. |
![]() 0.
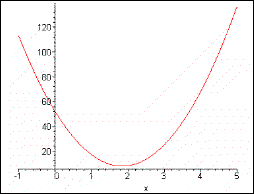
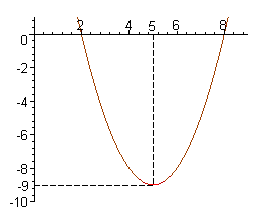
Ou, simplesmente, uma função polinomial de grau 2.
0.
Ou, simplesmente, uma função polinomial de grau 2. ![]()
![]()
![]()
![]()