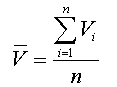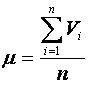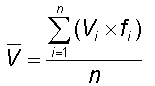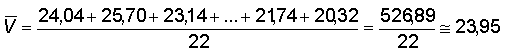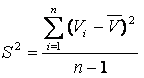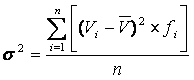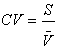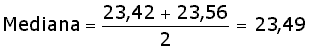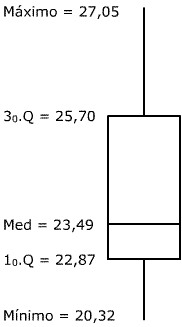1 - Utilizando a Estatística

Relatamos quatro situações que ocorrem em diferentes contextos e para as quais os recursos estatísticos podem ser utilizados de forma a dar grande contribuição, seja para: estruturação de uma pesquisa e análise dos dados levantados; acompanhamento e relacionamento de valores de natureza econômica; interpretação de medidas até certo ponto "populares" (como é o caso de renda per capita e expectativa de vida, que são duas médias, do ponto de vista estatístico).

1 - A área de recursos humanos de uma empresa deseja implementar uma pesquisa de clima organizacional (satisfação dos empregados) para posterior elaboração de um "plano de retenção de talentos".

Como fazer? O que medir ou avaliar? Quantos empregados entrevistar? Como selecioná-los?

2 - Uma determinada instituição financeira tem recebido, por meio de sua ouvidoria - serviço de atendimento ao cliente - sucessivas reclamações de clientes que alegam estar esperando muito tempo antes do início do atendimento nas agências. Deve ser elaborado um diagnóstico que forneça subsídios a uma possível elaboração de um plano de ação para melhoria do atendimento.

O que deve ser medido? Como? Deve-se incluir todas as agências ou não? Em caso negativo, quais devem ser incluídas no estudo? Que medidas devem ser tomadas e em quais dias da semana? Em quais horários? Os clientes devem ser entrevistados? Em caso afirmativo, como selecioná-los e o que perguntar.

3 - Considere que você esteja "tentado" a investir no mercado de ações e decida acompanhar a performance de um conjunto de empresas, na bolsa de valores, por um determinado período de tem po, antes de tomar uma decisão sobre investir ou não.

Quais as melhores alternativas para acompanhamento dos valores/variações diárias nas cotações das ações das diferentes empresas sob análise?

É possível comparar/relacionar a performance das ações de uma determinada companhia com aquela divulgada diariamente para a Bolsa como um todo?

4 - Acaba de ser divulgado um estudo informando o resultado da renda per capita brasileira no último ano e também da expectativa de vida de homens e mulheres em nosso país.

O que significam exatamente estes valores?

Como interpretá-los de forma adequada?

Seriam necessárias medidas estatísticas complementares para permitir um melhor entendimento da renda per capita e da expectativa de vida?

Quais e por quê?

2 - E a Estatística?

Embora os censos sejam uma "manifestação" bastante concreta e familiar da Estatística, há muitas outras possibilidades de estudos contemplados por esta área do conhecimento. Convém lembrar que, mesmo com aplicações históricas que datam de milênios, como as já apresentadas, o termo, tal como hoje é conhecido, só surgiu na literatura em meados do século XVIII.

Assim podemos entender Estatística como:

Como grandes áreas ou funções da Estatística, temos:

3 - Coletando Dados

Tendo em vista que os dados constituem a matéria prima da Estatística, a fim de viabilizar estudos dos mais diferentes fenômenos e de variáveis a eles associadas, é muito importante que sua coleta seja feita da forma mais adequada, sendo que há duas formas básicas pelas quais eles podem ser obtidos:

O uso de dados secundários deve levar em conta se os mesmos são compatíveis com o objetivo pretendido.

O autor também ressalta que os títulos das publicações e as definições podem ser bastante limitados ou, então, tecnicamente corretos no sentido usado por técnicos, porém por ninguém mais. Os resultados podem omitir fatos importantes ou incluir estimativas e o método de compilação pode ter sido modificado, prejudicando comparações com resultados publicados anteriormente.

Os dados secundários podem ser classificados em três, segundo Mick Silver:

Dados Primários - A coleta de dados é uma etapa muito delicada da pesquisa. Deve ser feita com muito cuidado e de preferência pelo próprio pesquisador. Repassar essa atividade para terceiros pode levar a coletas distantes do que realmente estamos pesquisando. Vejamos um exemplo de Mick Silver (2000) para pesquisa de uma população.

4 - O Mau Uso da Estatística

"Distorções on-line"

As estatísticas brasileiras devem ser lidas com cuidado. Tome-se um exemplo no campo do e-commerce, a venda de produtos pela internet. Segundo dados da GM, dirigida por José Carlos Pinheiro Neto, 80% dos carros Celta são vendidos on-line. Ocorre que a maior parte dessas transações é fechada nas concessionárias. Motivo: os vendedores orientam o comprador a usar a internet na loja mesmo, porque há desconto para a compra via computador." Revista Veja, edição 1728, de 28 de novembro de 2001, página 34, seção Holofote.

Este pequeno comentário contém uma séria advertência sobre a utilização absolutamente distorcida de estatísticas (como já definido anteriormente), chama nossa atenção para que sejamos criteriosos e procuremos buscar a validação da base de dados disponível e fazer a leitura correta de quaisquer indicadores que nos sejam apresentados.

Resumo

Foi apresentada uma breve "localização" histórica de levantamentos estatísticos (com destaque para os censos), mostrando que, a despeito de conceitos teóricos, a necessidade de dispor de dados confiáveis a respeito de determinados fenômenos, de uma população (ou universo) e algumas de suas características (ou variáveis), sempre se fez presente na história, desde anos anteriores ao nascimento de Cristo.

Os conceitos introdutórios de Estatística incluem variáveis (quantitativas e qualitativas), censo e amostragem, universo / população (todos os indivíduos ou objetos) e amostra (uma parte do universo). Suas grandes áreas ou funções são Estatística Descritiva, Probabilidade e Inferência.

Estatísticas dizem respeito a conjuntos numéricos (taxas, índices/indicadores) vinculados a determinados fenômenos (econômicos, sociais, demográficos).

A coleta de dados pode ser feita via dados secundários, já disponíveis como fruto da coleta de outra pessoa, grupo ou organização (que incluem estatísticas oficiais, estatísticas não oficiais e estatísticas obtidas dentro de empresas) ou primários (que são coletados pelo pesquisador/instituição que conduz o estudo e podem ser obtidos por observação, experimentação, entrevistas - com ou sem aplicação de um questionário formal, fontes de documentação disponibilizadas por algumas organizações).

Deve-se ter especial cuidado com o mau uso (inadequado ou distorcido) da Estatística, sendo necessário um estado de alerta para que ela não seja utilizada para manipulação de dados, no mau sentido, para "legitimar" premissas inconsistentes ou induzir, deliberadamente, interpretações equivocadas o que, definitivamente, não é um papel ao qual ela se preste.

1 - Medidas Estatísticas

A análise descritiva busca, com a utilização de algumas medidas estatísticas, sintetizar um conjunto de dados (sejam esses amostrais ou populacionais), permitindo uma compreensão satisfatória de seu comportamento (de sua distribuição) ou, em outras palavras, oferecendo uma efetiva descrição da base de dados disponível.

Passamos agora a descrever um conjunto de dados que não esteja agrupado, ou seja, cada valor da base é apresentado "individualmente", de forma que pode ser identificado claramente.

Exemplo:

Considere que a empresa para a qual você trabalha solicita que você acompanhe a cotação da ação de uma determinada Companhia (Companhia C) na Bolsa de Valores de São Paulo ao longo de um mês (22 dias úteis). Diligentemente você faz isto e ao final daquele mês você tem os seguintes dados (em reais, o lote de 1000 ações):

24,04; 25,70; 23,14; 22,87; 23,42; 23,96; 25,69; 26,78; 26,88; 27,05; 27,05; 26,12; 24,60; 23,56; 23,04; 21,30; 21,75; 21,85; 22,89; 23,14; 21,74; 20,32.

Ao final do período de observação você deve dar uma breve descrição do comportamento das cotações daquela Companhia, para seu supervisor, permitindo uma visualização minimamente consistente da situação.

Deixando de lado algumas verdades (tais como: o mercado acionário é bastante complexo, com muitas variáveis subjetivas envolvidas – "humor" dos investidores, suas incertezas e seus receios – ou que, diante da natureza da variável em questão, o tempo para observação pode ser insuficiente), e tendo como preocupação prestar uma informação com valor e que seja mais que a apresentação dos 22 valores numéricos acompanhada de um gráfico, o que pode ser dito?

O significado das medidas que serão apresentadas em seguida valem tanto para dados não agrupados (tais como os exemplificados) como para dados agrupados.

2 - A Média

A média tem feito parte do nosso cotidiano com certa regularidade, afinal, todos nós já fomos confrontados ou submetidos a "notas médias", "salários médios", "pesos médios", "alturas médias" ou outros resultados do gênero.

Sua obtenção é simples, pois basta que sejam somados todos os valores correspondentes a todos os dados disponíveis e esta soma seja dividida pela quantidade de dados. Esta definição é válida para média aritmética simples.

De modo mais formal, se utilizarmos o exemplo anterior e dissermos que a variável cotação do lote de ações da Companhia C será denotada por V (representando a variável valores) e considerando ainda que essa base de dados é amostral, a cotação média será:

onde:

é o valor médio das cotações do lote de ações ao longo do mês.

corresponde ao valor de cada cotação observada a partir do  primeiro dia do mês (i = 1) até o último (i = n = 22).

é a quantidade de dados observados, neste caso o número de  cotações diárias, ou seja 22.

Entretanto, se tivéssemos trabalhando com uma base de dados populacionais, o símbolo da média não seria mais o nome da variável com uma barra em cima, mas sim a letra grega µ. Assim, a formulação matemática para a determinação da média para dados populacionais seria dada por:

Por outro lado, considerando o fato de que alguns dados podem se repetir e representando por f_i o número de repetições, ou frequência, de cada valor dentro da base de dados, chegaríamos, para uma base de dados amostrais, por exemplo, a uma formulação genérica como:

O que significa dizer que um aluno concluiu seu curso com nota média de 7,5 (numa escala de zero a dez), após concluir as 20, 30 ou 40 disciplinas do currículo?

Ou ainda, o que significa dizer, dentro daquela mesma ótica, que uma turma de 45 alunos teve nota média de 6,4 (também em uma escala de zero a dez) em um exame de Estatística?

Por último, como deveríamos entender quando um noticiário da televisão divulga resultado de um recente estudo, de um órgão internacional respeitadíssimo, dizendo que a renda por habitante no ano passado em um determinado país é de US$ 8.900,00 (que nada mais é que uma renda média por habitante)?

Seria razoável supor que todos os valores de uma base de dados (ou pelo menos a maioria deles) são suficientemente próximos do valor médio? Se, "por obra do acaso", metade de uma turma tira nota máxima (dez) em um exame na faculdade e a outra metade nota mínima (zero), a conclusão é que a nota média é cinco, o que não reflete proximidade dos valores originais com esta média. Claro que este é um caso extremo, mas útil para que despertemos para esta questão do uso indiscriminado de médias.

O exemplo anterior (nota mínima zero, nota máxima dez e nota média cinco) poderia induzir-nos a acreditar que média é o valor que está "no meio" (ou pelo menos muito próximo a ele), entre o mínimo e o máximo. Seria isto verdade?

Suponhamos que um estudante faça quatro provas com pesos iguais e tire as seguintes notas:

Observe que ele foi muito bem em 3 provas e resolve não fazer a última para dedicar-se a outras matérias. Sua média será 28 / 4 = 7

Essa média (7) não é o "meio" entre sua nota máxima 10 e sua nota mínima 0. Esta ideia, na verdade, corresponde ao ponto médio, que de fato é a média aritmética entre os valores máximo e mínimo de uma base de dados (ou de uma escala numérica).

Podemos continuar indagando: o que significa, dentro de uma visão aplicada, dizer que a cotação média do lote de 1000 ações da Companhia analisada, no mês de referência, foi de R$ 23,95?

Vejamos a seguir mais exemplos que poderão nos ajudar a refletir sobre esses dados.

Imaginemos agora que todos os 30 aprovados em um concurso público, para um cargo bastante concorrido, ficaram com pontuação final entre 96,35 e 99,20 pontos (numa escala de zero a cem pontos). Poder-se-ia inferir que essas notas foram suficientemente próximas (por enquanto com base unicamente no bom senso), de modo que a performance dos 30 aprovados (ou 30 primeiros classificados) foi semelhante. Caso fôssemos informados que a nota média deste grupo foi de 98,07, será que, mesmo com as ressalvas já feitas anteriormente, seríamos capazes de afirmar que ela reflete com fidelidade a performance do grupo?

3 - Dispersão dos Dados: variância, desvio-padrão e coeficiente de variação.

a) Variância e desvio-padrão

Uma primeira possibilidade, para avaliar a variabilidade ou dispersão da base de dados, seria falar na amplitude do intervalo, que apresenta os mesmos procedimentos de cálculo para dados amostrais e para dados populacionais.

No exemplo da cotação do lote de ações da Companhia C, teríamos:

Amplitude = valor máximo - valor mínimo = 27,05 - 20,32
Amplitude = 6,73

Esta análise não ajudaria muito, considerando que uma amplitude, mesmo quando considerada grande, nada indica quanto à distribuição dos dados, ou seja, diz muito pouco quanto à variabilidade deles (pode-se ter, por exemplo, uma grande amplitude com pequena variabilidade).

Pode-se então pensar em uma medida cujo ponto de partida seja a comparação de cada um dos valores da base de dados com o valor médio, buscando avaliar se a base de dados, como um todo, está suficientemente próxima da média.

Evidentemente, eventuais pontos discrepantes - aqueles pontos que "fogem" de um perfil, quer seja ele homogêneo ou heterogêneo, valores excessivamente grandes ou excessivamente pequenos, quando comparados com os demais - não são representados adequadamente pelo valor médio.

Chega-se então a uma medida denominada variância, que é calculada, para dados amostrais, da seguinte maneira:

Se os dados a serem analisados forem populacionais, isto é, todos os dados existentes, a variância (σ ²) será dada por:

Perceba que, na formulação utilizada para a determinação da variância populacional, o denominador da expressão é dado apenas por "n", que indica o número de dados em análise. Já para uma base de dados amostrais, esse denominador será "n-1". Essa subtração de uma unidade no denominador da variância amostral está ligada à redução de um grau de liberdade (GL) que passamos a ter quando trabalhamos com esses dados.

Devemos lembrar que, na análise de dados amostrais, estamos, na verdade, tentando caracterizar informações de sua população de origem e a redução de uma unidade no denominador da expressão da variância faz com que, matematicamente, este valor fique um pouco maior, tentando garantir a explicação da dispersão total dos dados populacionais que deram origem à amostra que está sendo estudada.

Então, apenas para reforçar o conceito:

No exemplo das ações, como estamos trabalhando com apenas algumas ações então estamos trabalhando apenas com uma amostra, logo deveremos utilizar a fórmula dos dados amostrais (n-1). Caso a fizéssemos uma análise com todas as ações, então deveríamos utilizar as fórmulas populacionais, ok?

Outro exemplo: suponha que você queira avaliar a média de altura dos alunos da sua sala. Caso você meça todos os alunos da sala e use esses dados para medir a média, então estará usando dados populacionais. Caso você não tenha tempo, ou não tenha como medir a altura de todos os alunos e meça apenas uma parte dos alunos, então estará trabalhando com dados amostrais. Fácil, não é?

Mais uma vez, admitindo a possibilidade de repetição de alguns dos valores, pode-se reescrever a expressão da variância amostral, por exemplo, como:

Se os dados forem populacionais, teremos:

Vamos desenvolver o cálculo para o exemplo das ações (dados amostrais) e tentar interpretar o resultado:

Variância Amostral S² = 4,11

Estamos vendo que, se tivermos muitos dados, teremos um cálculo bem grande pela frente. Entretanto se tivermos dados repetidos, podemos simplificar a fórmula incluindo um termo fi, que é na verdade a quantidade de vezes que o valor Vi se repete. Pode-se, então, reescrever a expressão da variância amostral, como:

Se os dados forem populacionais, teremos:

Vejamos um exemplo. Querendo saber qual é o gasto médio e a variância dos salários de uma pequena empresa. Os cargos, a quantidade de empregados em cada cargo e o salário de cada cargo são mostrados na tabela a seguir:

Como estamos analisando os salários, então os valores de salário são os nossos Vi, e como a quantidade é a número de funcionários com aquele salário, então esse será o nosso fi.

Vamos primeiramente calcular a média, usando a fórmula da média que leva em conta os valores repetidos:

Assim:

= (100x600)+10x10000)+(5x20000)+(1x30000) = 2500
100+10+5+1

Como estamos considerando todos os funcionários da empresa, então estamos trabalhando com dados populacionais. Logo, a variância será dada por:

σ ²= (600-2500)² x100+(10000-2500)² x10+(20000-2500)² x5+(30000-2500)² x1)
                                                       116

σ ²= (-1900)² x100+(7500)² x10+(17500)² x5+(27500)² x1)
                                            116

σ ²= 3610000x100+56250000x10+306250000x5+756250000x1 = 9675517,241
                                            116

Entendendo melhor a variância e a sua fórmula

Para entender se o grupo varia pouco ou muito temos que definir um valor de referência e verificar qual a "distância" entre cada ponto (valor de Vi) e essa referência. Qual a nossa referência? Acertou! A média!

Legal, então se soubermos a distância entre cada ponto e a média, temos uma ideia da variação do conjunto de dados? Não, você terá ideia da variação de cada ponto do conjunto, mas não uma medida de variação do conjunto, como um todo. Para ter a ideia de variação do conjunto, somamos cada uma dessas distâncias e dividimos pela quantidade de dados:

Variância do conjunto (σ²) = soma da distância de cada ponto (Vi) em relação à média / quant. de dados reescrevendo:

σ ²= Σ distância de cada ponto Vi
       quantidade de dados

Não está parecida com a fórmula original? E olha que conclusão interessante: a variação do grupo é a média das "distâncias"! Vale a pena refletir sobre isso.

Para entender o que nós estamos falando, observe a nossa fórmula da variância populacional:

Podemos ver que (V_i - µ)² representa justamente a distância de que estávamos falando: a distância entre o ponto Vi e a média.

As diferenças positivas (valores reais maiores que a média) e as diferenças negativas (valores reais menores que a média) simplesmente se anulam, o que em nada irá contribuir para que cheguemos a uma conclusão sobre a variabilidade. Elevar ao quadrado é um recurso matemático, que é utilizado para trabalhar apenas com números não negativos.

Veja um exemplo.

Desvio-padrão

Vimos que foi necessário elevar as diferenças ao quadrado para resolver um problema, entretanto, geramos outro, que é o fato da variância ter uma unidade diferente daquela unidade original dos dados. A operação inversa, raiz quadrada, deve solucionar estes dois pontos simultaneamente. Veja a seguir.

Para dados amostrais:

E para dados populacionais:

Esta nova medida é denominada desvio-padrão, simbolizada por S no caso de dados amostrais e por σ no caso de dados populacionais.

Aplicando às ações (dados amostrais), teremos:

Coeficiente de variação

Agora que já temos uma medida de variação que tem a mesma unidade dos dados originais, o desvio-padrão, já podemos responder as perguntas abaixo:

1. um desvio-padrão de R$ 2,03 significa que os dados das 22 cotações formam um conjunto suficientemente homogêneo ou não?

2. A média é capaz de retratar com fidelidade esta base de dados ou não?

3. Resumindo: o desvio-padrão de R$ 2,03, aqui encontrado, é pequeno ou grande?

Num primeiro momento a única resposta que parece adequada é:

... o desvio-padro 2,03 só pode ser considerado pequeno ou grande quando comparado com a ordem de grandeza dos dados que estão sendo analisados, pois se pouco mais de dois reais dão uma ideia de muito pouco dinheiro, isto não parece ser verdade se os preços/valores alvo de investigação são de algum dispositivo eletrônico que oscilam de 80 centavos a 3 reais e vinte centavos.

Então devemos ter uma ideia relativa deste desvio-padrão, o que dá origem a uma nova medida denominada coeficiente de variação (simbolizada por CV apresenta a mesma formulação matemática tanto para dados amostrais, como para dados populacionais):

Logo, para dados amostrais, teremos:

Já, para dados populacionais, teremos:

No exemplo, tem-se que:

Uma vantagem adicional do coeficiente de variação é a possibilidade de comparação da variabilidade de duas variáveis com unidades de medidas distintas.

Veja um Exemplo:

Um último ponto a indagar com relação à medida de variação dos dados é o seguinte:

• Qual o percentual de variação que caracterizaria um grupo como homogêneo ou heterogêneo?

Do visto até agora, percebe-se que um coeficiente de variação igual a zero ocorrerá quando todos os valores forem iguais (assim a variância é zero, o desvio-padrão é zero e, consequentemente, o coeficiente é zero por cento).

Logo, quanto mais próximo disso, maior a homogeneidade do grupo e mais consistente é a validade da média como medida representativa daqueles dados (lembrando que a média, nesse caso, poderia ser vista como o valor "capaz" de substituir todos os outros com fidelidade, devido à proximidade que estaria sendo mantida entre eles, a menos dos pontos discrepantes, que em breve seremos capazes de diagnosticar).

Uma regra empírica (baseada na experiência, no uso) indica que:

Deve-se ter um cuidado adicional com as seguintes circunstâncias:

• quando a base de dados for muito pequena (por exemplo, 10 ou 12 observações), pois um ou dois valores podem ser suficientes para gerar um coeficiente de variação mais alto, pois 1 valor em 10 corresponde a 10% da base de dados. Pode-se, neste caso, ser um pouco mais flexível com os limites de 15 e 30% indicados anteriormente;

• quando a análise estiver inserida num contexto de gestão ou controle de qualidade, um coeficiente de 12% pode ser considerado muito alto. Exemplos:

1. quando por exemplo se está analisando medidas do diâmetro, comprimento, espessura ou largura de um componente;
2. quando as avaliações implicarem risco à vida ou à integridade de indivíduos, pode-se ser sensivelmente mais rigoroso para admitir a homogeneidade da base de dados.

Para esses casos, existem técnicas estatísticas mais apropriadas.

Finalmente, é possível chegar a uma conclusão a respeito da validade da cotação média de R$ 23,95 para o lote de 1000 ações da Companhia C ao longo do mês estudado.

Como o coeficiente de variação foi de 8,48% e esse percentual pode ser considerado pequeno, então a cotação média é um bom indicador das cotações ao longo daquele mês, representando o grupo de cotações como um todo (mais uma vez destacando que será indispensável verificar a existência de pontos discrepantes, que, se existirem, devem merecer análise específica para serem interpretados corretamente).

b) Pontos discrepantes

Será que existem pontos discrepantes em nosso conjunto de dados?

Existe um teorema (desigualdade de Tchebycheff, ou Tchebichev, ou Chebychev segundo a grafia de alguns textos) que permite assegurar que para qualquer distribuição amostral de dados com uma determinada média e um determinado desvio-padrão:

Um critério, então, para o diagnóstico acerca da presença de pontos discrepantes é o seguinte:

...todos os pontos que estiverem fora do intervalo delimitado pela média mais ou menos três desvios será passível de ser considerado discrepante (ou, em outra terminologia, um outlier)...

No exemplo da cotação da Companhia C, teríamos estes "limites" dados por:

Assim, quaisquer cotações compreendidas entre R$ 17,86 e R$ 30,04 não seriam consideradas atípicas e aquelas cotações, no período observado, que fossem inferiores a R$ 17,86 ou superiores a R$ 30,04 seriam pontos atípicos, pontos discrepantes ou outliers.

Conclui-se, então, que na base de dados apresentada não há nenhuma cotação nesta situação. Isto reforça a representatividade da média para aquele contexto, embora, como já tenhamos registrado anteriormente, se o objetivo de sua empresa for realmente decidir a respeito de investir ou não na Companhia C há necessidade de uma análise mais aprofundada.

Mas e quando a média não ajuda? Quando isto ocorre, ou seja, quando a média não é validada como medida descritiva da base de dados, faz-se necessário tentar descrevê-la com o apoio de outras medidas, sob pena de não se ter uma compreensão correta a respeito do comportamento/da distribuição dos dados.

4 - A Moda

Uma primeira alternativa é a moda, que nada mais é do que o valor que aparece com a maior frequência (maior número de repetições). Uma base de dados pode ter um ou mais valores repetindo-se um mesmo número de vezes, ou até mesmo não ter nenhum valor com maior incidência que os demais. A análise da moda é a mesma tanto para dados amostrais, como para dados populacionais. A classificação fica:

Distribuição Bimodal
Exemplo das cotações das ações

Representação Gráfica de uma Distribuição Bimodal

Mais uma vez é necessária parcimônia quando da interpretação prática desta medida, pois ela pode induzir equívocos. No exemplo da Companhia C, qual seria a moda?

As cotações de R$ 23,14 e R$ 27,05 aparecem duas vezes, enquanto todas as demais apenas uma vez, logo temos duas modas que são estes dois valores. Dizer que a moda, por ser o valor que mais aparece, representa/descreve o grupo pode estar longe de ser verdade, como é o caso que acaba de ser mostrado, pois cada um dos valores que mais aparece representa menos de 10% da base de dados, assim o "poder" da moda como medida representativa do grupo aumenta à medida que ela corresponda a um percentual expressivo do total de dados (o mesmo valendo caso haja mais de uma moda).

5 - A Mediana

Outra alternativa a ser considerada é a que segue.

Quanto maior a base de dados, maior o número de subgrupos que pode/deve ser produzido para permitir melhor visualização da distribuição dos dados.

Uma primeira possibilidade é dividir a base (ordenada de forma crescente ou decrescente) em dois subgrupos de igual tamanho. O valor que ocupa a posição central é a mediana.

Quando o número de observações for ímpar existe uma única posição central e o valor correspondente a esta posição será a mediana.

1, 2, 3, 4, 5

Porém quando o número de observações for par não há uma única posição central, mas sim duas, e a mediana será a média dos dois valores correspondentes a estas duas posições centrais. Essa análise, de determinação da mediana, também é idêntica tanto para dados amostrais, como para dados populacionais.

1, 2, 3, 4

Este seria o caso do exemplo da Companhia C. Os dados ordenados ficariam:

20,32; 21,30; 21,74; 21,75; 21,85; 22,87; 22,89; 23,04; 23,14; 23,14; 23,42; 23,56; 23,96; 24,04; 24,60; 25,69; 25,70; 26,12; 26,78; 26,88; 27,05; 27,05

Como são vinte duas posições, as centrais são as 11ª e 12ª, "ocupadas" pelas cotações R$ 23,42 e R$ 23,56, logo a mediana será dada por:

Caso fossem 21 ou 23 dados, a posição central seria única, no primeiro caso a 11ª, e no segundo a 12ª.

Quando a base de dados não é pequena permitindo fácil visualização deste centro, pode-se utilizar o recurso abaixo para identificá-lo:

Voltando à mediana calculada, a interpretação é mais ou menos óbvia, pois o valor mediano de R$ 23,49 indica que 50% das cotações foram de até R$ 23,49 enquanto 50% das cotações ficaram de R$ 23,49 para cima. Quando a base é suficientemente homogênea, em particular se não há pontos discrepantes, a mediana pode não agregar valor à análise, pois a média já fazia um bom papel. Quando a base for muito heterogênea (especialmente se for uma base grande) só a mediana não é suficiente para clarear substancialmente nossa análise descritiva.

Assim, pode-se dividir o conjunto de observações em uma quantidade maior de subgrupos. Quando se utilizam os quartis para dividir a base de dados, são gerados quatro subgrupos de igual tamanho, o primeiro deles compreendido entre o valor mínimo e o primeiro quartil, o segundo entre o primeiro e o segundo quartil (que é a própria mediana), o terceiro entre o segundo e o terceiro quartil e o quarto (e último subgrupo) entre o terceiro quartil e o valor máximo do grupo analisado.

Por analogia com a determinação da mediana, o primeiro passo para a determinação do 1º e 3º quartis é identificar sua posição na base de dados ordenada. Caso tivéssemos 100 observações (apenas para facilitar o entendimento), o 1º quartil estaria localizado entre a 25ª e 26ª posições, enquanto o 3º quartil estaria entre a 75ª e 76ª posições. A mediana (ou 2º quartil) estaria entre a 50ª e 51ª posições.

O procedimento, neste caso, e como já visto para a mediana, também seria o cálculo das médias entre os valores que ocupassem aquelas posições. Importante frisar, mais uma vez, que os quartis são três e que são valores numéricos específicos, permitindo a divisão de uma base de dados em quatro subgrupos.

No caso de 22 dados, o primeiro quartil seria o valor correspondente à 6ª posição, e o terceiro quartil seria o valor correspondente à 17ª posição, ou seja, R$ 22,87 e R$ 25,70, respectivamente (apenas relembrando que o segundo quartil, igual a R$ 23,49, foi dado pela média aritmética entre os valores localizados na 11ª e 12ª posições).

Para bases de dados maiores podem ser necessárias quebras/divisões das bases de dados em uma quantidade maior de subgrupos, por exemplo dez ou cem, o que é feito com a ajuda dos 9 decis e dos 99 percentis, respectivamente.

Na maioria dos textos estatísticos as medidas aqui tratadas são agrupadas em:

6 - O Box Plot

J. W. Tukey, em seu texto sobre Análise Exploratória de Dados, de 1977, sugere um conjunto de cinco medidas para representar uma base de dados numéricos: os valores extremos (mínimo e máximo) e os três quartis (também denominados juntas), que seriam medidas mais robustas/resistentes, considerando que seriam pouco ou nada afetadas caso houvesse variação em uma pequena quantidade daqueles dados, o que é especialmente conveniente quando a base não for suficientemente grande (medidas estatísticas descritivas calculadas a partir de bases de dados suficientemente grandes não são significativamente influenciadas, em geral, por uma pequena parte dela, mesmo que sejam valores atípicos). Estas cinco medidas fazem-se acompanhar do total de dados analisados.

Pode-se construir, a partir delas, um desenho esquemático denominado box plot ou diagrama de caixas (disponível em alguns softwares estatísticos), ilustrado com resultados, já calculados, para as ações da Companhia C.

A utilização de uma planilha eletrônica, como Microsoft Excel, muito nos ajuda, simplificando o exercício de ter que lembrar todas as fórmulas e o "trabalho braçal" de efetuar todas as contas. Certamente ela em nada contribui em termos analíticos, pois se não formos capazes de interpretar os resultados gerados ficaremos como que "perdidos", sem sermos capazes de fornecer subsídios consistentes para o processo de tomada de decisão.

Exemplo de análise de dados estatísticos publicados na mídia.

Resumo

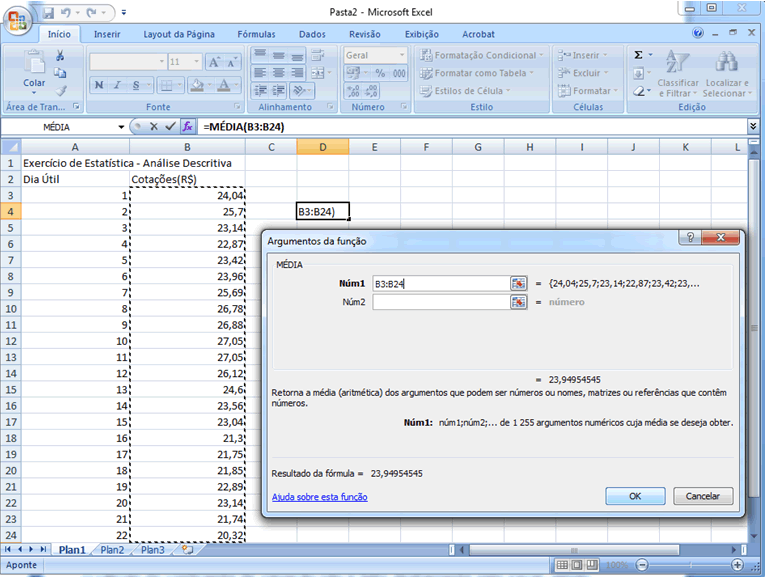
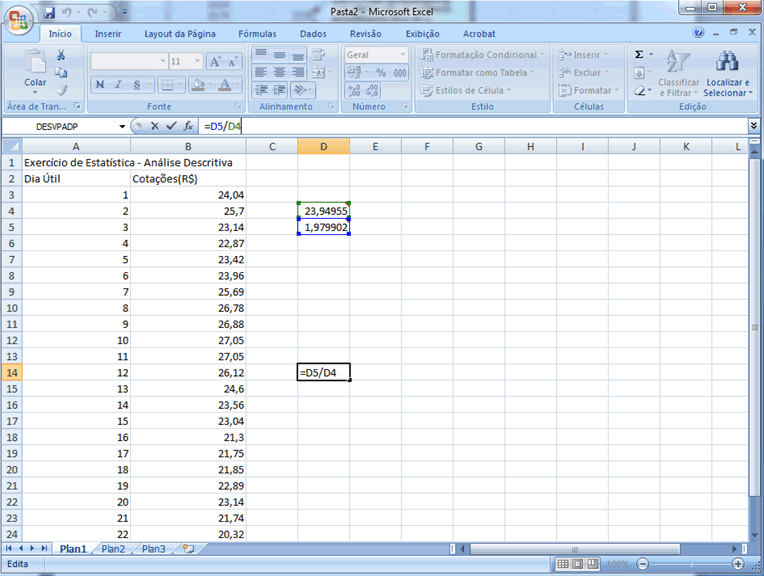
Neste módulo foram trabalhadas algumas medidas descritivas básicas para análise de uma base de dados não agrupados. Falamos da média, como medida mais simples para representar esta base, desde que a mesma seja suficientemente homogênea (ou seja, variabilidade suficientemente pequena).

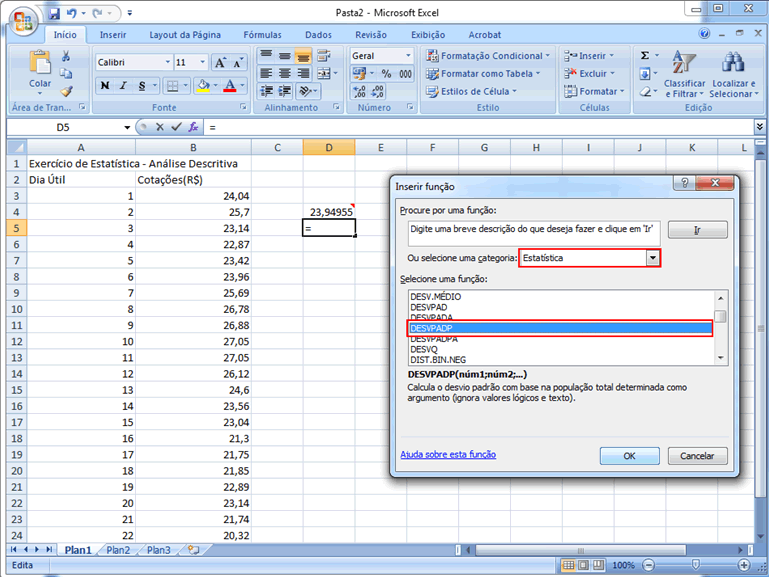
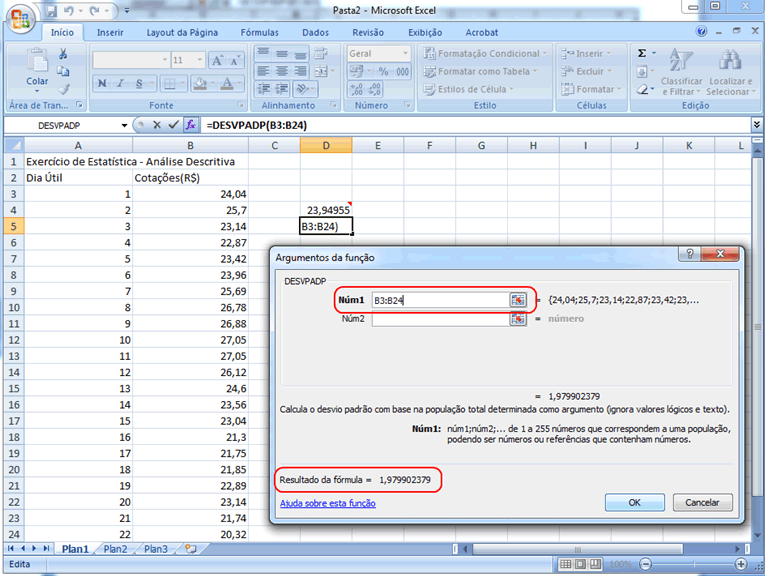
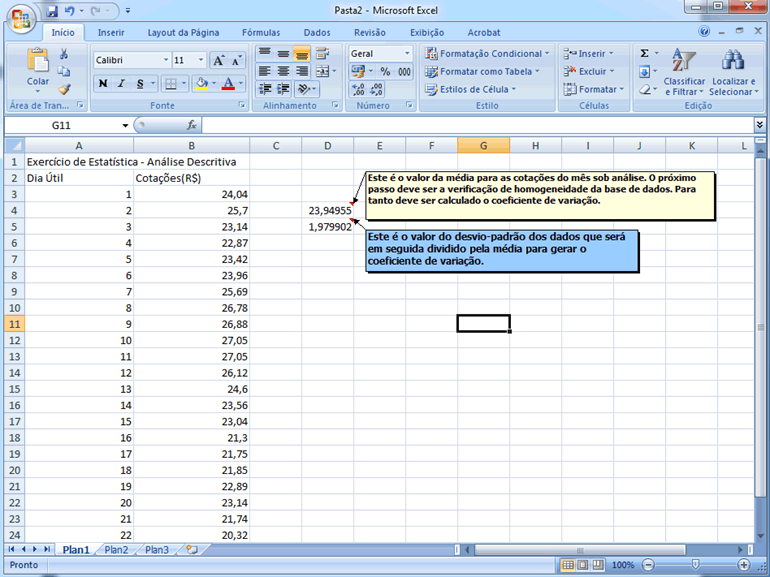
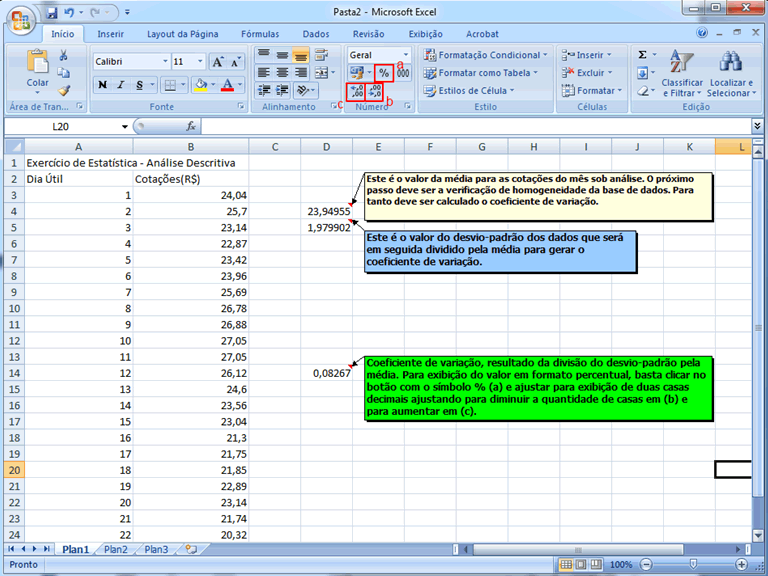
Esta avaliação da homogeneidade/heterogeneidade será feita com base no coeficiente de variação, que é uma expressão relativa do desvio-padrão (comparativamente à média), sendo então adimensional, apresentando de forma percentual a variabilidade.

Vimos que, neste caso, foram estabelecidos intervalos que, empiricamente, têm sido utilizados e aceitos como válidos para expressar a ordem de grandeza da dispersão dos dados: até 15% (pequena); acima de 15% até 30% (média) e acima de 30% (grande), devendo-se ter o cuidado de considerar o contexto sob análise, que pode exigir um limite muito inferior a 15% para admissão de homogeneidade dos dados (como muitas situações de gestão da qualidade, por exemplo).

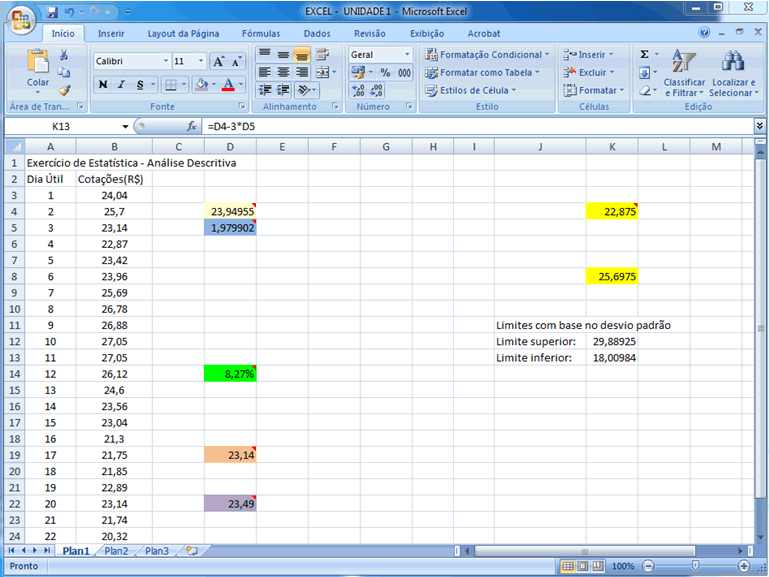
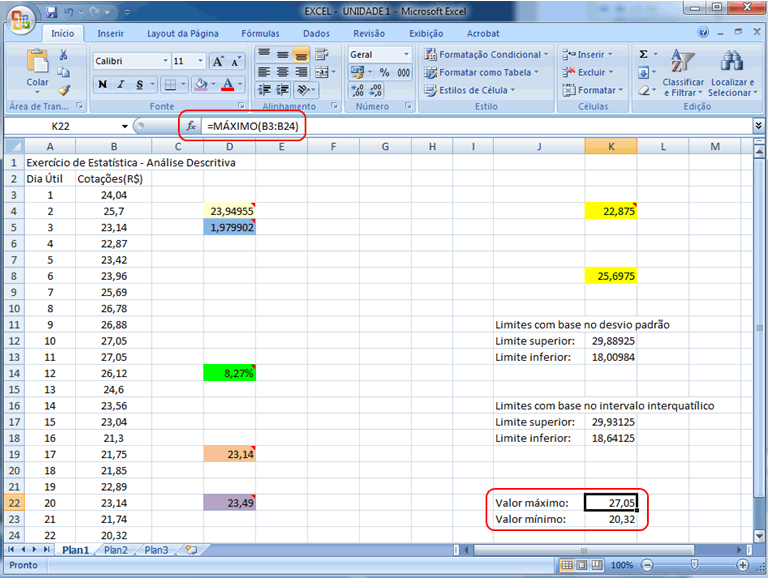
Surge então a necessidade, tanto com bases de dados homogêneas, como com heterogêneas, de diagnosticar a existência de pontos atípicos/discrepantes (ou outliers), que são aqueles que "fogem" excessivamente do perfil traçado pelo conjunto como um todo. 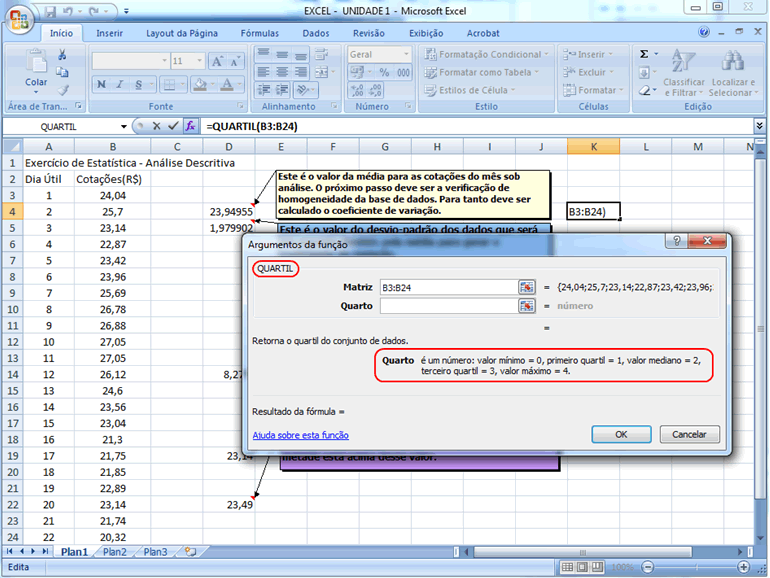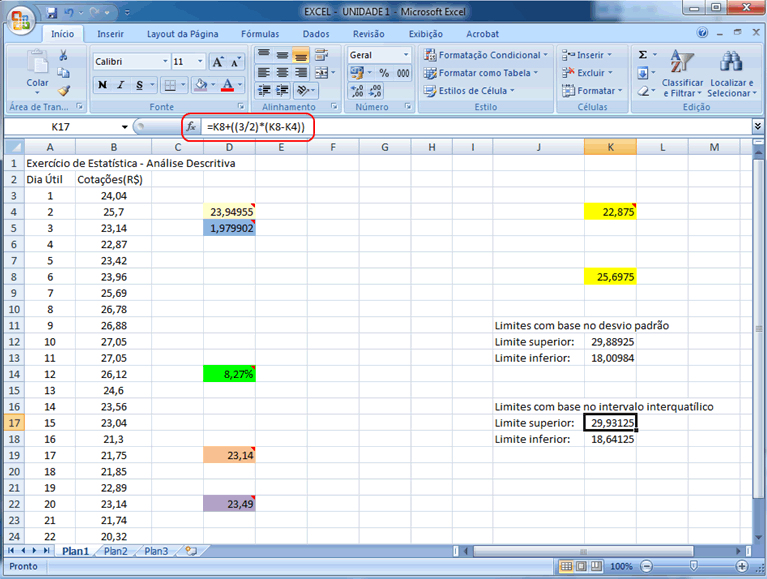Isto pode ser feito por duas abordagens: (1) estabelecer os limites máximos e mínimos de "tolerância" a partir da média mais ou menos três vezes o desvio-padrão, o que assegurará que este intervalo contenha no mínimo 88,89% dos dados amostrais (desigualdade de Tchebychev), sendo os restantes considerados pontos discrepantes; (2) estabelecer estes limites partindo do primeiro e terceiro quartis, fazendo então a diferença entre estes dois valores, multiplicando esta diferença por 3/2, somando este resultado ao terceiro quartil e subtraindo-o do primeiro quartil.

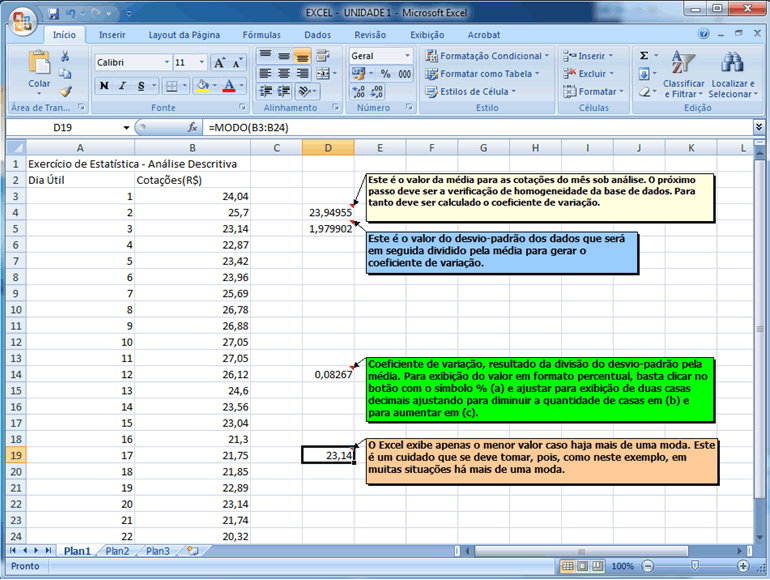
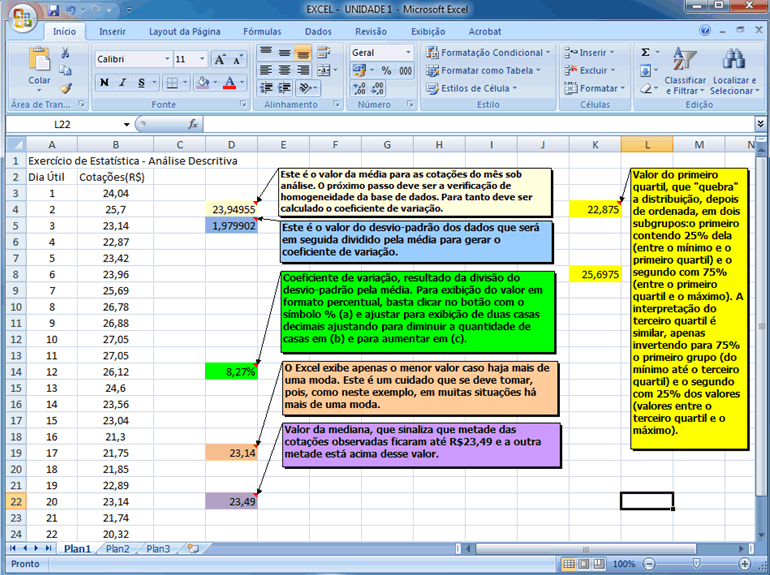
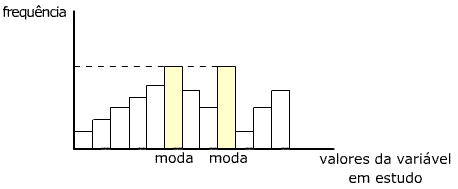
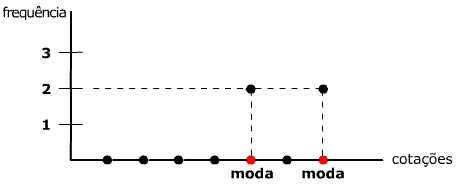
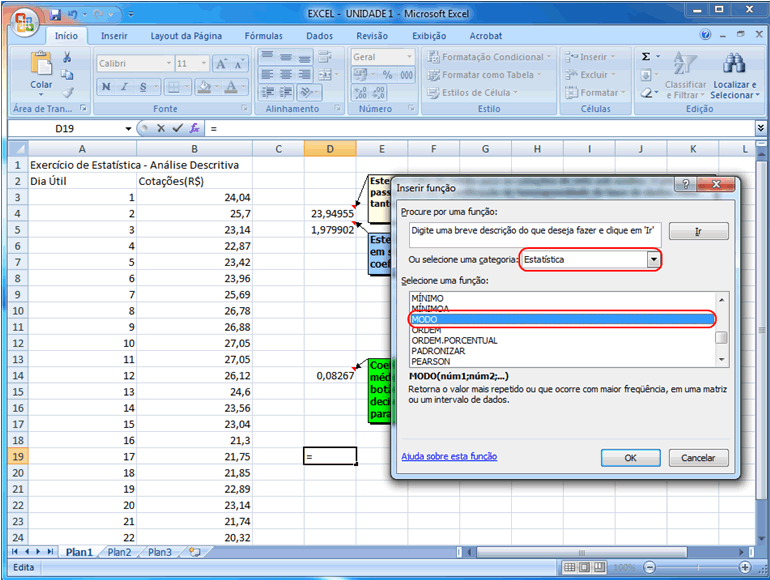
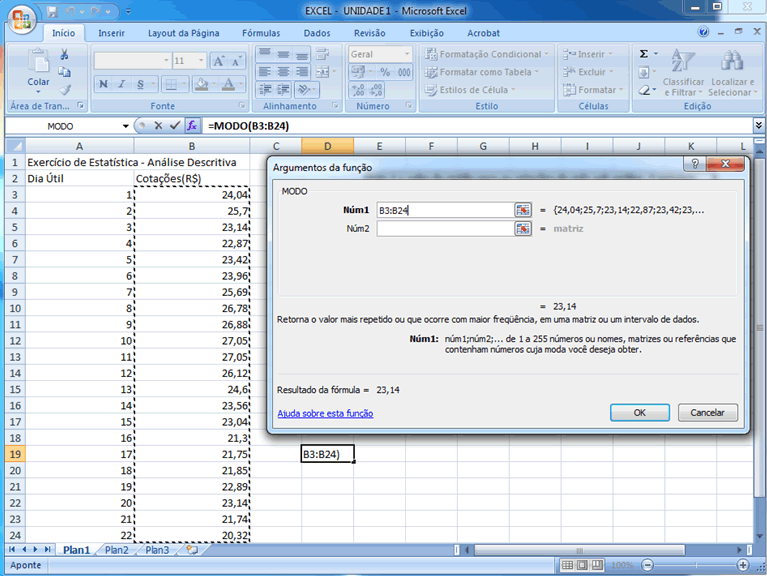
Feito isto e no caso de bases de dados que não sejam consideradas suficientemente homogêneas, deve-se partir para medidas complementares, uma vez que a média não representa o conjunto analisado, nestas circunstâncias. As medidas apresentadas foram moda, mediana e os próprios quartis (além de citação dos decis e percentis). 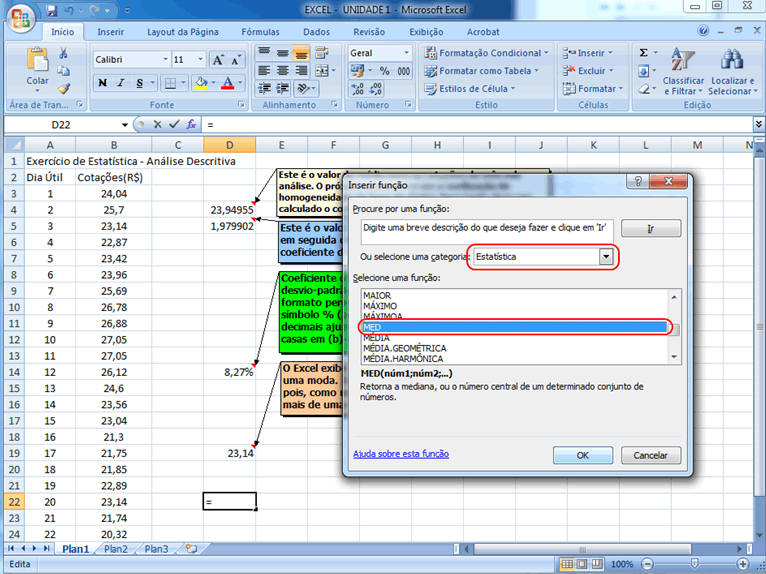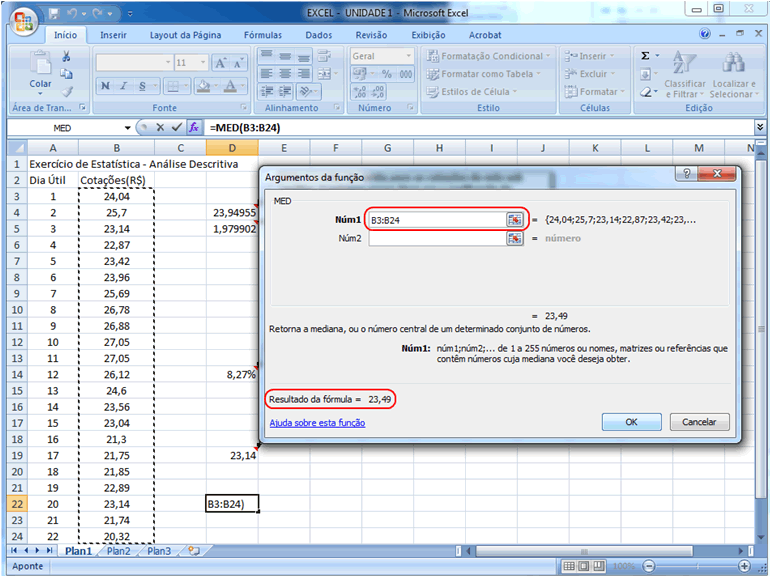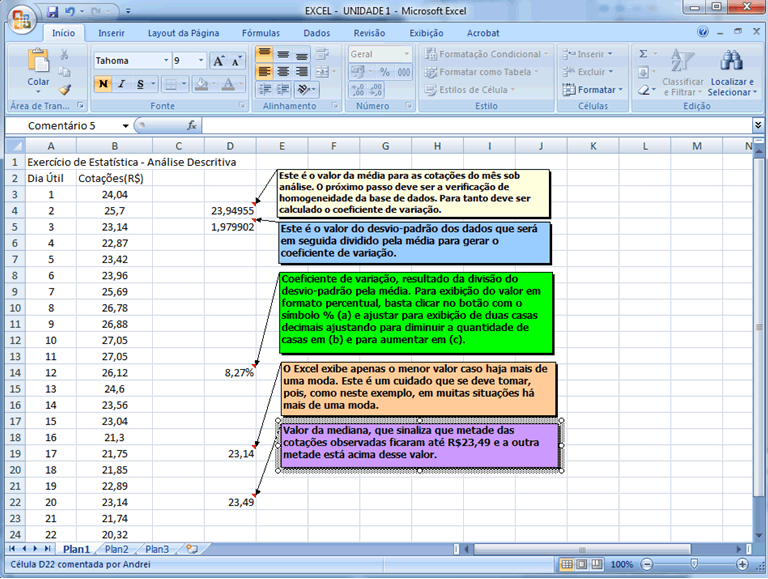A moda é o valor que mais aparece, aquele com maior incidência, o que pode agregar valor à análise desde que represente uma quantidade significativa de dados (uma moda que represente, por exemplo, dois por cento do grupo pode não caracterizar aquele valor como um destaque frente aos demais), considerando-se que a moda é única ou múltipla (ou mesmo se existe uma moda). A mediana divide o grupo, já ordenado (de forma crescente ou decrescente), deixando metade dos dados entre o valor mínimo e ela, mediana, e a outra metade entre ela e o valor máximo observado. O objetivo da utilização de valores que dividam a base de dados em grupos menores é visualizar melhor o comportamento de sua distribuição, uma vez que estes subgrupos devem ser mais homogêneos.

Foi também apresentada uma proposta sintética, idealizada por Tukey, e subsequente estrutura esquemática para suporte à análise descritiva. Apresentam-se simultaneamente os valores mínimos e máximos e os três quartis. O box-plot permite ter uma ideia a respeito da distribuição, sendo que os pontos discrepantes também são sinalizados no desenho.

1 - Determinação de Medidas Descritivas

A Planilha de Cálculo (Excel) irá nos auxiliar na tarefa de determinar o valor das medidas descritivas.

Será mantido inicialmente, até para permitir comparação, o exemplo das cotações das ações da Companhia C. O primeiro passo é abrir uma planilha e digitar os dados levantados:

2 - Calculando a Média

Após digitar os dados do exemplo da Companhia C, selecione a célula na qual você deseja que seja inserido o valor da média e posicione o cursor ali, por exemplo, célula D4, e clique no ícone f_x (colar função) da barra de ferramentas (e sinalizado na planilha abaixo):

Selecione agora as opções Estatística e Média, tal como indicado na próxima tela:

Ao clicar em OK você terá (observe que já foi feita a seleção das posições nas quais se encontram os valores, ou seja de B3 a B24, o que tanto pode ser feito com o botão esquerdo do mouse como digitando-se diretamente no campo apropriado da tela Média, iniciado por Núm1):

Já é possível ver o resultado da fórmula no canto inferior esquerdo da tela.

Ao clicar em OK o resultado da fórmula aparecerá na célula D4, originalmente selecionada, podendo-se inserir um comentário ou digitar na célula ao lado alguma nota de esclarecimento.

3 - Calculando o Coeficiente de Variação

O cálculo do coeficiente de variação não é feito diretamente pelo Excel, sendo necessário calcular o desvio-padrão para depois dividi-lo pela média. O procedimento é análogo ao cálculo da média sendo que será selecionada a célula D5 e quando da seleção da opção Estatística deve-se também selecionar DESVPADP (desvio padrão populacional). Caso você faça DESVPAD (desvio padrão amostral), o Excel adotará n-1 no denominador da variância. Assim:

Clique em OK para ir para a caixa de diálogo da função selecionada.

Em seguida, marcando as posições de B3 a B24, vem:

Mais uma vez é possível visualizar o resultado no canto inferior esquerdo da tela.

Clicando agora em OK e inserindo um comentário chega-se a:

Para que haja exibição dos comentários e não haja sobreposição, clicar em Exibir, depois em Comentários e com duplo clique na área de cada comentário é possível movê-lo de forma a permitir que todos sejam visíveis simultaneamente.

A determinação do coeficiente de variação deve ser feita dividindo-se o desvio-padrão pela média e isto será feito na célula D14 acompanhado de um comentário (como poderia ser em qualquer outra).

Deve-se lembrar que para iniciar a digitação de uma fórmula no Excel utiliza-se o sinal =, como mostrado na tela abaixo (também está sinalizado o ícone para aumento de casas decimais, mencionado no comentário):

4 - Calculando a Moda e a Mediana

Partindo agora para a determinação da moda e da mediana, a sequência inicial permanece, qual seja: selecionar uma célula na qual se deseja que a medida estatística apareça e posicionar o cursor, clicar em colar função, Estatística, MODO (no caso da moda) ou MED (no caso da mediana), OK , marcar ou digitar a posição da base de dados no campo ao lado de Num1, OK. Vejamos como fica.

Para a moda (célula D19):

Para a Mediana (célula D22):

5 - Diagnosticando Pontos Discrepantes

Falta ainda determinar os quartis e os valores limite para diagnóstico de pontos discrepantes. A determinação dos quartis é análoga, mais uma vez, a tudo que estamos fazendo. Para calcular os quartis, deve-se observar a sequência apresentada adiante.

Selecionar uma célula na qual se deseja que a medida estatística apareça e posicionar o cursor, clicar em colar função, Estatística, QUARTIL, OK, e, então surgem dois campos para preenchimento - Matriz e Quarto, como mostrado a seguir.

No campo Matriz deve-se entrar (digitando ou marcando com o mouse) com as posições de B3 a B24, como também já foi feito para as outras medidas. No caso do campo Quarto, digita-se 1, se for o primeiro quartil e digita-se 3, se for o terceiro quartil, e clica-se em OK (foram selecionadas as células K4 para inserção do valor do primeiro quartil e K8 para a do terceiro).

Consequentemente teremos:

A determinação dos limites máximo e mínimo para verificação da existência de pontos discrepantes não é feita de forma "automática" pelo Excel, sendo necessário utilizar as fórmulas já indicadas anteriormente. A seguir serão apresentadas as duas estratégias de diagnóstico de pontos discrepantes.

Primeiramente, considerando o triplo do desvio-padrão (células K12 e K13) e, em seguida, a abordagem de 3/2 do intervalo interquartílico(células K17 e K18).

Na primeira situação, depois de posicionar o cursor na célula selecionada, digitar =D4+3*D5 (para o limite máximo, observando que nas células D4 e D5 encontram-se a média e o desvio-padrão, respectivamente, e digitar =D4-3*D5 (para o limite mínimo).

No segundo procedimento, digita-se na célula selecionada para o máximo (K17), =K8+((3/2)*(K8-K4)) e na célula selecionada para o mínimo (K18), =K4-((3/2)*(K8-K4)), lembrando que em K8 está o terceiro quartil e em K4 está o primeiro quartil.

Por último utilizaremos o Excel para determinar os valores máximo e mínimo do conjunto de observações, o que é particularmente útil quando a base de dados é grande e não é possível visualizá-los com clareza. Isto é feito de forma análoga à média e desvio-padrão, devendo-se selecionar as células, posicionar o cursor, clicar em fx, Estatística, MÁXIMO ou MÍNIMO, OK, marcar ou digitar a posição da base de dados no campo ao lado de Num1 e OK. Veja na planilha abaixo os resultados nas células K22 e K23.

Resumo

Neste módulo ilustrou-se o cálculo de várias medidas descritivas apresentadas anteriormente com o apoio da planilha eletrônica Microsoft Excel. Na maioria dos casos a sequência de passos é:

(a) abrir uma planilha e digitar os dados a serem analisados;

(b) selecionar a célula na qual se quer inserir a medida e lá posicionar o cursor;

(c) clicar no ícone fx - colar função (da barra de ferramentas) e então clicar em Estatística (na coluna à esquerda, na janela que se abre);

(d) clicar em qualquer uma das opções, abaixo, na coluna à direita, na janela que está aberta:

• MÉDIA, para calcular a média;
• DESVPADP, para calcular o desvio-padrão;
• MODO, para calcular a moda;
• MED, para calcular a mediana;
• QUARTIL, para calcular os quartis (1º, 2º e 3º, sendo que o segundo é a própria mediana);
• MÁXIMO, para determinar o maior valor observado;
• MÍNIMO, para determinar o menor valor observado.

(e) clicar em OK e digitar/marcar com o mouse, na próxima janela, o conjunto de células no qual está a base de dados, no caso de cálculo de média, desvio-padrão, moda, mediana ou determinação do valor máximo e do valor mínimo. No caso de cálculo do primeiro e terceiro quartis, deve-se, depois deste passo, digitar 1 ou 3 ao lado da opção QUARTO na mesma janela (caso esta opção fosse utilizada para cálculo da mediana, bastaria digitar 2 neste campo);

(f) clicar em OK para que o resultado seja lançado na célula inicialmente selecionada.

No caso do cálculo do coeficiente de variação e dos limites para diagnóstico de pontos discrepantes, não há solução "automática" no Excel, logo, é necessário digitar as fórmulas adequadas, sempre iniciadas pelo sinal =.

É conveniente inserir comentários para cada uma das medidas calculadas, o que pode ser feito com a sequência Seleção da Célula, Inserir, Comentário, Digitação do comentário ou então com a digitação direta do comentário em célula próxima àquela na qual está o valor da medida.

1 - Distribuição Normal - Gauss

Como exemplo, podemos citar os pesos e medidas esperados para crianças recém-nascidas no primeiro ano de vida. Perceba, pelo cartão de vacinação destas crianças, que um controle destas duas variáveis é realizado, a fim de se garantir o bom desenvolvimento das crianças.

Entretanto, a lógica utilizada, através de uma função matemática, na determinação dos limites máximo e mínimo aceitáveis para os pesos e altura destas crianças, é exatamente a da determinação da distribuição normal ou de Gauss. Nessa análise leva-se em conta um peso médio e uma variação para mais ou para menos (desvio-padrão), que serve para delimitar os limites máximo e mínimo aceitáveis nas variáveis peso e altura.

Devemos lembrar que a toda função matemática corresponde um gráfico, como, por exemplo, retas, associadas às funções do primeiro grau, e parábolas, associadas às funções do segundo grau (isto para não falar nas funções exponenciais, logarítmicas e trigonométricas). Assim, esta curva normal também é fruto de uma função que pode ser expressa como:

Onde:

O aspecto gráfico, desta distribuição, de forma genérica, é o seguinte:

sendo que, no eixo horizontal, são representados os valores da variável que se está estudando e, no eixo vertical, valores associados às frequências relativas correspondentes aos valores específicos da variável sob análise.

A formulação apresentada, com certeza, apresenta uma forma bastante assustadora. Entretanto, felizmente não teremos necessidade de utilizá-la tal como se apresenta. O que a fórmula demonstra é que qualquer distribuição normal é determinada por dois parâmetros: a média e o desvio-padrão dos dados. Saiba +

Se atentássemos para as características físicas dos seres humanos, estatura, por exemplo, veríamos que a maioria dos adultos estaria na faixa que vai de 152 cm (aproximadamente) até 183 cm (aproximadamente), com muito pouca gente menor que 152 cm ou maior que 183 cm. O QI também seria previsível - a maioria dos QIs situando-se entre 90 e 110, havendo uma 'descida' gradual dos escores para ambas as caudas, com pouquíssimos 'gênios' que têm QI superior a 140 e, da mesma forma, pouquíssimas criaturas menos privilegiadas, cujos QIs estão abaixo de 60. Por igual raciocínio, relativamente poucos sujeitos poderiam ser considerados políticos extremistas - de direita ou de esquerda - enquanto a tendência política da maioria seria considerada moderada.

Finalmente, mesmo o desgaste dos pisos, resultante do fluxo de transeuntes, lembra a distribuição normal: a maior parte do desgaste ocorre no centro dos pisos (degraus etc.), enquanto nos lados, à medida que nos afastamos do centro, o desgaste vai-se tornando cada vez menor.

Observamos que o mundo hipotético da curva normal não difere de forma radical do mundo 'real' (que vivemos no momento). Fenômenos tais como estatura, QI, orientação política, desgaste dos pisos etc. aproximam-se, na prática, até que muito bem da distribuição normal teórica. Pelo fato de tantos fenômenos terem essa característica - isto é, pelo fato de ela ocorrer tão frequentemente na natureza (e por outras razões que logo se tornarão aparentes) - pesquisadores de diferentes campos têm feito uso extensivo da curva normal, aplicando-a aos dados que eles coletam e analisam.

Observe-se, porém, que alguns fenômenos no campo social - como em qualquer outro - simplesmente não se ajustam à noção teórica da distribuição normal. Muitas distribuições são assimétricas; outras têm mais de uma moda; outras são simétricas, mas não têm a forma de 'sino'.

Como exemplo concreto, consideremos a distribuição de riqueza no mundo. É fato bem conhecido que 'os que têm' superam de longe 'os que não têm'. Assim, a distribuição de riquezas (indicada pela renda per capita) é de extrema assimetria (pelo menos na aparência), de sorte que apenas uma pequena proporção da população mundial recebe porção significativa da renda total.

De forma análoga, especialistas em demografia dizem-nos que os Estados Unidos da América do Norte tornaram-se, nos últimos tempos, uma terra de jovens e velhos. Do ponto de vista econômico, essa distribuição de idades representa um fardo pesado para um grupo relativamente pequeno de trabalhadores, isto porque, sendo todos cidadãos de meia-idade, têm a seu encargo um número assustador tanto de velhos (aposentados) quanto de jovens (ainda em período escolar).

Nestas circunstâncias em que temos boas razões para esperar grandes divergências da normalidade - como, por exemplo, no caso da idade e da renda - a curva normal não pode ser usada como 'modelo' para os dados coletados. Vemos, assim, que não é possível aplicá-la com liberdade a todas as distribuições que o pesquisador obtém, e deve, ao contrário, ser usada com uma boa dose de bom senso. Felizmente os estatísticos sabem que grande quantidade de fenômenos de interesse segue o modelo normal."

Já deve ser do seu conhecimento, mesmo que apenas de ouvir falar, que vários sistemas previdenciários do mundo estão em crise ou na iminência de, se o cenário não mudar no curto e médio prazos.

2 - Padronização da Distribuição

Os fenômenos sociais, psicológicos e físicos são exemplos de fenômenos que se apresentam de forma normalmente distribuídos. Temos uma medida padrão para estas variáveis e alguma dispersão em torno desta medida. Assim, em função desta dispersão em torno da média, podemos destacar uma propriedade para este tipo de distribuição: se a base de dados estudada tem distribuição normal, pode-se garantir que:

A determinação do percentual de dados compreendidos entre determinados valores estipulados para a variável sob estudo pressupõe que haja uma padronização destes valores (vinculados à "quantidade" de desvios-padrão que cada um representa de distância relativa à média).

Sendo mais claro: considere que uma nova dieta está sendo testada em um SPA/clínica de emagrecimento. Depois de algum tempo de avaliação deste novo tratamento, observa-se que a distribuição da perda de peso (em kg) assemelha-se bastante a uma distribuição normal. Sabe-se que a perda média de peso foi de 20 kg no período estipulado para o tratamento, com desvio-padrão de 3,5 kg. Pode ser importante para a administração de algum órgão governamental de fiscalização ter uma ideia do percentual de pacientes que perderam acima de 25 kg. Tomando nossa curva, pode-se ver que:

e que o percentual desejado corresponde à área à direita do ponto 25, assinalado no eixo horizontal, lembrando que a área total da figura corresponde a 100% dos dados (ou seja = 1).

Existe um procedimento matemático formal que permite o cálculo de áreas de figuras como aquela ilustrada anteriormente, delimitada pelos valores 20 e 25. No entanto, não é uma alternativa das mais simples. De maneira alternativa, pode-se pensar em um procedimento quase "automático", aplicável a todas as situações sob análise. Isto passa pela padronização dos valores/dados que compõem a base de dados.

O que se faz é subtrair a média de todos os dados e dividir estes resultados pelo desvio-padrão, gerando-se, então, uma base de dados padronizados (também conhecidos por escores padronizados ou z).

No exemplo,

O interesse recai sobre o percentual de pessoas cuja perda de peso superou este valor padronizado de 1,43. Este procedimento para padronização dos dados viabiliza uma leitura única, independente da situação sob análise. Com isto, foi possível a construção de uma tabela da Distribuição Normal Padrão, que é apresentada na grande maioria dos livros de Estatística Básica (senão em todos).

Fundamentalmente, o que esta tabela retrata é o percentual de dados (área da figura) entre o valor padronizado e o valor médio padronizado, que sempre será zero, afinal

3 - Usando o Excel

A utilização da planilha Microsoft Excel, nos dois casos trabalhados neste módulo, também permitiria obtenção dos resultados solicitados.

No caso do primeiro exercício, é interesse o percentual de casos acima de 25 kg em uma distribuição normal cuja média é 20 kg e desvio-padrão 3,5 kg. Abrindo-se uma planilha Excel, pode-se digitar estas referências para, em seguida, utilizar a ferramenta adequada.

Posicionando o cursor na posição na qual se quer o percentual que fica abaixo do valor de referência (no caso 25 kg), clica-se no ícone fx, em seguida Estatística, em seguida DIST.NORM e OK.

Na janela aberta, há quatro campos para que sejam inseridos os valores (ou respectivas células) para geração da proporção de valores abaixo da referência a ser digitada no campo ao lado da letra X.

Observe que, no último campo, digitou-se VERDADEIRO, para obtenção da porcentagem de dados abaixo do valor de X.

Clica-se agora em OK.

O valor de 92,34% não é ainda a resposta solicitada, mas, fazendo 100% - 92,34% (ou 1 - 0,9234), chegar-se-á à solução.

O resultado obtido na planilha abaixo é praticamente o mesmo daquele obtido sem a sua utilização com uma variação quase insignificante.

No segundo exercício, será necessário usar o recurso da DIST.NORM duas vezes:

Como pode ser visto na última planilha, a seguir, o resultado foi obtido de forma análoga àquela quando foi utilizada a tabela, com geração do mesmo resultado 0,39%.

Resumo

A distribuição normal ou de Gauss é uma distribuição estatística de dados amostrais baseada na relação dos dados em análise com sua medida de tendência central (média) e com sua respectiva medida de dispersão (desvio-padrão).
Enfatizou-se a distribuição normal de dados pelo seu conjunto de características (principalmente simetria e percentuais de dados compreendidos entre a média e um, dois e três desvios-padrão para mais e para menos).

Há um conjunto de variáveis que, do ponto de vista prático, assume o aspecto de uma distribuição normal (fenômenos sociais, psicológicos e físicos), porém há um conjunto de outras que tipicamente apresentam outro formato (distribuição de renda, por exemplo).

O recurso de padronização dos dados, origina uma distribuição normal com média zero e desvio-padrão igual a um. Todas as bases de dados que formam uma distribuição normal são passíveis de serem padronizados, particularmente quando houver a necessidade de utilização de uma tabela para determinação de percentuais de dados acima de um determinado valor, abaixo de outro ou entre dois valores especificados.

Caso seja utilizada a planilha Excel, para determinação de percentuais de dados, que atendam determinadas especificações, seguir-se-á os seguintes passos:

(a) abre-se uma planilha;
(b) digitam-se os dados de média, desvio- padrão e também o valor especificado como referência;
(c) clica-se no ícone fx, em Estatística, em DIST.NORM e em OK;
(d) entra-se com o valor (ou com as respectivas células) de X (referência), com a média, com o desvio-padrão e com a palavra Verdadeiro;
(e) caso haja necessidade (no caso de ser solicitada uma porcentagem acima de um determinado valor), faz-se uma última operação complementar: 1 - o percentual obtido após a realização do passo (d).