Para entender o que nós estamos falando, observe a nossa fórmula da variância populacional:
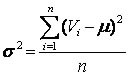
Podemos ver que (Vi - µ)² representa justamente a distância de que estávamos falando: a distância entre o ponto Vi e a média.
| Quando
todas as diferenças foram elevadas ao quadrado elas "inflacionaram"
a diferença real entre cada valor e o valor médio que
se quer validar como representativo (do ponto de vista aplicado) para
a base de dados.
Mas por que estamos trabalhando com distâncias ao quadrado? Não bastaria ter trabalhado apenas com as diferenças, sem elevá-las ao quadrado? Infelizmente não, pois as distâncias poderiam se anular, gerando um falso valor de variância, como podemos ver na imagem. |
As diferenças positivas (valores reais maiores que a média) e as diferenças negativas (valores reais menores que a média) simplesmente se anulam, o que em nada irá contribuir para que cheguemos a uma conclusão sobre a variabilidade. Elevar ao quadrado é um recurso matemático, que é utilizado para trabalhar apenas com números não negativos.
| Uma observação importante: o fato de elevar ao quadrado também faz com que a unidade de medida da variância não seja a unidade de medida original dos dados. |
Veja um exemplo.