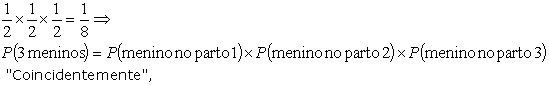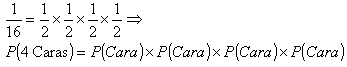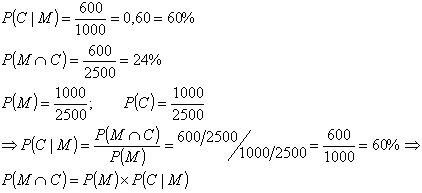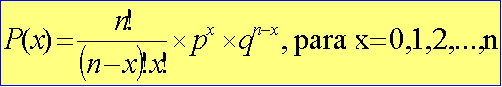1 - Conceitos iniciais

Todos nós já lidamos direta ou indiretamente com probabilidades, o que fica muito evidente para aqueles que semanalmente apostam em uma (ou mais) das loterias federais e estaduais. Também é particularmente claro para aqueles que fazem seguro de seus automóveis, residências ou seguro saúde, pois em todas essas situações está envolvida a chance de algum acontecimento (bom ou não) ocorrer.

Na história recente do nosso país, foi possível conviver com uma busca das empresas por instalação ou aluguel de geradores de energia, uma vez, que se já era desconfortável conviver com o risco de falta de energia elétrica, muito pior seria não ter um plano B para supri-la. O que não dizer, ainda, de fenômenos meteorológicos, cuja possibilidade de ocorrência tem sido antecipada e permitida chance de defesa para grandes grupos de pessoas?

Segundo a Dra. Ann van Ackere, professora associada de Ciências da Decisão na London Business School, a probabilidade e as distribuições estão no âmago da análise estatística, desde um simples jogo de cara ou coroa até sondagens de opinião pública.

Alguns termos aparecem com muita frequência quando tratamos temas para os quais a(s) probabilidade(s) deve(m) se fazer presente(s). Eles serão, então, apresentados a seguir de forma sintética e serão exemplificados.

• Espaço Amostral.
• Evento.
• Eventos mutuamente exclusivos/excludentes (ou incompatíveis).
• Eventos independentes.

2 - Possíveis Abordagens

Há três formas mais comuns de determinar probabilidades de ocorrência de eventos. São elas:

• Clássica (ou simétrica)

Requisito: eventos equiprováveis, o que significa dizer que todas as diferentes possibilidades de resultado têm exatamente a mesma chance de ocorrer.

Ex.1: dar um resultado específico no próximo sorteio da Mega-Sena ou da Dupla Sena.

Ex.2: dar um resultado específico, por exemplo, 4, quando do lançamento de um dado honesto.

Genericamente, dado um evento E para o qual se deseja conhecer a probabilidade de ocorrência e sabendo-se serem todos os eventos do espaço amostral equiprováveis, faz-se:

Assim, a chance para acertar "no chute" a opção correta em uma questão de múltipla escolha, em que haja cinco alternativas é:

Por outro lado, se você participa de um jogo no qual se lançam dois dados e calcula-se a soma dos pontos e você aposta na soma 7, para calcular sua chance de ganhar é necessário ter ideia do espaço amostral quando são lançados dois dados simultaneamente, que será apresentado no formato (resultado do dado 1; resultado do dado 2):

S = {(1; 1), (1; 2), (1; 3), (1; 4), (1; 5), (1; 6), (2; 1), (2; 2), (2; 3), (2; 4), (2; 5), (2; 6), (3; 1), (3; 2), (3; 3), (3; 4), (3; 5), (3; 6), (4; 1); (4; 2), (4; 3), (4; 4), (4; 5), (4; 6), (5; 1), (5; 2), (5; 3), (5; 4), (5; 5), (5; 6), (6; 1), (6; 2), (6; 3), (6; 4), (6; 5), (6; 6)}

Atentando para o espaço amostral, pode-se constatar que do total de 36 possibilidades, 6 delas atendem à sua aposta: (1; 6), (2; 5), (3; 4), (4; 3), (5; 2) e (6; 1). Consequentemente, sua chance de ganhar em uma aposta é 6/36 = 1/6 = 16,67%.

• Empírica (ou experimental ou frequência relativa)

Requisito: disponibilidade de dados "experimentais" ou históricos nos quais se possa constatar a ocorrência do evento, uma vez que, se a série histórica diz que tal evento nunca aconteceu, isso não é uma garantia de que ele não ocorrerá.

Ex.1: próximo voo de uma determinada companhia aérea cair.

Ex.2: determinada marca de veículo ser roubada em uma determinada cidade brasileira durante a vigência do seguro anual.

Certamente, se a abordagem para essas duas situações fosse a clássica, simplesmente ninguém mais viajaria de avião e também ninguém mais compraria automóvel, até porque não haveria mais nenhuma seguradora disposta a segurá-lo. Isso porque só há dois eventos possíveis nos dois casos. No primeiro, o avião cai ou não, e, no segundo, o veículo é roubado ou não durante a vigência do seguro. Fossem estes eventos equiprováveis, isso faria as probabilidades de sinistro iguais a 50%. Você correria esse risco em alguma daquelas situações? É evidente que esses são casos para os quais as probabilidades de um ou outro evento do espaço amostral são bem distintas.

O que costuma ser adotado, então, é o histórico de ocorrências, pois acredita-se que, em cenários que não sejam atípicos, a incidência de um passado limitado a um certo período de tempo é um bom sinalizador da chance de novas ocorrências.

Por isso, se um determinado modelo de aeronave, de uma dada empresa, teve problemas sérios em três de suas últimas 300.000 decolagens, diz-se que a chance de um problema no presente/futuro próximo é de 1 em 100.000 (claro que se novidades tecnológicas voltadas para o quesito segurança forem incorporadas ao modelo, o cenário não é mais o mesmo, logo, a incidência de eventos passados pode não ser mais um bom sinalizador de eventos futuros).

Essa abordagem requer uma atenção especial para casos como o do avião Concorde, cuja primeira queda deu-se há poucos anos. Antes desse episódio, caso fosse de interesse estimar a probabilidade de ocorrência de acidentes com esse tipo de aeronave e, inadvertidamente, fosse adotada a abordagem empírica, qual seria a conclusão (evidentemente errada)? Como o histórico não evidenciava nenhum acidente sério com o Concorde, poder-se-ia ter uma expectativa excessivamente otimista do tipo: estima-se que realmente ele não caia, pelo menos não no curto prazo.

Esse engano não levaria muito tempo para ser "desmascarado". Faz-se necessário que outra abordagem contemple esse tipo de situação, para a qual os enfoques clássico e empírico mostram-se frágeis.

• Subjetiva

Refere-se à avaliação feita por um indivíduo ou por um grupo (em geral, especializado) da chance/viabilidade de um evento.

Ex.1: duplicação do índice médio IBOVESPA (Bolsa de Valores de São Paulo) nos próximos três anos.

Ex.2: Aumento da cotação do dólar americano subir 50% nos próximos 12 meses.

Ex.3: Brasil ganhar medalha de ouro no futebol nos próximos Jogos Olímpicos.
Para qualquer uma destas três situações ilustradas, não é possível utilizar as formulações clássica e empírica, pois há um conjunto de fatores eminentemente subjetivos, de difícil ou impossível mensuração (pelo menos segundo algum critério objetivo), que certamente impacta o fenômeno sob estudo.

Caso muito conhecido é da Bolsa de Valores (e isso vale para qualquer lugar do mundo). Certamente, você há de recordar que quando há boatos sobre a performance de uma determinada companhia ou sobre a performance da economia do país, o índice da Bolsa de Valores sofre fortes oscilações (para cima ou para baixo, dependendo da natureza dos boatos), que dias depois podem retomar um padrão julgado mais "racional".

O mesmo não poderia ser dito com relação à cotação da moeda norte-americana? Se há crise no Oriente Médio, ela pode ser influenciada. Se a crise é geograficamente mais próxima, em nossa vizinha Argentina ou outro país latino-americano (México, por exemplo), como ficam os movimentos especulativos com moeda estrangeira no Brasil?

Com os eventos esportivos, a situação é similar. Caso contrário, como estimar a probabilidade de determinado clube ser eliminado de um determinado torneio de futebol antes da fase semifinal? Como estimar a chance de um grande tenista ser o campeão em um dos quatro torneios do Grand Slam em um ano de referência ou ao longo de sua carreira?

Isso para não mencionar fenômenos meteorológicos, tais como chover no dia seguinte, um determinado vulcão entrar em erupção, um determinado tornado passar por uma cidade e assim sucessivamente.

Um conceito também aceito e comum na literatura é:

onde n é o número total de vezes que se repete o experimento e n1 é o número de vezes que o resultado E1 ocorre.

Veja um exemplo.

Resumo

Neste módulo fomos apresentados aos fundamentos básicos de probabilidade. A probabilidade, de um ponto de vista simplificado e aplicado, pode ser definida como a chance de ocorrência de um evento. O conceito de evento está diretamente relacionado ao conceito de espaço amostral. O espaço amostral é definido como o conjunto de resultados possíveis de um experimento. Logo o evento é cada um dos resultados de um experimento. Obviamente, os eventos devem necessariamente pertencer ao espaço amostral. Por exemplo, se o experimento for jogar uma vez um dado normal, então o espaço amostral consiste em todos os resultados possíveis, logo espaço amostral = {1,2,3,4,5,6}. Quando o dado for jogado e digamos que tenha caído no número 4, teremos a ocorrência de um evento com o resultado 4.

Dois ou mais eventos podem ser:

• Eventos mutuamente exclusivos/excludentes (ou incompatíveis): quando a ocorrência de um evento elimina/exclui a chance de ocorrência do outro evento.
• Eventos independentes: quando a ocorrência de um evento não agrega valor a respeito da ocorrência do outro evento.

Por fim, vimos que as três formas mais comuns de determinar probabilidades de ocorrência de eventos. São elas:

Forma Clássica (ou simétrica), que presume que os eventos são equiprováveis, o que significa dizer que todas as diferentes possibilidades de resultado têm exatamente a mesma chance de ocorrer.

Forma Empírica (ou experimental ou frequência relativa), que se baseia na utilização de dados "experimentais" ou históricos nos quais se possa constatar a ocorrência do evento, uma vez que, se a série histórica diz que tal evento nunca aconteceu, isso não é uma garantia de que ele não ocorrerá.

Forma Subjetiva, que se refere à avaliação feita por um indivíduo ou por um grupo (em geral, especializado) da chance/viabilidade de um evento. Geralmente é utilizada quando não se tem conhecimento mais aprofundado do resultado a ser obtido, seja por falta de dados, seja pela complexidade do experimento.

1 - Probabilidade de Mais de um Evento

Em várias situações, o interesse recai sobre a probabilidade de um ou outro evento, e, em outras, de um e outro evento.

Exemplos simples são: qual a chance de tirar 4 ou 5 no lançamento de um dado? Qual a chance de nascimento de três meninos nos três partos previstos para a noite de hoje em uma maternidade (considerando que o sexo dos bebês não é conhecido a priori)?

Considere o quadro a seguir, resultado de um levantamento em uma grande empresa, por ocasião de um novo acordo trabalhista, a respeito da proposta de substituição de benefícios por dinheiro.

Uma vez que será formada uma comissão, com participação de um representante dos empregados, vamos calcular as probabilidades de que um empregado desse grupo selecionado ao acaso, desse grupo, seja:

• Do sexo feminino contrário à proposta;
• Indiferente;
• Ou do sexo masculino ou contrário à proposta;
• Contrário à proposta sabendo-se que é do sexo feminino.

Vamos tentar uma abordagem mais genérica desse problema, inicialmente denominando cada possível resultado como um evento, assim teríamos os seguintes eventos:

H - empregado do sexo masculino;
M - empregado do sexo feminino;
F - empregado favorável à proposta;
I - empregado indiferente à proposta;
C - empregado contrário à proposta.

As probabilidades solicitadas poderiam ser "formatadas" da seguinte maneira:

Tem-se aqui a interseção de dois eventos porque é necessário que duas condições sejam simultaneamente satisfeitas.

Tem-se aqui a união de dois eventos porque uma dentre duas situações sendo satisfeita, tem-se que a condição genérica foi satisfeita.

Inicialmente foi dito que é necessário excluir uma determinada quantidade referente a uma dupla contagem, isto é, aquelas unidades que satisfazem ambas as condições são contadas duas vezes. Satisfazer, simultaneamente, as duas condições são sinônimas de ser a interseção dos eventos, logo:

Se os eventos sob análise forem mutuamente exclusivos, a regra da adição fica reduzida à soma das probabilidades dos dois eventos. Como exemplo, considere que se joga um dado, e o que se quer é a probabilidade de sair ou um número par ou o número 5. Deve estar suficientemente claro que estes dois eventos (resultado par e resultado 5) são mutuamente exclusivos, pois 5 não é um número par, o que torna impossível a ocorrência simultânea destes eventos (assim a probabilidade de sua interseção é zero). Em decorrência:

A notação utilizada nesse item significa apenas que se quer a probabilidade do evento C, uma vez que o evento M já aconteceu, ou dado que o evento M aconteceu. Essa é uma probabilidade condicional ou probabilidade a posteriori.

Retomando um pouco a ideia explorada no item (a), ou seja, ocorrência de um evento e também de um outro evento, vamos considerar outras situações:

1 - Qual a probabilidade de nascimento de três meninos nos três nascimentos previstos para a noite de hoje em uma maternidade?

O espaço amostral fica:
S = {(menina, menina, menina); (menina, menina, menino); (menina, menino, menina); (menino, menina, menina); (menina, menino, menino); (menino, menina, menino); (menino, menino, menina); (menino, menino, menino)}
Em consequência, a probabilidade solicitada é =

Em cada parto, já é sabido que a probabilidade de nascimento de um menino é 1/2 (pelo menos sob condições "normais").

2 - Qual a probabilidade de acertar duas questões de um teste (múltipla escolha com cinco alternativas), de forma absolutamente casual (completamente no "chute"), tendo assinalado as opções b e c?

Aqui o espaço amostral é:

S = {(a, a); (a, b); (a, c); (a, d); (a, e); (b, a); (b, b); (b, c); (b, d); (b, e); (c, a); (c, b); (c, c); (c, d); (c, e); (d, a); (d, b); (d, c); (d, d); (d, e); (e, a); (e, b); (e, c); (e, d); (e, e)}

A probabilidade solicitada é:

Acertar uma questão específica, dessa natureza, no "chute", é 1/5 e, mais uma vez, "coincidentemente":

3 - Qual a probabilidade de saírem 4 caras, em quatro lançamentos de uma moeda (ou no lançamento de 4 moedas)?

Espaço Amostral = S = {(Cara, Cara, Cara, Cara); (Cara, Cara, Cara, Coroa); (Cara, Cara, Coroa, Cara); (Cara, Coroa, Cara, Cara); (Coroa, Cara, Cara, Cara); (Cara, Cara, Coroa, Coroa); (Cara, Coroa, Cara, Coroa); (Coroa, Cara, Cara, Coroa); (Cara, Coroa, Coroa, Cara); (Coroa, Cara, Coroa, Cara); (Coroa, Coroa, Cara, Cara); (Cara, Coroa, Coroa, Coroa); (Coroa, Cara, Coroa, Coroa); (Coroa, Coroa, Cara, Coroa); (Coroa, Coroa, Coroa, Cara); (Coroa, Coroa, Coroa, Coroa)}

Probabilidade questionada:

Mais uma vez, é fácil constatar que

A partir desses três exemplos, poderíamos ser levados a crer que a probabilidade de ocorrência de dois oumais eventos é dada pelo produto das probabilidades de cada um deles.

Consideremos esse "princípio" para o item (a) anterior, P(M e C):

Mas já vimos, anteriormente, que a probabilidade verdadeira é 24% e não 16%, o que nos leva a concluirque há algum problema nesse segundo procedimento.

Para concluir o desenvolvimento desse raciocínio, retomemos o resultado do item (d), no qual também foi solicitada uma probabilidade envolvendo os eventos "empregado do sexo feminino" e "empregado contrário à proposta".

O que está sendo dito é que a probabilidade da ocorrência de dois eventos é dada pelo produto da probabilidade de ocorrência de um deles, pela probabilidade de ocorrência do outro condicionado ao fato do primeiro ter ocorrido. A diferença significativa entre este caso e as três situações ilustradas é que para aquelas os eventos eram independentes, o que não ocorre aqui. Como já foi dito, dois eventos são independentes se a ocorrência de um deles não afeta a probabilidade de ocorrência do outro. Então, em havendo independência, pois saber que um evento já ocorreu não agrega nenhum valor a respeito da ocorrência do segundo.

Logo, quando essa for a situação, isto é, quando os eventos forem independentes, aí sim,

O que foi discutido, tanto para o caso de um e outros eventos, como para o caso de um e outro eventos, pode ser estendido para mais de dois, evidentemente com as adequações que se fizerem necessárias. Por exemplo, se o interesse recaísse sobre a probabilidade de ocorrência de um evento A ou de um evento B ou de um evento C, a formulação adequada ficaria:

Será deixado a critério de sua curiosidade tentar chegar a essa expressão, o que certamente não será tão difícil se o princípio estabelecido foi bem compreendido.

Para finalizar essa seção, serão apresentados: a) Teorema de Bayes; b) uma situação bastante ilustrativa, citada em Mario Triola (1999).

a) O teorema de Thomas Bayes (1702-1761) estabeleceu que as probabilidades devem ser revistas quando conhecemos algo mais sobre os eventos. Isso deve, na verdade, ser entendido como uma generalização da probabilidade condicional.

A formulação apropriada estabelece que:

que é a probabilidade de ocorrência do evento Ci, supondo-se a ocorrência do evento A, podendo-se pensar em C1, ..., Cn como um conjunto de hipóteses, sendo somente uma delas verdadeira. Dado que A já ocorreu, a probabilidade "original" de Ci ocorrer (probabilidade a priori) sofre uma alteração para P(Ci|A), que é obtida a partir da formulação acima (probabilidade a posteriori).

Um exemplo apresentado por Bussab e Morettin deve ajudar consideravelmente no entendimento correto dessa abordagem:

“Para selecionar seus funcionários, uma empresa oferece aos candidatos um curso de treinamento durante uma semana. No final do curso, eles são submetidos a uma prova e 25% são classificados como bons (B), 50% como médios (M) e os restantes 25% como fracos (F). Para facilitar a seleção, a empresa pretende substituir o treinamento por um teste contendo questões referentes aos conhecimentos gerais e específicos. Para isto, gostaria de conhecer qual a probabilidade de um indivíduo aprovado no teste ser considerado fraco, caso fizesse o curso. Assim, neste ano, antes do início do curso, os candidatos foram submetidos ao teste e receberam o conceito aprovado (A) ou reprovado (B). No final do curso, obtiveram-se as seguintes probabilidades condicionais:

P(A|B) = 0,80, P(A|M) = 0,50, P(A|F) = 0,20

Queremos encontrar P(F|A) e, pelo teorema de Bayes, essa probabilidade é dada por

Então, apenas 10% dos aprovados seriam classificados como fracos durante o curso. De modo análogo, podemos encontrar P(B|A) = 0,40 e P(M|A)=0,50, que poderiam fornecer subsídios para ajudar na decisão de substituir o treinamento pelo teste.”

b) Exemplo do Mario Triola (1999)

“Motores a Jato Independentes.

Um jato de três motores decolou do Aeroporto Internacional de Miami com destino à América do Sul, mas um dos motores falhou logo após a decolagem. Enquanto o avião retornava à pista, os outros dois motores também falharam, mas o piloto conseguiu fazer uma aterrissagem segura. Com três motores independentes, a probabilidade de todos os três falharem simultaneamente é de apenas 0,00013, ou seja, uma chance em um trilhão. As autoridades do Ministério da Aeronáutica americano constataram que um mesmo mecânico havia trocado o óleo nas três turbinas, colocando incorretamente os anéis de vedação da entrada de óleo. A utilização de três motores distintos independentes tem por objetivo aumentar a segurança, mas a interferência de um único mecânico tornou os motores dependentes. Os processos de manutenção exigem agora que os motores sejam vistoriados e ajustados por mecânicos diferentes.”

2 - Valor Esperado

Um valor esperado é simplesmente uma média dos possíveis resultados ponderados por suas respectivas probabilidades de ocorrência, assim, para uma variável X discreta:

As aplicações do valor esperado, também denominado de expectância ou esperança matemática, são diversificadas e desempenham papel de significativa importância quando se trabalha com teoria da decisão.

O valor esperado não assume, necessariamente, um dos possíveis valores da distribuição, como, por exemplo, a pontuação esperada do lançamento de um dado honesto é 3,5 (tendo em vista os possíveis resultados de 1 a 6 e as probabilidades iguais a 1/6 para cada um deles). Em outro caso poder-se-ia obter o número esperado de crianças em uma família igual a 2,4.

Veremos, a seguir, um exemplo proposto por Smailes e McGrane, em seu texto Estatística Aplicada à Administração com Excel.

"Um pequeno estabelecimento de hospedagem que oferece somente café da manhã possui dois quartos duplos idênticos. Diariamente, o lucro depende da ocupação, sendo que se faz $5 de lucro com um hóspede, $10 com dois hóspedes, $22 com três hóspedes e $45 com quatro hóspedes. As probabilidades de os números de hóspedes solicitando quartos a cada noite são:

P(1 hóspede) = 0,15
P(2 hóspedes) = 0,45
P(3 hóspedes) = 0,30
P(4 hóspedes) = 0,10

Encontre o valor esperado do lucro diário.

Se x = lucro de um quarto ocupado é →
E(x) = ($5 x 0,15) + ($10 x 0,45) + ($22 x 0,30) + ($45 x 0,10) = $16,35

O lucro diário médio do estabelecimento será de $18,60.

Observe que o lucro diário real não será de $18,60. Essa é a quantidade média que será feita por dia no decorrer de um longo período."

Resumo

Há duas regras clássicas e bastante úteis quando se trabalha com probabilidades de mais de um evento:

1. Regra da adição, em contextos para os quais se quer probabilidade de ocorrência de um evento ou de outro(s)

2. Regra do produto, em contextos para os quais se quer a probabilidade de ocorrência tanto de um como de outro(s) evento(s)

Surge, então, a necessidade de um tratamento mais formal para as probabilidades condicionais, ou a posteriori, e o Teorema de Bayes cumpre papel de destaque, sendo sua formulação:

A noção de valor esperado inclui uma "associação" entre os diferentes resultados possíveis, ponderados por suas respectivas probabilidades, a fim de gerar um resultado esperado "médio" sob certas circunstâncias.

1 - Contextualizando uma situação prática

Admita que uma nova e "revolucionária" escola secundária esteja para ser inaugurada em sua cidade e a área de compras esteja prestes a encomendar as carteiras, que devem ser adaptadas para estudantes canhotos. Dispondo-se de um dado, de fonte bastante confiável, de que 10% da população na faixa etária de 14 a 20 anos é constituída de canhotos, e sabendo-se ainda que uma turma terá quinze alunos, qual a probabilidade de que se tenha exatamente três canhotos em uma determinada sala?

Essa situação pode ser abordada da seguinte forma:

P(ser canhoto) = 0,10 → P(ser destro) = 0,90

Considerando que um grupo de 15 alunos esteja arbitrariamente de 1 a 15, a probabilidade de que exatamente os alunos de números 1, 2 e 3 fossem canhotos, admite, implicitamente, que os de números 4 a 15 não sejam. Como os eventos ser canhoto ou não são independentes (isso parece bastante lógico, salvo se considerarmos alguns casos particulares, como por exemplo irmãos em uma mesma sala), podemos pensar em:

P(alunos 1,2 e 3 canhotos) = P(aluno 1 canhoto) x P(aluno 2 canhoto) x P(aluno 3 canhoto) x P(aluno 4 destro) x P(aluno 5 destro) x P(aluno 6 destro) x P(aluno 7 destro) x P(aluno 8 destro) x P(aluno 9 destro) x P(aluno 10 destro) x P(aluno 11 destro) x P(aluno 12 destro) x P(aluno 13 destro) x P(aluno 14 destro) x P(aluno 15 destro) =
= P(aluno canhoto)³ x P(aluno destro)¹²=
= 0,10³ x 0,90¹²

Porém deve-se também considerar que outro trio qualquer pode ser de canhotos e não apenas os alunos 1, 2 e 3. Assim, há um conjunto bem maior de diferentes possibilidades para 3 alunos canhotos em um grupo de 15. Como foi tratado no caso da Mega-Sena, esse é um caso típico de combinação de 3 elementos tomados em 15, cujo resultado é dado por:

15! / [(15 - 3)! x 3!] = 15! / [12! x 3!] = 15 x 14 x 13 / 3! = 455

Finalmente, sabemos que há 455 diferentes trios de canhotos possíveis em um grupo de 15 alunos, cada um deles com probabilidade, nesse caso, de 0,103 x 0,9012. Como os 455 resultados são mutuamente exclusivos, o resultado dessa probabilidade fica:

P(3 canhotos) = 455 x 0,10³ x 0,90¹² = 0,129 = 12,9%

O caso das carteiras para canhotos reflete a situação conhecida como experimento binomial cujos pré-requisitos a serem satisfeitos são:

• número fixo de provas;
• provas independentes;
• cada prova com apenas duas possibilidades de resultado;
• probabilidades não variam de uma prova para outra.

Generalizando o resultado do exemplo, chegar-se-ia a:

Onde:
n = número de provas (ou repetições)
x = número de sucessos (ocorrências de interesse) nas n provas
p = probabilidade de sucesso em qualquer prova
q = probabilidade de insucesso (ocorrência alternativa à de interesse) em qualquer prova (sendo q = 1 - p).

Reescrevendo:

Você talvez se lembre de que o símbolo da exclamação denota o fatorial de um número, que é um produto de fatores decrescentes, assim 3! = 3 x 2 x 1 = 6.

Caso fosse indagada a probabilidade de até 3 alunos (no máximo 3) canhotos, teríamos que fazer:

P(nenhum canhoto) + P(um canhoto) + P(dois canhotos) + P(três canhotos) =

0,90¹⁵ + (15 x 0,10 x 0,90¹⁴) + (105 x 0,10² x 0,90¹³) + (455 x 0,10³ x 0,90¹²)
= 0,9444 = 94,44%

Esse último resultado implica que a chance de mais de 3 alunos canhotos em uma mesma turma com 15 alunos é de 100% - 94,44% = 5,56%.

O tratamento dado anteriormente à distribuição normal é totalmente passível de tratamento eminentemente probabilístico. A opção pela forma de abordagem, tal como foi feita, visou unicamente simplificar e prepará-lo para o que aqui foi discutido, uma vez que a ideia de chance, quantidade de pessoas/elementos com determinadas características foi contemplada naquela oportunidade.

Resumo

A distribuição binomial é aplicável às situações para as quais haja apenas duas alternativas de resposta em cada uma das diferentes repetições/tentativas independentes que se deva considerar.

As probabilidades associadas aos dois possíveis resultados não podem se alterar nas diferentes repetições. Nesse contexto, quando se quer a probabilidade de um determinado número k de ocorrências (sucessos), em n repetições/tentativas, faz-se:

1 - Distribuição Binomial no Excel

Vamos utilizar a planilha Excel para resolver as duas situações abordadas na distribuição binomial, ou seja, chance de 3 canhotos em um grupo de 15 (com probabilidade de 10% de canhotos na população) e chance de até 3 canhotos (inclusive).

Abrindo-se uma planilha Excel, pode-se digitar os valores-chave para resolução do problema ou partir direto para a função apropriada. Aqui adotaremos a primeira alternativa, por acreditarmos que ficará mais claro:

Agora, com o cursor na célula B5 (onde se quer que o resultado apareça), clica-se em fx, Estatística, DISTRBINOM e OK, o que faz surgir a janela:

No campo Núm_s, entra-se com a célula B2, onde está o número de canhotos-referência para a questão (caso se tivesse optado por entrar direto na função da distribuição binomial, agora dever-se-ia digitar o número 3 nesse campo).

No campo Tentativas, entra-se com a célula B3, onde está o número de alunos previsto para cada turma (caso se tivesse optado por entrar direto na função da distribuição binomial, agora dever-se-ia digitar o número 15 nesse campo).

No campo Probabilidade_s, entra-se com a célula B4, onde está a probabilidade associada ao evento ser canhoto (caso se tivesse optado por entrar direto na função da distribuição binomial, agora dever-se-ia digitar o número 0,1 nesse campo).

No campo Cumulativo, digita-se FALSO, pois aqui foi perguntada a probabilidade de exatamente 3 canhotos no grupo.

Já é possível ver o resultado de 12,85% (0.128505439) na própria janela de diálogo, que, por aproximação, anteriormente havia sido calculada em 12,9%.

Clica-se OK e parte-se para o cálculo da probabilidade de até 3 canhotos, para a qual será utilizada a célula B6 e procedimento análogo ao seguido até agora. A única diferença é que no campo Cumulativo deve-se digitar VERDADEIRO, uma vez que se quer a probabilidade de todas as possibilidades de 0 até 3 canhotos somadas. A resposta é 94,44%, que aparecerá na célula B6 assim que se clicar OK.

Assim:

Resumo

A distribuição binomial é aplicável às situações para as quais haja apenas duas alternativas de resposta em cada uma das diferentes repetições/tentativas independentes que se deva considerar.

As probabilidades associadas aos dois possíveis resultados não podem se alterar nas diferentes repetições. Nesse contexto, a utilização da planilha Excel em muito simplifica os cálculos de probabilidade, bastando abrir uma planilha e clicar a sequência fx, Estatística, DISTRIBINOM, OK, entrar com os valores ou respectivas células nos campos Núm_s, Tentativas, Probabilidad_s, Cumulativo (nesse caso VERDADEIRO ou FALSO), clicar novamente em OK.