Unidade 1 Módulo 1
Tela 1
Módulo I - Revisão de Matemática
1 - Razão

Podemos definir razão como o quociente entre dois valores de mesma grandeza, denominados: antecedente e conseqüente.
Matematicamente:

Exemplo:

Suponha que dos cem funcionários de uma empresa, 70 sejam homens e 30 sejam mulheres. Com base nesta informação, podemos calcular, por exemplo:

a) A razão entre homens e mulheres que trabalham na empresa:

O que indica que, para cada sete homens, a empresa possui três mulheres no seu quadro de funcionários.

b) A razão entre mulheres e homens que trabalham na empresa:

O que indica que, para cada três mulheres, a empresa possui sete homens no seu quadro de funcionários.

c) A razão entre homens e o total de funcionários da empresa:

O que indica que sete, em cada dez funcionários que a empresa possui, são do sexo masculino.

Tela 2
Módulo I - Revisão de Matemática
2 - Proporção

Uma proporção pode ser definida como a igualdade entre duas razões onde, conforme definido em sua propriedade fundamental, o produto dos meios é igual ao produto dos extremos.

Exemplo:

Propriedade Fundamental 100 x 7 = 70 x 10

Observação: Diz-se que 70 está para 100, assim como 7 está para 10.

Tela 3
Módulo I - Revisão de Matemática
3 - Regra de Três Simples

É a constituição de uma proporção mediante a comparação de duas razões.

Exemplo:

Se 5 Kg de banana custam R$ 10,00, qual o preço de 20 Kg?

Solução:

Considerando que o preço é proporcional ao peso em quilogramas, podemos dizer que 5Kg está para 20Kg, assim como R$10,00 está para “X”, ou seja:

Com base na propriedade fundamental da proporção, onde o produto dos meios é igual ao produto dos extremos:

20 x 10,00 = 5 x X

200 = 5X

X = 200/5

X = 40,00

Resposta: 20Kg de banana custarão R$ 40,00

Tela 4
Módulo I - Revisão de Matemática
4 - Potenciação

É a multiplicação de um número, por ele mesmo, quantas vezes estiverem indicadas em seu expoente.

Genericamente:

Onde:
a = base (valor que será multiplicado)
n = expoente (número de vezes em que deverá ser multiplicada a base)

Regras:
  • Todo número elevado à unidade será igual a ele mesmo.

  • Todo número elevado a zero será igual à unidade.

  • Todo número elevado a um expoente negativo será igual a uma fração na qual a unidade será o numerador e o próprio número será o denominador elevado ao expoente com sinal positivo.

  • Na multiplicação de potências de mesma base, conserva-se a base e somam-se os expoentes.

  • Na divisão de potências de mesma base, conserva-se a base e subtraem-se os expoentes.

  • Na multiplicação de potências de bases diferentes, porém com o mesmo expoente, multiplicam-se as bases e conserva-se os expoentes.


  • Outras regras:

Tela 5
Módulo I - Revisão de Matemática
5 - Radiciação


É a operação inversa da potenciação. Muito importante para resolvermos problemas com potências de expoente fracionário!


A equação acima revela que toda potência de expoente fracionário pode ser representada por uma raiz, e vice-versa, onde:

  • A base da potência (a) será o radicando da raiz;
  • O numerador do expoente (m) será o expoente do radicando
  • O denominador do expoente (n) será o índice do radical

Exemplo: calcule o valor de quatro elevado a 0,5.

Tela 6
Módulo I - Revisão de Matemática
6 - Logaritmos

Dados dois números “a” e “N”, com a1, denomina-se logaritmo de “N” na base “a” o expoente “x” ao qual se deve elevar a base “a” para obter-se o número “N”.

Matematicamente:

Observações:

a) Assume-se que a base é igual a 10 quando esta não for definida na equação;

b) Logaritmo na base “e” = “ln”, também denominado logaritmo natural ou neperiano, tem como base “e” 2,72.

Exemplos:

Tela 7
Módulo I - Revisão de Matemática
7 - Propriedades dos Logaritmos


a) Multiplicação

b) Divisão

c) Potência


Esta regra é muito importante e será utilizada sempre quando a variável desejada for o expoente. Em termos descritivos, ela nos diz que: o logaritmo de uma potência de base (a) e expoente (n) é igual ao expoente (n) multiplicado pelo logaritmo da base (a).

Exercícios Resolvidos

Tela 8
Módulo I - Revisão de Matemática
1) Encontre o valor de “i” na expressão:


Tela 9
Módulo I - Revisão de Matemática
2) Calcule o valor de “n” na equação:


Tela 10
Módulo I - Revisão de Matemática

Resumo

Neste módulo abordamos alguns conceitos de matemática básica que serão fundamentais para o desenvolvimento de nossa disciplina e que deverão servir como fonte de consulta inicial para eventuais dúvidas no decorrer do curso.

Além de relembrarmos definições de razão, proporção, regra de três, potenciação, radiciação e logaritmo, relacionamos algumas propriedades afetas a estes assuntos e necessárias ao bom entendimento dos procedimentos de cálculo que envolve a matemática financeira.

Dentre os conceitos abordados neste módulo, os principais foram:


Razão: quociente entre dois valores de mesma grandeza, denominados: antecedente e conseqüente.

Proporção: pode ser definida como a igualdade entre duas razões onde, conforme definido em sua propriedade fundamental, o produto dos meios é igual ao produto dos extremos.

Regra de Três Simples: é a constituição de uma proporção mediante a comparação de duas razões.

Potenciação: consiste na multiplicação de um número, por ele mesmo, quantas vezes estiverem indicadas em seu expoente.

Radiciação: operação inversa da potenciação é utilizada para a solução de potências de expoente fracionário.

Logaritmos: denomina-se logaritmo de “N” na base “a” o expoente “x” ao qual deve-se elevar a base “a” para obter-se o número “N”.


Unidade 1 Módulo 2
Tela 11
Módulo II - Conceitos Básicos e Regime de Capitalização Simples
1 - Introdução

O estudo da matemática financeira é de fundamental importância, em nível pessoal, para orientar decisões de poupança e de consumo, ou profissionalmente, auxiliando decisões de financiamento e investimento na empresa. Baseia-se em fundamentos básicos da matemática, aplicados em diversos momentos no processo de interação entre os agentes econômicos e o mercado financeiro.

O principal objetivo da matemática financeira é o estudo do valor do dinheiro ao longo do tempo, partindo-se do princípio de que o valor de determinada quantia em dinheiro sofre alterações, na medida em que o tempo passa.

Essa constatação, que muitas vezes pode passar despercebida, é facilmente compreendida se refletirmos, por exemplo, no quanto podíamos comprar com R$ 100,00 a um ano atrás e quanto podemos comprar, com o mesmo montante, nos dias atuais.

É importante salientarmos que o valor do dinheiro não se refere à quantia expressa na nota de R$ 100,00 aludida no exemplo que, evidentemente, não sofre alterações, mas no poder de compra, ou seja, na capacidade de transformação desses recursos em bens e serviços.

Para desenvolver melhor esse conceito, vamos supor que uma pessoa tivesse a opção de receber R$ 1.000,00 hoje ou R$ 1.000,00 daqui a um ano. Não é muito imaginarmos que, agindo de forma racional, essa pessoa preferisse receber esses recursos hoje, ao invés de postergar o recebimento para daqui a um ano, afinal, não seria esta sua escolha?

Tela 12
Módulo II - Conceitos Básicos e Regime de Capitalização Simples

Analisando melhor, veremos que se trata da opção mais racional a seguir e que pode ser justificada por um conjunto de preceitos muitas vezes intuitivos.

Mesmo considerando que a pessoa do exemplo não esteja necessitando dos recursos agora, para suprir alguma necessidade urgente, sua decisão de preferir os R$ 1.000,00 hoje pode ser justificada pelos seguintes motivos:


a. Incerteza quanto ao futuro – nada pode garantir que ela esteja aqui para receber esses recursos daqui a um ano, ou que a pessoa que irá fazer o pagamento ainda possa ou queira fazê-lo ao final deste prazo, o que implica dizer que adiar o recebimento resultará no risco de não receber os R$ 1.000,00 ao final de um ano, sem nenhuma vantagem que justifique este risco, dado que o valor permanecerá o mesmo;


b. perda do poder de compra – embora, a princípio, não necessite dos recursos neste momento para suprir alguma necessidade básica, partindo-se do princípio econômico que afirma serem os recursos disponíveis limitados e as necessidades ilimitadas, essa pessoa poderia fazer uso desse dinheiro hoje para satisfazer alguma necessidade de consumo, mesmo que supérflua. Caso adiasse o recebimento, o preço do produto ou serviço que ela seria capaz de adquirir hoje, poderia ser maior daqui a um ano, o que resultaria em perda do seu poder aquisitivo;


c. além disso, existe a hipótese de receber os recursos imediatamente e aplicá-lo em uma opção de poupança, o que evidentemente faria com que obtivesse, ao final de um ano, um valor maior do que os R$ 1.000,00.

Tela 13
Módulo II - Conceitos Básicos e Regime de Capitalização Simples

Por essas razões, é justificável supor que a pessoa irá preferir o recebimento dos R$ 1.000,00 hoje, ao invés de recebê-lo daqui a um ano. Mas, e se a pergunta fosse alterada para receber R$ 1.000,00 hoje ou R$ 1.200,00 daqui a um ano?

Ao contrário da primeira questão, temos agora dois montantes distintos ocorrendo em datas diferentes, o que insere certa complexidade no problema e exige algum tipo de instrumento que nos facilite a decisão.

Nesse sentido, como veremos mais adiante, a matemática financeira pode nos auxiliar no processo de decisão, na medida em que transforme os montantes em questão em valores efetivamente comparáveis.

Para o momento, vamos adiar a solução do problema e nos voltarmos para certos conceitos que serão necessários para a sua solução.

Tela 14
Módulo II - Conceitos Básicos e Regime de Capitalização Simples

2 - Juros

Podemos conceituar juros sob dois enfoques, partindo-se do princípio de que sua ocorrência se dará sempre com o envolvimento de dois tipos de agentes econômicos:


O agente deficitário ou devedor – pessoa que toma os recursos emprestados, a fim de satisfazer alguma necessidade e o

Credor ou agente superavitário – aquele que dispõe de sobras de recursos e empresta-os aos agentes deficitários.

Sob o enfoque do devedor – os juros podem ser vistos como o preço do fator de capital, ou a remuneração devida pela utilização do capital durante o período de tempo do empréstimo.

Na visão do credor – os juros representam um prêmio por não consumir, ou seja, pela decisão de adiar para uma data futura o consumo que poderia ser realizado hoje.

Em termos econômicos, os juros cumprem um papel importante, na medida em que servem como estímulo à poupança que, por sua vez, constitui-se em um dos alicerces para a geração de investimentos produtivos e para o crescimento da economia.

Tela 15
Módulo II - Conceitos Básicos e Regime de Capitalização Simples

Para que tudo isso ocorra, no entanto, faz-se necessário que a taxa de juros seja suficiente para:

Com relação aos três itens acima, podemos dizer que todos eles trazem certa subjetividade e estão relacionados às características de cada agente econômico. Assim, o valor dos juros necessários para compensar o risco, depende da percepção do agente econômico quanto ao grau desse risco e de quanto ele exige ganhar para aceitá-lo, conceito que decorre de uma visão pessoal.

As expectativas do agente quanto ao poder de compra do dinheiro servirão de parâmetro para aceitar os juros propostos. Caso a expectativa de inflação seja maior do que os juros oferecidos o agente, a princípio, não irá aceitá-lo.

O custo de oportunidade também irá depender do agente econômico, dado que as oportunidades de investimento são diferentes para cada pessoa.

Se observarmos bem, estes conceitos estão relacionados à nossa questão inicial do curso e, embora ainda sejam insuficientes, começam a nos dar uma noção de como responder a questão relacionada a receber R$ 1.000,00 hoje ou R$ 1.200,00 daqui a um ano.

Tela 16
Módulo II - Conceitos Básicos e Regime de Capitalização Simples

As taxas de juros podem ser representadas na forma percentual ou na forma unitária.

Taxa percentual – refere-se aos “centos” do capital, ou seja, ao valor dos juros para cada centésima parte dos recursos envolvidos na operação.

Exemplo:
Qual será o juro obtido por um capital de R$ 1.000,00 aplicado em uma opção de investimento que rende 20% ao ano, ao final de um ano?

Solução:

O enunciado indica que para cada R$ 100,00 aplicados se ganha R$ 20,00 (vinte por cento), assim, aplicando-se regra de três, teremos:

Taxa unitária – reflete o rendimento para cada “unidade” de capital, em certo período de tempo.

Repetindo o exemplo anterior, se para cada R$ 100 se ganha 20, para cada 1 ganha-se 0,2, ou seja, a taxa para cada unidade do capital empregado é de 0,2. Aplicando-se o conceito de regra de três, com base na taxa unitária, têm-se:

Tela 17
Módulo II - Conceitos Básicos e Regime de Capitalização Simples

Com base no exemplo, podemos verificar que, para transformarmos taxas percentuais em unitárias, basta que façamos a divisão desta taxa por cem. Caso se queira o inverso – transformar taxas unitárias em percentuais deverá multiplicar as taxas por cem, conforme demonstrado no quadro abaixo:

x 100
Taxa Percentual
Taxa Unitária
2,5%
0,025
8%
0,08
?
0,17
86%
?
1.200%
?
÷100

Resolvendo o quadro acima, transformamos a taxa unitária de 0,17 em percentual, multiplicando-a por cem e as taxas percentuais de 86% e 1.200%, dividindo-as por cem, obtendo, respectivamente, 17%, 0,86 e 12.

Observação Importante: Utilizaremos sempre a forma percentual nos enunciados do problema e para apresentar os resultados. A forma unitária será utilizada nas fórmulas para a solução dos problemas. No caso dos exercícios serem resolvidos no Excel, a taxa empregada será a percentual.

Tela 18
Módulo II - Conceitos Básicos e Regime de Capitalização Simples

3 - Fluxo de Caixa

O fluxo de caixa é um gráfico que busca representar as entradas e saídas de recursos no caixa de uma empresa ou, por exemplo, na conta corrente de uma pessoa física.

A linha horizontal do fluxo representa o tempo, onde o momento “zero” se refere à data atual e os demais períodos, 1, 2, 3 até “n”, representam os tempos (dias, meses, anos etc.) onde ocorrerão os fluxos (entradas ou saídas) de dinheiro.

Os fluxos de entradas e de saídas de recursos são representados por setas de sinal contrário. Em nosso curso, adotaremos as setas para cima para indicar as entradas e as setas para baixo para indicar as saídas de dinheiro do caixa.

Exemplo

No fluxo de caixa acima podemos verificar que no dia cinco de cada mês o senhor João da Silva têm uma entrada de recursos, decorrente de seu salário, no valor de R$ 2.000,00 e, ao longo do mês, nos dias 7, 9 e 10, desembolsos de caixa (pagamentos) de R$ 400,00, R$ 50,00 e R$ 30,00, decorrentes do pagamento de aluguel, telefone e luz, respectivamente.

O fluxo de recebimento do Sr. João da Silva é representado por uma seta apontada para cima e os fluxos de pagamento por setas apontadas para baixo.

Os pagamentos e recebimentos são distribuídos em uma linha horizontal, que representa o tempo, indicando o momento, no caso o dia, em que ocorrerá o fluxo.

Tela 19
Módulo II - Conceitos Básicos e Regime de Capitalização Simples

4 - Capitalização

Indica a metodologia e a periodicidade de cálculo dos juros empregados na operação financeira.

Quanto à periodicidade, a capitalização pode ser classificada em dois tipos básicos:

• Contínua - quando os rendimentos ocorrerem num intervalo de tempo muito reduzido ou infinitesimal. Pouco utilizada, não será objeto de nosso estudo.

Exemplo: O preço das ações no pregão da Bolsa de Valores que, dependendo da oferta e da demanda, em determinado momento, pode variar a cada segundo.

• Descontínua – objeto de nosso estudo compõe-se de dois regimes básicos:


Regime de Capitalização Simples (RCS) e
Regime de Capitalização Composto (RCC)

A característica principal deste tipo de capitalização é que os juros são calculados em intervalos mensuráveis de tempo.

Exemplo: operação de poupança, onde os juros são calculados mensalmente.

Tela 20
Módulo II - Conceitos Básicos e Regime de Capitalização Simples

No RCS o valor dos juros periódicos é calculado tendo como base o capital inicial.

Exemplo:

Digamos que uma pessoa tenha efetuado uma aplicação de R$ 1.000,00, pelo prazo de três meses, à taxa de juros simples de 2,00% ao mês.

Na tabela abaixo, podemos verificar os juros gerados pela operação, o saldo que a pessoa teria ao final de cada período e a variação deste saldo, no regime de capitalização simples:

Juros e Saldos Gerados pela Operação no RCS
Período
Capital Aplicado
Juros ao Mês
Saldo
Variação
Início mês 1
1.000,00
-
1.000,00
-
Fim mês 1
1.000,00
20,00
1.020,00
20,00
Fim mês 2
1.000,00
20,00
1.040,00
20,00
Fim mês 3
1.000,00
20,00
1.060,00
20,00

Conforme podemos notar no exemplo acima, os juros mensais são constantes e no valor de R$ 20,00. Este resultado decorre da característica do RCS, no qual a taxa de juros é aplicada sempre sobre o valor inicial da operação (0,02 x 1000).

O saldo da operação, que representa o capital inicial mais os juros gerados ao final de cada período, cresce R$ 20,00 por mês, chegando, ao final da aplicação a um valor de R$ 1.060,00.


Tela 21
Módulo II - Conceitos Básicos e Regime de Capitalização Simples

No regime de capitalização simples são empregadas as fórmulas:

1. Cálculo dos Juros

Os juros decorrentes de uma operação efetuada com base no RCS podem ser calculados mediante a aplicação da seguinte equação:

J = PV x i x n 
 (1)

Onde:

J = valor dos juros

PV = valor inicial da operação ou valor presente

i = taxa de juros (na forma unitária)

n = prazo da operação

Tela 22
Módulo II - Conceitos Básicos e Regime de Capitalização Simples

2. Cálculo do Montante

Também denominado de valor futuro (FV), representa a soma do valor inicial (PV) e dos juros da operação (J).


Por definição:

FV = PV + J            (2)

Substituindo a equação (1) na fórmula acima, tem-se:

FV = PV + PV x i x n

Ou

FV = PV x (1 + i x n)        (3)


Atenção


• A taxa de juros deve ser expressa sempre sob a forma unitária.

• O prazo da operação deve ter sua unidade (dia, mês, ano, etc.) coincidente com o período de referência da taxa de juros (diário, mensal, anual, etc.).

Tela 23
Módulo II - Conceitos Básicos e Regime de Capitalização Simples

5 - Juro Exato e Juro Comercial

Os conceitos de juros exatos e juros comerciais estão relacionados ao número de dias que será considerado para o cálculo da taxa de juros.

No juro exato utilizamos efetivamente o calendário do ano civil (365 dias) e consideramos efetivamente o número de dias de cada mês para o cálculo da taxa.

No juro comercial, admitimos para todos os meses, independente de qual seja, um prazo de 30 dias e o ano com 360 dias.

Em nosso curso iremos empregar sempre o conceito de juro comercial, dado que o mesmo facilita os cálculos, sem prejuízo ao aprendizado dos fundamentos da matemática financeira.

Exercícios Resolvidos

Tela 24
Módulo II - Conceitos Básicos e Regime de Capitalização Simples

1) Um investidor aplica R$ 2.500,00, por um prazo de cinco meses, a uma taxa de juros de 3,5% ao mês. Calcule o valor dos juros recebidos na operação.
Variáveis: Solução
PV = 2.500,00 J = PV x i x n
n = 5 meses  
i = 0,035 a.m. (taxa unitária de 3,5%) J = 2.500,00 x 0,035 x 5
J = ?  
  J = 437,50

2) Quanto terei que pagar, ao final de sete meses, se tomar emprestado uma quantia de R$ 5.000,00 a uma taxa de juros de 5% ao mês?

Variáveis: Solução
FV = ? FV = PV (1 + i x n)
n = 7 meses  
PV = 5.000,00 FV = 5.000,00 (1+ 0,05 x 7)
i = 0,05 a.m.  
  FV = 6.750,00

Tela 25
Módulo II - Conceitos Básicos e Regime de Capitalização Simples

3) Caso necessite de R$ 4.120,00 daqui a três meses, quanto deverei aplicar numa opção de poupança que paga 1% ao mês para obter este montante?

Variáveis: Solução
FV = 4.120,00 FV = PV (1 + i x n)
PV = ?  
i = 0,01 a.m. 4.120,00 = PV (1+ 0,01 x 3)
n = 3 meses PV = 4.120,00 / 1,03
  PV = 4.000,00

4) Por quantos anos um investidor deverá manter R$ 12.000,00 aplicados numa opção de investimento que paga 0,5% de juros mensais, a fim de obter R$ 14.160,00?

Variáveis: Solução
n = ? anos FV = PV (1 + i x n)
PV = 12.000,00  
i = 0,005 a.m. 14.160,00 = 12.000 (1+ 0,005 x n)
FV = 14.160,00 14.160,00 / 12.000,00 = 1 + 0,005n
  1,18 = 1 + 0,005n
  0,005n = 1,18 – 1
  n = 0,18 / 0,005
  n = 36 meses (por ser a taxa mensal)
  n = 36 / 12
  n = 3 anos
   

Tela 26
Módulo II - Conceitos Básicos e Regime de Capitalização Simples

A que taxa de juros devo aplicar certo capital, a fim de obter o dobro de seu valor, ao final de dez meses?

Variáveis: Solução
i = ? FV = PV (1 + i x n)
FV = 2 x PV  2PV = PV (1+ i x 10)
n = 10 meses 2PV / PV = 1 + 10i
J = ?   2 = 1 + 10i
  10i = 2 – 1
i = 1 / 10
i = 0,10 ao mês (taxa unitária)
ou i = 0,10 x 100
i = 10% ao mês (taxa percentual)


Observação: como o prazo é ao mês, a taxa será mensal.

Tela 27
Módulo II - Conceitos Básicos e Regime de Capitalização Simples
5) Qual será o rendimento e o montante de um capital de R$ 3.700,00 aplicado a uma taxa de juros de 12% ao ano, ao final de 4 meses?

Variáveis:

J = ?
FV = ?
PV = 3.700,00
i = 0,12 a.a.
n = 4 meses      A unidade de tempo da taxa é diferente da unidade de tempo da operação.

1º passo – transformar a taxa anual em uma taxa mensal, aplicando-se regra de três simples:
x = 0,12 x 1
      12 		= 0,01 a.m. (ou 1% a.m.) 

2º passo – após transformar a taxa poderemos, então, aplicar as fórmulas:
Rendimento (Juros) Montante
J = PV x i x n FV = PV (1+ i x n)
J = 3.700,00 x 0,01 x 4 FV = 3.700,00 (1+ 0,01 x 4)
J = 148,00 FV = 3.848,00

Tela 28
Módulo II - Conceitos Básicos e Regime de Capitalização Simples
Utilizando o Excel

1. Abra uma pasta nova que depois poderá ser arquivada com o nome de Juros Simples.

PLANILHA DE CÁLCULO PARA A FÓRMULA DOS JUROS “J”

No intervalo B2 escreva: Cálculo pela fórmula dos juros “J”.No intervalo B3:D3, digite os títulos “Variáveis”, “Dados” e “Resultado”.

No intervalo B4:B7, coloque o nome das variáveis “Juros”, “Valor Presente”, “Taxa de Juros” e “Prazo”.
Usando os recursos de formatação do Excel, formate os intervalos C4:D4 e C5:D5 como moeda (R$) e o intervalo C6:D6 como percentual %, todos com duas casas decimais.

No intervalo D4:D7 registre as fórmulas de cálculo de J, PV, i e n, utilizando a função lógica SE, ou então digite:
Na célula D4: =SE(C4="?";C5*C6*C7;"")
Na célula D5: =SE(C5="?";C4/(C6*C7);"")
Na célula D6: =SE(C6="?";C4/(C5*C7);"")
Na célula D7: =SE(C7="?";C4/(C5*C6);"")

As fórmulas acima estabelecem as relações lógicas da função. Analisando, por exemplo, a equação da célula D4, terá:


SE for cumprida a condição lógica C4 = “?”
ENTÃO calcule C5*C6*C7 e apresente o resultado na célula D4
SENÃO registre um rótulo vazio “” na célula D4
 


Caso deseje utilizar a função SE diretamente, coloque o cursor na célula D4 e selecione INSERIR, FUNÇÃO.

No campo CATEGORIA escolha: LÓGICA e no campo NOME escolha SE.

Tomando como base a equação 6.1, no campo Teste lógico insira C4=”?”; no campo Valor_se_verdadeiro, digite: C5*C6*C7 e no campo Valor_se_falso digite “” .
Ao final da digitação clique OK.
Repita os procedimentos de 8 a 11 para as células D5 a D7, com base nas equações 6.2 a 6.4.


Tela 29
Módulo II - Conceitos Básicos e Regime de Capitalização Simples

PLANILHA DE CÁLCULO PARA A FÓRMULA DO MONTANTE “FV”

1. No intervalo B9 escreva: Cálculo pela fórmula do montante “FV”.
2. No intervalo B10:D10, digite os títulos “Variáveis”, “Dados” e “Resultado”.
3. No intervalo B11:B14, coloque o nome das variáveis “Valor Presente”, “Valor Futuro”, “Taxa de Juros” e “Prazo”.
4. Usando os recursos de formatação do Excel, formate os intervalos C11:D11 e C12:D12 como moeda (R$) e o intervalo C13:D13 como percentual %, todos com duas casas decimais.
5. No intervalo D11:D14 registre as fórmulas de cálculo de PV, FV, i e n, utilizando a função lógica SE, conforme explicado nos itens de 8 a 12, ou então digite
Na célula D11: =SE(C11="?";C12/(1+C13*C14);"")
Na célula D12: =SE(C12="?";C11*(1+C13*C14);"")
Na célula D13: =SE(C13="?";(C12/C11-1)/C14;"")
Na célula D14: =SE(C14="?";(C12/C11-1)/C13;"")

Solucione os exercícios resolvidos colocando as variáveis do enunciado nos campos referentes aos “dados” e “?” no campo “dados” da variável que se deseja calcular no problema. Lembre-se de que a taxa de juros deverá ter a mesma unidade de tempo da operação e deverá ser transformada, quando necessário, mediante o uso de regra de três, antes de ser inserida na planilha.

As figuras abaixo representam as planilhas construídas mediante os procedimentos descritos:

INSERIR FIGURAS 1 E 2 - TABELA DO EXCEL CONFORME EXEMPLO

Tela 30
Módulo II - Conceitos Básicos e Regime de Capitalização Simples

Resumo

O estudo da matemática financeira tem por objetivo fornecer ao aluno um conjunto de fundamentos que o auxilie em decisões de poupança, consumo, financiamentos e investimentos, sendo de muita importância no seu dia - a - dia, tanto como pessoa física, quanto como administrador de empresas.

O objetivo principal da disciplina é o estudo do valor do dinheiro ao longo do tempo, compreendido que este valor se altera, na medida em que o tempo passa, devido a uma série de fatores, dentre eles a aplicação de juro.

Quando analisado pelo lado do devedor, o juro constitui-se no custo do capital. Pelo lado do credor, refere-se ao ganho ou prêmio pela abstenção do consumo.

A forma pela qual se calcula o juro periódico de uma operação financeira irá depender do regime de capitalização aplicado. No Regime de Capitalização Simples (RCS) o juro será calculado sempre se tendo como base o capital inicial ou valor presente da operação.

As fórmulas de cálculo para o RCS, bem como a descrição das variáveis utilizadas estão relacionadas a seguir:

(1) J = PV x i x n

(2) FV = PV (1+ i x n)

Onde:

J = valor dos juros
PV = valor inicial da operação ou valor presente
i = taxa de juros (na forma unitária)
n = prazo da operação
FV = valor futuro ou montante

Unidade 1 Módulo 3
Tela 31
Módulo III - Regime de Capitalização Composto (RCC)
1 - Introdução

Já verificamos que no Regime de Capitalização Simples (RCS) os juros são constantes e calculados mediante a aplicação da taxa sobre o capital inicial.

No RCC, o valor do juro periódico é calculado tomando-se por base não apenas o capital inicial, mas também a soma dos juros de períodos anteriores de capitalização, o que gera juros sobre juros.

Assim, ao contrário do que ocorre no RCS, onde o valor dos juros é constante para todo o período da operação, no RCC os juros são crescentes.

Como exemplo, digamos que um capital de R$ 1.000,00 seja aplicado pelo prazo de três meses, à taxa de juros compostos de 2,00% ao mês. Conforme podemos verificar na tabela abaixo, os juros gerados pela operação, o saldo ao final de cada período e a variação deste saldo são crescentes ao longo do tempo, devido ao fato de a taxa incidir não só sobre o capital inicial, mas sobre os juros de períodos anteriores.

Tabela 2 – Juros e Saldos Gerados pela Operação no RCC
Período
Capital Aplicado
Juros ao Mês
Saldo
Variação
Início mês 1
1.000,00
-
1.000,00
-
Fim mês 1
1.020,00
20,00
1.020,00
20,00
Fim mês 2
1.040,40
20,40
1.040,40
20,40
Fim mês 3
1.061,21
20,81
1.061,21
20,81

Analisando os juros da operação exemplificada acima e, tendo em vista a característica do RCC, podemos concluir:

• Dos R$ 20,40 de juros gerados no fim do segundo mês, R$ 20,00 se referem à aplicação da taxa sobre o capital (2% de 1.000) e os R$ 0,40 restantes decorrem da taxa sobre os juros ganhos no período anterior (2% de R$ 20,00);

• Da mesma forma, os R$ 20,81 de juros pagos no fim do terceiro mês correspondem a soma dos juros sobre o capital R$ 20,00 (2% de 1.000) mais os juros recebidos sobre os juros ganhos em períodos anteriores no valor de R$ 0,81 (2% de R$ 40,40).

Tendo em vista que o exemplo anterior foi o mesmo utilizado para o RCS, compare as duas tabelas e verifique as diferenças entre os dois regimes.

1. Cálculo do Montante

O valor futuro de uma operação no RCC é calculado mediante a aplicação da seguinte fórmula:

(3)

Onde:

FV = valor futuro, valor nominal ou montante

PV = valor presente, atual ou inicial

i = taxa de juros (sempre na forma unitária)

n = prazo da operação

Tela 32
Módulo III - Regime de Capitalização Composto (RCC)
2. Cálculo dos Juros

Partindo do conceito de que os juros (J) representam a diferença entre o montante (FV) e o valor inicial da operação (PV), ou seja:
(4)

Ao substituir FV da equação (3) na fórmula (4), têm-se:

  

Resolvendo a equação:

 (5)

Observações importantes:

a) A taxa de juros deve estar sempre na forma unitária.
b) O prazo da operação deve ter sua unidade (dia, mês, ano, etc.) coincidente com o período de referência da taxa de juros (diário, mensal, anual, etc.).

Tela 33
Módulo III - Regime de Capitalização Composto (RCC)

2 - Regime de Capitalização Composto – Exercícios Resolvidos:

1) Um investidor aplica R$ 2.500,00, por um prazo de cinco meses, a uma taxa de juros de 3,5% ao mês. Calcule o valor dos juros recebidos na operação.

Variáveis: Solução
PV = 2.500,00 J=PVx[(1+ i)n - 1]
n = 5 meses J=2500,00x[(1+0,035)5 - 1]
i = 0,035 a.m. (taxa unitária de 3,5%) J = 2.500,00 x 0,187686
J = ? J = 469,22

2) Quanto terei que pagar, ao final de sete meses, se tomar emprestado uma quantia de R$ 5.000,00 a uma taxa de juros de 5% ao mês?

Variáveis: Solução
FV = ? FV=PVx(1+i)n
n = 7 meses FV=5000,00x(1+0,05)7
PV = 5.000,00 FV = 5.000,00 x 1,4071
i = 0,05 a.m. FV = 7.035,50

Tela 34
Módulo III - Regime de Capitalização Composto (RCC)

3) Caso necessite de R$ 4.120,00 daqui a três meses, quanto deverei aplicar numa opção de poupança que paga 1% ao mês para obter este montante?

Variáveis: Solução
FV = 4.120,00 FV=PVx(1+i)n
n = 3 meses 4120,00=PVx(1+0,01)3
PV = ? PV = 4.120,00 / 1,030301
i = 0,01 a.m. PV = 3.998,83

Tela 35
Módulo III - Regime de Capitalização Composto (RCC)

4) Por quanto tempo um investidor deverá manter R$ 12.000,00 aplicados numa opção de investimento que paga 0,5% de juros mensais, a fim de obter R$ 14.160,00?

Variáveis: Solução
n = ? meses FV=PVx(1+i)n
PV = 12.000,00 14.160,00=12.000,00x(1+0,005)n
i = 0,005 a.m. 14.160,00 / 12.000,00 = 1,005n
FV = 14.160,00  

1,18 = 1,005n
ln 1,18 = ln1,005n
            
ln 1,18 = n x ln1,005n
n = ln 1,18 / ln 1,005
n = 0,165514 / 0,004988
n 33 meses


Tela 36
Módulo III - Regime de Capitalização Composto (RCC)
5) A que taxa de juros devo aplicar um certo capital, a fim de obter o dobro de seu valor, ao final de dez meses?

Variáveis: Solução
i = ? FV=PVx(1+i)n
FV = 2 x PV 2PV=PVx(1+i)10
n = 10 meses 2PV / PV = (1+i)10

2 = (1+i)10
=
21/10= (1+i)10/10
20,1= 1 + i
1,071773 – 1 = i
i = 0,071773
ou i = 0,071773 x 100
i 7,18% ao mês (taxa percentual)

Observação: como o prazo é ao mês, a taxa será mensal.

Tela 37
Módulo III - Regime de Capitalização Composto (RCC)

6) Qual será o rendimento e o montante de um capital de R$ 3.700,00 aplicado a uma taxa de juros de 12% ao ano, ao final de 6 meses?

Variáveis:  
J = ?
 
FV = ?  
PV = 3.700,00  
i = 0,12 a.a.  
n = 6 meses
  A unidade de tempo da taxa é diferente da unidade de tempo da operação.

1º passo – transformar o prazo mensal em uma fração anual, aplicando-se regra de três simples:

Importante: A transformação de taxas de juros compostos não pode ser efetuada mediante a aplicação de regra de três simples, mas pelo conceito de taxas equivalentes, que será visto num capítulo mais adiante. Assim, até que seja aprendido este conceito, devemos transformar o prazo da operação na unidade de tempo da taxa.

taxa   prazo (meses)
1 ano
12
 
 
x
  
6

x = 6 x 1 = 0,5 anos
........12

2º passo – após transformar a taxa poderemos, então, aplicar as fórmulas:

Rendimento (Juros) Montante
J=PVx[(1+i)n-1] FV=PVx(1+i)n
J=3.700,00x[(1+0,12)0,5-1] FV=3.700,00x(1+0,12)0,5
J = 3.700,00 x 0,058301 FV = 3.700,00 x 1,058301
J=215,71 FV=3.915,71

Tela 38
Módulo III - Regime de Capitalização Composto (RCC)

3 - Utilizando o Excel

1. Abra uma pasta nova que depois poderá ser arquivada com o nome de Juros Compostos.


PLANILHA DE CÁLCULO PARA A FÓRMULA DOS JUROS “J”

2. No intervalo B2 escreva: Cálculo pela fórmula dos juros “J”.
3. No intervalo B3:D3, digite os títulos “Variáveis”, “Dados” e “Resultado”.
4. No intervalo B4:B7, coloque o nome das variáveis “Juros”, “Valor Presente”, “Taxa de Juros” e “Prazo”.
5. Usando os recursos de formatação do Excel, formate os intervalos C4:D4 e C5:D5 como moeda (R$) e o intervalo C6:D6 como percentual %, todos com duas casas decimais.
6. No intervalo D4:D7 registre as fórmulas de cálculo de J, PV, i e n, utilizando a função lógica SE, ou então digite:

6.1 Na célula D4: =SE(C4="?";C5*((1+C6)^C7-1);"")
6.2 Na célula D5: =SE(C5="?";C4/((1+C6)^C7-1);"")
6.3 Na célula D6: =SE(C6="?";(1+(C4/C5))^(1/C7)-1;"")
6.4 Na célula D7: =SE(C7="?";LN(C4/C5+1)/LN(1+C6);"")

7. As fórmulas acima estabelecem as relações lógicas da função. Analisando, por exemplo, a equação da célula D4, terá:



SE for cumprida a condição lógica C4 = “?”
ENTÃO calcule C5*((1+C6)^C7-1) e apresente o resultado na célula D4
SENÃO registre um rótulo vazio “” na célula D4


8. Caso deseje utilizar a função SE diretamente, coloque o cursor na célula D4 e selecione INSERIR, FUNÇÃO.

9. No campo CATEGORIA escolha: LÓGICA e no campo NOME escolha SE.

10. Tomando como base a equação 6.1, no campo Teste lógico insira C4=”?”; no campo Valor_se_verdadeiro, digite: C5*((1+C6)^C7-1) e no campo Valor_se_falso digite “” .

11. Ao final da digitação clique OK.

12. Repita os procedimentos de 8 a 11 para as células D5 a D7, com base nas equações 6.2 a 6.4.

Tela 39
Módulo III - Regime de Capitalização Composto (RCC)


PLANILHA DE CÁLCULO PARA A FÓRMULA DO MONTANTE “FV”


13. No intervalo B9 escreva: Cálculo pela fórmula do montante “FV”;
14. No intervalo B10:D10, digite os títulos “Variáveis”, “Dados” e “Resultado”.
15. No intervalo B11:B14, coloque o nome das variáveis “Valor Presente”, “Valor Futuro”, “Taxa de Juros” e “Prazo”.
16. Usando os recursos de formatação do Excel, formate os intervalos C11:D11 e C12:D12 como moeda (R$) e o intervalo C13:D13 como percentual %, todos com duas casas decimais.
17. No intervalo D11:D14 utilize a função SE, conforme explicado nos passos de 9 a 11 ou registre as fórmulas de cálculo de PV, FV, i e n, conforme abaixo:

17.1 Na célula D11: =SE(C11="?";VP(C13;C14;;C12);"")
17.2 Na célula D12: =SE(C12="?";VF(C13;C14;;C11);"")
17.3 Na célula D13: =SE(C13="?";TAXA(C14;;C11;C12);"")
17.4 Na célula D14: =SE(C14="?";NPER(C13;;C11;C12);"")

18. As equações acima utilizam as funções VP, VF, Taxa e NPER do Excel.

Efetue a solução dos exercícios resolvidos no capítulo colocando as variáveis do enunciado nos campos referentes aos “dados” e “?” no campo “dados” da variável que se deseja calcular no problema. Lembre-se que a taxa de juros deverá ter a mesma unidade de tempo da operação, o que poderá exigir a transformação do prazo, mediante o uso de regra de três, antes de ser inserido na planilha.

 


IMPORTANTE! – Ao utilizar a fórmula FV do Excel os valores de PV e FV deverão ter sinais contrários. Caso PV seja inserido com valor positivo, FV deverá ser digitado com valor negativo e vice-versa, evidenciando fluxos de caixa de sentidos opostos.

As figuras abaixo representam as planilhas construídas mediante os procedimentos descritos acima:

Utilizando a HP12C

Tela 40
Módulo I - Revisão de Matemática

Utilizando a HP12C

Vamos pegar o exemplo abaixo para entendermos a resolução utilizando a calculadora financeira HP12C.

A Lepipopi Computers S.A. possui R$ 120.000 disponível em conta corrente e não deseja deixa-lo parado. O diretor financeiro explicou ao seu gerente que não precisará utilizar os recursos durante os próximos 3 meses. O seu gerente de banco, conhecendo a situação, oferece uma aplicação para este período com juros de 1%a.m. capitalizados mensalmente.

Utilizando-se a formula de juros compostos chega-se a conclusão que a empresa terá R$ 123.636,12 ao final de 3 meses.

Utilizando a fórmula estudada chegaremos ao valor da seguinte forma:
FV = PV x (1+i)n
FV = 120.000 x (1+1/100)3
FV = 120.000 X 1,0303
FV = 123.636,12

E como fazemos para resolver via HP12C ?

A HP12C é a calculadora financeira mais utilizada no mercado. No seu canto superior esquerdo, logo abaixo do visor, localizam-se as teclas utilizadas para o cálculo de juros compostos.

Tela 41
Módulo I - Revisão de Matemática

Para tanto deve-se proceder da seguinte maneira:

1º passo – Zerar a máquina

Para tanto é necessário teclar e . Este procedimento deve ser feito todas as vezes que for utilizar a máquina para evitar misturar valores que possam estar na memória da calculadora. No visor aparecerá o valor zero.

2º passo – Informar o período da 1ª capitalização

Agora, é necessário teclar e se a capitalização ou pagamento começar no mês seguinte (END) ou teclar e se a capitalização ou pagamento começar no mesmo mês (BEG). No exemplo acima a remuneração ocorrerá no mês seguinte. No visor continuará aparecendo o valor zero.

3º passo – Introduzir os dados informados
Os dados do exemplo têm seus respectivos campos na calculadora e devem ser introduzidos conforme abaixo:

• 120.000 - Armazena-se o valor no momento atual.

• 3 - Insere-se quantidade de período relativo a aplicação. No caso do exemplo, foram 3 meses.

• 1 - Insere-se a taxa do período relativo ao problema. No caso do exemplo, a taxa já foi informada em consonância com os períodos, os seja 1% a.m.

4º passo – Achar o valor que se deseja

• Teclar - A HP12C calcula o valor do montante final da aplicação de R$ 120.000 por 3 meses a uma taxa de 1%a.m.. e mostra no visor o valor de 123.636,12 que refere-se ao valor que a empresa receberá ao final de 3 meses.

Tela 42
Módulo I - Revisão de Matemática

A utilização da HP12C facilita a resolução de quaisquer problemas e não só o cálculo do Valor Futuro. Na falta de apenas um dos elementos, seja o prazo ou a taxa ou o valor presente, mas possuindo todas as outras informações, a calculadora possibilita o cálculo.

Detalhe importante. Os sinais entre o Capital Inicial (PV) e o Valor Futuro (FV) devem ser invertidos, caso contrário a calculadora produzirá a
mensagem Error 5.

A explicação é baseada na lógica de que numa situação de aplicação de recursos (poupador) ocorre o movimento de saída de recursos para a posterior entrada de fluxos e numa situação de empréstimo/financiamento (tomador de recursos) ocorre o movimento de entrada de recursos para a posterior saída de fluxos. Faça o teste, e confira se você acha as respostas abaixo.

Tela 43
Módulo III - Regime de Capitalização Composto (RCC)
Resumo

Verificamos neste capítulo que, diferentemente do que ocorre no Regime de Capitalização Simples (RCS), no qual os juros incidem sempre sobre o valor inicial, nas operações realizadas sob o Regime de Capitalização Composto (RCC) as taxas são aplicadas sobre o valor inicial mais os juros recebidos em períodos anteriores, gerando o chamado “juros sobre juros”, que se apresenta crescente durante todo o período da operação.

Dada essa característica, em problemas em que a taxa não coincidir com o prazo, até que tenhamos trabalhado a metodologia de transformação da taxa, devemos adequar o prazo, nos utilizando de regra de três simples, para poder solucionar o problema.

Em questões que envolvam a determinação do prazo e dos juros da operação, devemos fazer uso dos conceitos de logaritmo, para o prazo, e de radiciação, para taxas, ambos abordados no módulo “Revisão de Matemática”.

As fórmulas de cálculo para o RCC, bem como a descrição das variáveis utilizadas estão relacionadas a seguir:
J=PVx[(1+i)n-1]

FV=PVx(1+i)n

Onde:

J = valor dos juros
PV = valor inicial da operação ou valor presente
i = taxa de juros (na forma unitária)
n = prazo da operação
FV = valor futuro ou montante

Unidade 1 Módulo 4
Tela 44
Módulo IV - Capitalização, Descapitalização e Equivalência de Capitais
1 - Capitalização

Podemos definir capitalização como o processo que visa acrescentar juros a um determinado capital, levando-o a uma data futura.

No exemplo que serviu como base para a análise do RCC, vimos que um capital de R$ 1.000,00, aplicado a 2% ao mês, resulta num montante de R$ 1.020,00 ao final do primeiro mês, R$ 1.040,40 no segundo mês e R$ 1.061,21 ao final de três meses. Demonstrando a operação em um fluxo de caixa, têm-se:

Para encontrarmos o montante ao final de cada período aplicamos a equação FV=PVx(1+i)n onde “n” irá representar o número de períodos que acrescentaremos juros ao capital ou, sob outro ponto de vista, a data futura para qual queremos levar nosso valor presente.

A equação FV=PVx(1+i)n revela que ao multiplicarmos o valor presente (PV) por (1+i)n, encontraremos o valor futuro (FV). A expressão (1+i)n, denominada de Fator de Capitalização Composto (FCC), serve para acrescentar juros a um valor presente (PV) pelo número de períodos indicados em “n”. Assim, a partir do fluxo acima, se desejarmos saber qual o valor futuro de R$ 1.000,00 no mês “1”, basta capitalizarmos este valor por um período:


FV=PVx(1+i)n FV=1.000x(1+0,02) FV = R$1.020,00


Caso desejássemos calcular o valor dos R$ 1.000,00 no terceiro mês, consideraríamos n = 3 e, ao aplicarmos a equação acima, encontraríamos R$ 1.061,21.

Para efetuarmos a capitalização no RCS utilizamos os mesmos procedimentos do RCC, modificando apenas a fórmula. Neste caso, para o cálculo do FV aplicamos a equação FV=PV (1+i x n), onde (1+i x n) representa o fator de capitalização, ou melhor, o Fator de capitalização Simples (FCS), por estarmos utilizando o RCS no cálculo.

É importante notarmos que o valor futuro (FV) é sempre maior que o valor presente (PV), dado FV representar a soma de PV e dos juros (J).

Tela 45
Módulo IV - Capitalização, Descapitalização e Equivalência de Capitais
2 - Descapitalização

Processo inverso ao da capitalização, consiste em mover um determinado valor que ocorrerá em uma data futura, para uma data anterior à sua ocorrência.

Para efetuarmos a descapitalização, devemos retirar os juros embutidos no valor futuro (FV), a fim de determinar seu valor presente (PV), conforme demonstrado no fluxo de caixa abaixo:

Em termos matemáticos, conforme visto anteriormente, dado que:

FV = PV x (1+i)n

Se resolvermos essa equação para PV, teremos:

PV=FV x 1/(1+i)n

A equação acima revela que ao multiplicarmos o valor futuro (FV) por 1/(1+i)n encontraremos o valor presente (PV). A expressão 1/(1+i)n, denominada de Fator de Descapitalização Composto (FDC), serve para retirar os juros embutidos no valor futuro (FV) pelo número de períodos indicados em “n”. Assim, a partir do fluxo acima, se desejarmos saber qual o valor presente de R$ 1.061,21 no mês “2” , basta descapitalizarmos este valor por um período:

PV=FVx1/(1+i)n PV=1.061,21/(1+0,02) R$ 1.040,40

Caso desejássemos calcular o valor dos R$ 1.061,21 no momento zero, consideraríamos n = 3 e, ao aplicarmos a equação acima, encontraríamos R$ 1.000,00.

Para efetuarmos a descapitalização no RCS efetuamos os mesmos procedimentos utilizados para o RCC. Neste caso, o cálculo do PV é efetuado mediante o uso da equação PV = FV x 1 / (1+i x n), demonstrada no módulo anterior, onde 1 / (1+i x n) é denominado Fator de Descapitalização Simples (FDS).

Tela 46
Módulo IV - Capitalização, Descapitalização e Equivalência de Capitais
Resolvendo uma questão pendente

Quando iniciamos a abordagem dos conceitos básicos de matemática financeira, lançamos aos alunos a seguinte questão: o que você prefere receber R$ 1.000,00 hoje ou R$ 1.200,00 daqui a um ano? Lembre-se que, nesta questão, não consideramos a necessidade de recursos, mas o que seria preferível financeiramente, ou seja, o que seria mais vantajoso.

Embora tivéssemos um indicativo de que a resposta mais racional estaria relacionada à taxa de juros, não tínhamos até o momento os fundamentos necessários para a solução do problema. Agora, conhecendo os conceitos de capitalização e descapitalização, poderemos analisar o problema e chegar a uma resposta racional. Para tanto, vamos considerar que a taxa de juros oferecida pelo mercado seja igual a 30% ao ano. A partir desta taxa poderemos, então, mover os R$ 1.200,00 oferecidos para o final de um ano, utilizando-nos do conceito de descapitalização e comparar com os R$ 1.000,00 oferecidos hoje:

Como vimos anteriormente, o valor presente (PV) de um determinado valor futuro (FV) é calculado pelas seguintes equações, a depender do regime de capitalização utilizado:

RCS => PV=FV x 1/(1+i x n) => PV=1.200 x 1/(1+0,30 x 1) = 923,08
RCC => PV=FV x 1/(1+i)n => PV=1.200 x 1/(1+0,30) = 923,08

No exemplo, dado que o valor de R$ 1.200,00 ocorre daqui a apenas um período, tanto no RCS, quanto no RCC, o valor de R$ 1.200,00 (daqui a um ano) é igual a R$ 923,08 hoje.

Após a descapitalização, podemos mudar a pergunta do problema para: o que você preferiria receber hoje: R$ 923,08 (que corresponde a R$ 1.200,00 no futuro) ou R$ 1.000,00? e a resposta, neste caso, seria imediata.

Tela 47
Módulo IV - Capitalização, Descapitalização e Equivalência de Capitais

Embora tenhamos resolvido o problema mediante a descapitalização dos R$ 1.200,00, poderíamos resolvê-lo, caso quiséssemos, capitalizando os R$ 1.000,00 de hoje, para daqui a um ano, aplicando a taxa de 30%, conforme abaixo:

RCS => FV=PV x (1+i x n) => FV=1.000 x (1+0,30 x 1)=1.300,00
RCC => FV=PV(1+i)n => FV=1.000(1+0,30) = 1.300,00

Neste caso, o raciocínio seria baseado na observação de que, ao receber os R$ 1.000,00 hoje você poderia aplicá-lo e, após um ano, dada a taxa de 30% a.a., oferecida pelo mercado, retirar R$ 1.300,00, o que seria preferível, tendo em vista que a segunda opção promete somente R$ 1.200,00 ao fim deste prazo.

A partir desse problema, relativamente simples, podemos concluir que, devido ao efeito das taxas de juros ao longo do tempo, dois valores só poderão ser efetivamente comparáveis se ocorrerem numa mesma data. Então, para comparar valores que ocorrem em momentos distintos, a fim de tomar uma decisão quanto ao que seria mais vantajoso receber, devemos nos utilizar do processo de capitalização, que acrescenta juros a um determinado valor, levando-o a uma data futura, ou descapitalização, que consiste em retirar os juros embutidos em um valor futuro, trazendo-o a uma data anterior à sua ocorrência.

Colocando os valores em uma mesma data, a escolha entre os dois torna-se imediata, tendo em vista que, racionalmente, optaremos pelo menor valor, caso tenhamos que pagá-lo e pelo maior valor, no caso deste representar um recebimento.


Tela 48
Módulo IV - Capitalização, Descapitalização e Equivalência de Capitais

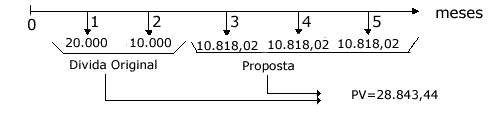
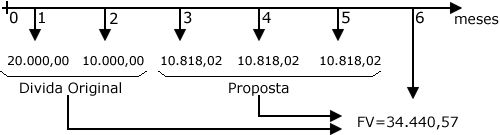
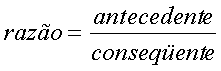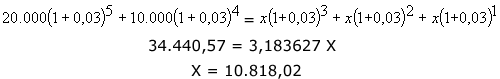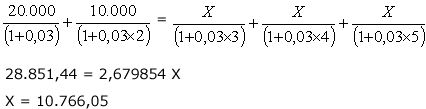Equivalência de Capitais ou Financeira

Dois ou mais capitais, representativos de certa data dizem-se equivalentes quando, a certa taxa de juros, produzem resultados iguais numa data comum.

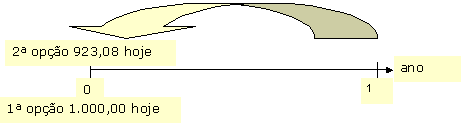
Vamos retornar à questão de receber R$ 1.000,00 hoje ou R$ 1.200,00 daqui a um ano supondo que a taxa de juros oferecida pelo mercado seja de 20% ao ano.

Utilizando-nos do processo de CAPITALIZAÇÃO, podemos obter o valor de R$ 1.000,00, que ocorre hoje, para daqui a um ano, ou, mediante o uso da DESCAPITALIZAÇÃO, calcular o valor de R$ 1.200,00, que ocorrerá somente daqui a um ano, para a data atual, aplicando os procedimentos aprendidos no início do módulo, assim:

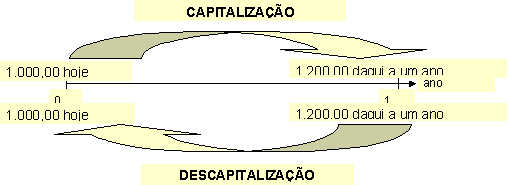
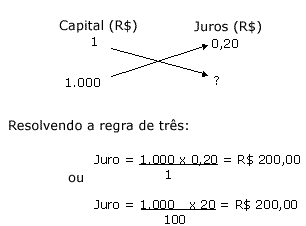
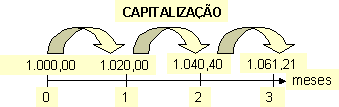
Conforme podemos verificar na figura acima, R$ 1.000,00 capitalizados por um ano, a uma taxa de 20%, correspondem a R$ 1.200,00 daqui a um ano, ou seja:

RCS => FV=PV(1+i x n) => FV=1.000 x (1+0,20 x 1) = 1.200,00
RCC => FV=PV x (1+i)n => FV=1.000 x (1+0,20)1 = 1.200,00

Da mesma forma, R$ 1.200,00 daqui a um ano, descapitalizados a 20%, são iguais a R$ 1.000,00 hoje.

RCS => PV=FVx1/(1+i x n) => PV=1.200 x 1/(1+0,20 x 1) = 1.000,00
RCC => PV=FV x 1/(1+i)n => PV=1.200 x 1/(1+0,20) = 1.000,00

Dessa maneira, podemos concluir que, a uma taxa de juros de 20% ao ano, R$ 1.000,00 hoje equivale a R$ 1.200,00 daqui a um ano, dado que, para uma mesma data, produzem resultados iguais.

Neste caso, desconsiderando qualquer outro fator que pudesse interferir na decisão de receber os recursos hoje ou daqui a um ano, ou seja, considerando apenas o valor do dinheiro no tempo e a taxa de juros do mercado, a pessoa ficaria indiferente em receber R$ 1.000,00 hoje ou R$ 1.200,00 daqui a um ano, dado que, para uma mesma data, estes valores se equivalem.


Tela 49
Módulo IV - Capitalização, Descapitalização e Equivalência de Capitais
Problemas envolvendo mais de um fluxo de caixa

Questões de equivalência de capitais que envolvem mais de um fluxo de caixa não possuem uma fórmula genérica para a solução, que depende da quantidade e periodicidade dos fluxos envolvidos no problema.

Embora essa característica, aparentemente, possa sugerir grandes dificuldades ao aluno, devemos ter em mente que todas as questões poderão ser resolvidas mediante a aplicação dos processos de capitalização e descapitalização, de acordo com cada enunciado.

Por exemplo, vamos supor que uma empresa tenha que fazer dois pagamentos a um banco, decorrentes de uma dívida contraída anteriormente, sendo: um pagamento no valor de R$ 20.000,00 para daqui a um mês e outro no valor de R$ 10.000,00 para daqui a dois meses.

Prevendo dificuldades em cumprir com sua obrigação, a empresa solicita ao banco a substituição dos pagamentos originais do contrato por três parcelas iguais e sucessivas, a primeira ocorrendo daqui a três meses.

Considerando que a taxa de juros cobrada pela instituição financeira é de 3% ao mês e, levando-se em consideração que esta taxa não será modificada no novo contrato, qual o valor das parcelas a serem pagas, em substituição ao contrato original?

Solução:

Primeiramente vamos construir o fluxo de caixa representativo do problema que, neste tipo de questão, é muito importante para visualizarmos os procedimentos de cálculo:

Dado que o problema se constitui numa substituição da dívida original pela proposta da empresa, podemos inferir que, independente do momento em que ocorrerão os fluxos de caixa, o conjunto de pagamentos da divida original deve ser equivalente ao conjunto de pagamentos da proposta, ou seja, a uma data comum, os fluxos, originais e propostos, deverão produzir o mesmo capital.

Essa conclusão nos leva a assumir que os capitais devem ser equivalentes a certa data, denominada “data focal”, que representa o momento no tempo que servirá de comparação dos valores e poderá ser, a princípio, escolhida de forma arbitrária.

Então, dando continuidade à solução do problema, vamos eleger as datas focais “0” e “6” para desenvolver a resposta, primeiramente com base no RCC.

Tela 50
Módulo IV - Capitalização, Descapitalização e Equivalência de Capitais

Resolvendo para a data focal “0” – RCC

Elegendo a data focal “0” para a solução do problema, estamos assumindo que, nesta data, o conjunto de fluxos originais será equivalente ao conjunto de fluxos da proposta, então:

Dívida Original (descapitalizada para "0") = Proposta (descapitalizada para "0")

Resolvendo a questão:

Assim, para que as três parcelas da proposta sejam equivalentes aos dois pagamentos originais elas deverão ter o valor de R$ 10.818,02 pois, trazidas à data focal zero, elas geram capitais equivalentes, no valor de R$ 28.843,44, conforme demonstrado no fluxo de caixa abaixo:

A figura acima mostra que o valor descapitalizado de qualquer um dos conjuntos de fluxos de caixa, original e proposto, são equivalentes a R$ 28.843,44, no momento “0”.

Tela 51
Módulo IV - Capitalização, Descapitalização e Equivalência de Capitais
Resolvendo para a data focal “6” – RCC

Elegendo a data focal “6” para a solução do problema, estamos assumindo que, nesta data, o conjunto de fluxos originais será equivalente ao conjunto de fluxos da proposta, então:


Dívida original (capitalizada para “6”) = Proposta (capitalizada para “6”)

Resolvendo o problema:

O resultado obtido para a data focal “6” é o mesmo encontrado para a data focal “0” e revela que os pagamentos da proposta deverão ser de R$ 10.818,02. O conjunto destes pagamentos, no momento “6”, é igual ao conjunto de pagamentos da dívida original, conforme pode ser verificado no fluxo de caixa abaixo:

A figura acima mostra que o valor capitalizado de qualquer um dos fluxos de caixa, original e proposto, são equivalentes a R$ 34.440,57, no momento “6”.

Podemos concluir, então, que independente da data focal escolhida para a solução do problema, no RCC, o resultado será sempre o mesmo.

Embora essa afirmação seja verdadeira para o RCC, conforme veremos a seguir, a mesma não se aplica para o RCS.


Tela 52
Módulo IV - Capitalização, Descapitalização e Equivalência de Capitais
Resolvendo para a data focal “0” – RCS

Baseados no mesmo raciocínio aplicado para o RCC, teremos:


Dívida original (descapitalizada para “0”) = Proposta (descapitalizada para “0”)



Tela 53
Módulo IV - Capitalização, Descapitalização e Equivalência de Capitais
Resolvendo para a data focal “6” – RCS


Dívida original (capitalizada para “6”) = Proposta (capitalizada para “6”)


20.000(1+0,03x5) + 10.000(1+0,03x4) = x(1+0,03x3) + x(1+0,03x2) + x(1+0,03)
34.200,00 = 3,18x
x=10.754,72

Com base nas respostas encontradas para o RCS, podemos verificar que, caso a data focal escolhida seja igual a “0” , as parcelas deverão ser no valor de R$ 10.766,05 e, se optarmos pela escolha da data “6”, as prestações passam para R$ 10.754,72, evidenciando que, a depender do momento escolhido como data focal, as respostas irão variar.

Este problema decorre da característica do RCS que produz juros proporcionais ao prazo da operação e que, quando fracionados, geram resultados diferentes.

Se analisarmos pelo lado do credor do exemplo, este deverá sugerir a data focal “0”, dado que as parcelas que irá receber serão maiores (R$ 10.766,05). No entanto, para o devedor, a melhor escolha será a data focal “6”, por propiciar um valor menor (R$ 10.754,72).

Dada esta característica, fica prejudicado o posicionamento da matemática financeira em problemas envolvendo equivalência de capitais a juros simples. Na prática, a solução deste tipo de questão é resolvida mediante a adoção do RCC, que fornece uma única resposta, para qualquer data focal escolhida.

Em nosso curso, iremos dar ênfase às soluções que envolvam o RCC, embora seja importante ao aluno conhecer os problemas gerados pelo RCS.

Tela 54
Módulo IV - Capitalização, Descapitalização e Equivalência de Capitais
3 - Equivalência de Capitais – Exercícios Resolvidos:

1) Uma empresa deve pagar R$ 8.500,00 daqui a três anos. Considerando uma taxa de juros de 3,5% ao ano, quanto deverá desembolsar se desejar liquidar sua dívida daqui a um ano?

Fluxo de Caixa

Solução: o valor a pagar daqui a um ano corresponde aos R$ 8.500,00 descapitalizados por dois períodos.

PV1=8.500/(1+0,035)2 = 7.934,84

Interpretação: Os R$ 7.934,84 daqui a um ano são equivalentes a R$ 8.500,00 daqui a três anos.


Importante! – podemos verificar que o conceito de valor presente não está relacionado ao valor de determinado fluxo na data de hoje (zero), mas ao valor do fluxo na data focal escolhida, qualquer que seja, desde que anterior à data prevista para o fluxo de caixa original. Como no exemplo acima, o valor presente foi encontrado no ano um (data focal) e não no momento zero.

Tela 55
Módulo IV - Capitalização, Descapitalização e Equivalência de Capitais
2) Uma empresa possui uma dívida composta de três pagamentos no valor de R$ 1.500,00, R$ 2.000,00 e R$ 2.500,00, vencíveis em 30, 60 e 90 dias, respectivamente. Sabendo-se que a taxa de juros cobrada pelo credor é de 2,5% ao mês, quanto deverá ser pago hoje para liquidar a dívida?

Fluxo de Caixa:

Observação: o prazo das parcelas foi transformado para meses, tendo em vista o prazo da taxa.

Solução: Para resolvermos a questão, devemos calcular o capital equivalente, na data atual, aos três pagamentos que compõem a dívida. Assim, o valor a ser pago será igual a soma das parcelas descapitalizadas para a data de hoje:

Interpretando a resposta: a empresa deverá pagar, na data de hoje, R$ 5.688,54, que é o capital equivalente as três parcelas da dívida original.

Tela 56
Módulo IV - Capitalização, Descapitalização e Equivalência de Capitais
3) Uma pessoa irá precisar de R$ 1.000,00 daqui a três meses e de R$ 2.200,00 daqui a seis meses. Considerando que um banco oferece 1,5% ao mês para uma determinada opção de investimento, quanto esta pessoa deverá depositar hoje para ter os valores de que necessitará?

Fluxo de Caixa:

Solução: O depósito que será efetuado hoje deverá ser equivalente à soma dos R$ 1.000,00 daqui a três meses e dos R$ 2.200,00 daqui a seis meses, então:

PV = 1.000/(1+0,015)3 + 2.200/(1+0,015)6 = 2.968,31


Interpretando a resposta: a pessoa deposita R$ 2.968,31 hoje, estes recursos sofrem juros de 1,5% durante três meses, chegando ao terceiro mês a R$ 3.103,90, onde será efetuado o pagamento de R$ 1.000,00. O saldo, de R$ 2.103,90, irá receber juros de 1,5% do quarto até o sexto mês, momento o qual será de R$ 2.200,00, exatamente o valor que deverá ser pago.

Tela 57
Módulo IV - Capitalização, Descapitalização e Equivalência de Capitais
4 - Usando o Excel

Devido àinfinidade de problemas que podem envolver o conceito de equivalência de capitais, torna-se praticamente impossível a construção de uma planilha única que sirva a todas as questões do gênero.

Nesse sentido, o aluno deve estar ciente de que a solução de problemas que envolvem esse assunto compreende nada mais do que o uso das fórmulas de valor presente e de valor futuro, aprendidas no módulo anterior, que servem em última análise, para capitalizar e descapitalizar valores ao longo do tempo.

Não obstante estas dificuldades desenvolverão a seguir uma planilha exemplo que servirá para o cálculo do valor presente de uma série de fluxos de caixa com até doze fluxos.

Lembramos que o conceito de “valor presente” se refere ao valor de determinado fluxo em uma data focal determinada que, não necessariamente, será a data atual ou zero, mas a data escolhida para a análise dos valores.

Aconselhamos, ainda, que na solução de problemas envolvendo equivalência de capitais, o aluno construa o fluxo de caixa representativo da questão, a fim de facilitar o desenvolvimento dos procedimentos de cálculo.


Tela 58
Módulo IV - Capitalização, Descapitalização e Equivalência de Capitais
Para construir a Planilha Exemplo siga as indicações:


1. Abra uma pasta nova que depois poderá ser arquivada com o nome de Equivalência de Capitais;

2. Na célua B2 escreva: Capitalização e Descapitalização;

3. No intervalo B4:B6, digite os títulos “Taxa”, “Data Focal” e “Valor Presente”;

4. Usando os recursos de formatação do Excel, formate as células C4 como percentuais e C6 como moeda (R$), ambas com duas casas decimais;

5. Na célula C6 digite: =SOMA(D10:D21);

6. No intervalo B8:D8, coloque os títulos “Data”, “Fluxo” e “Capitalização/”;

7. Na célula D9 encreva “Descapitalização”;

8. No intervalo B10:B21 digite as datas de 1 a 12;

9. Usando os recursos de formatação do Excel, formate os intervalos C10:D21 e D10:D21 como moeda (R$), com duas casas decimais.

10. Na célula D10 digite:

=SE(B10<$C$5;C10/(1+$C$4)^(B10-$C$5);C10*(1+$C$4)^($C$5-B10))

A condição acima estabelece que:

SE for cumprida a condição lógica B10<$C$5 (data em B10 menor do que a data em C5);

ENTÃO calcule C10/(1+$C$4)^(B10-$C$5) (descapitalize) e apresente o resultado na célula D4

SENÃO calcule C10*(1+$C$4)^($C$5-B10) (capitalize) e apresente o resultado na célula D4

11. Com o cursor na célula D10 selecione EDITAR, COPIAR;

12. Coloque o cursor na célula D11 clique com o mouse, arraste o cursor até a célula D21, solte o mouse e tecle enter.

13. Com esse último comando, a fórmula digitada em D10 é assumida para o intervalo de D11 a D21.

A figura abaixo representa a planilha construída mediante os procedimentos descritos acima:

Tela 59
Módulo IV - Capitalização, Descapitalização e Equivalência de Capitais
Resumo

A CAPITALIZAÇÃO e a DESCAPITALIZAÇÃO de valores ao longo do tempo são de fundamental importância para a solução de problemas envolvendo a matemática financeira.

Como capitalização, podemos entender o processo que visa calcular o valor de uma determinada quantia de dinheiro em uma data futura, mediante o acréscimo de juros. De maneira inversa, a descapitalização consiste em retirar os juros embutidos em valores que ocorrerão no futuro, visando trazê-lo a uma data anterior a sua ocorrência.

Esses procedimentos possibilitam a comparação de valores que ocorrem em momentos distintos no tempo, sem os quais se torna inviável sua comparação.

Ao acrescentarmos o conceito de equivalência de capitais, também chamada de equivalência financeira, sintetizamos os fundamentos básicos da disciplina, que servem para atinjir seu principal objetivo: o estudo do valor do dinheiro ao longo do tempo.
A figura e as fórmulas abaixo resumem os principais conceitos abordados no módulo:

Capitalização:

RCC => FV=PVx(1+i)n
RCS => FV=PVx(1+i x n)

Descapitalização:

RCC => PV=FVx1/(1+i)n
RCS => PV=FVx1/(1+i x n)