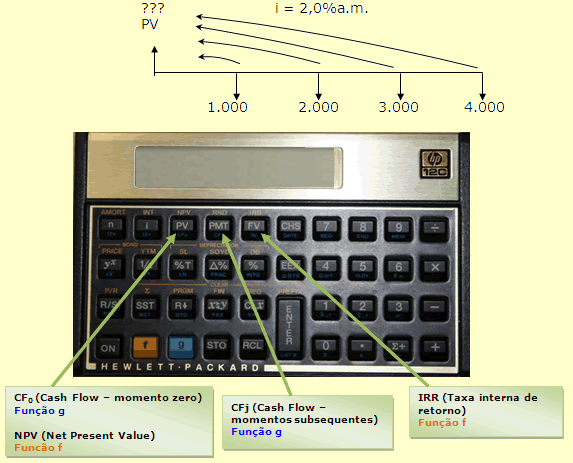
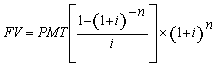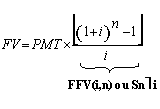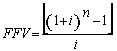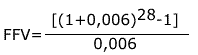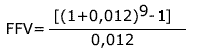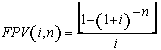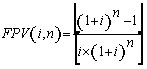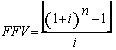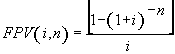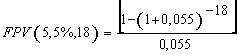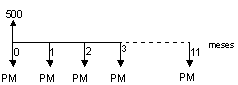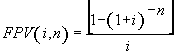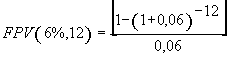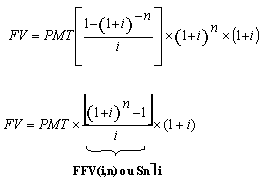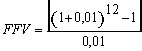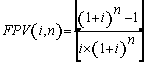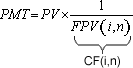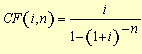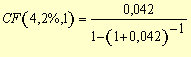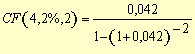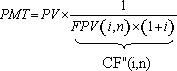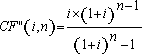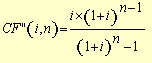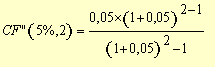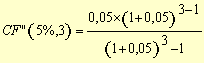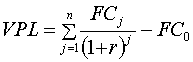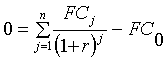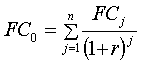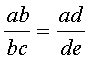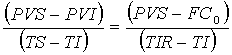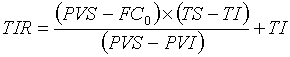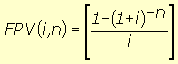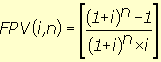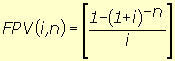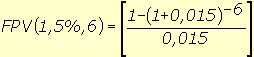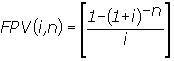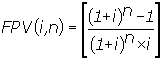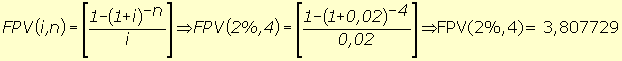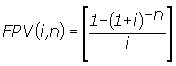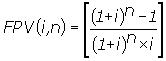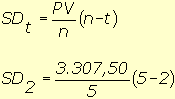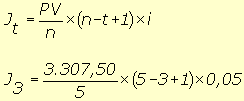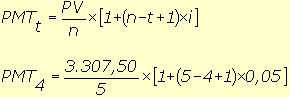3
- Sistema de Amortização Misto (SAM)
Desenvolvido
originalmente para as operações de financiamento do Sistema
Financeiro de Habitação – SFH, constitui-se da média
aritmética entre o Sistema Francês (SFA) e o Sistema de
Amortização Constante (SAC).
Para a
elaboração do plano de pagamentos, devemos somar os valores
obtidos pelo SAF e SAC e dividir o resultado por dois.
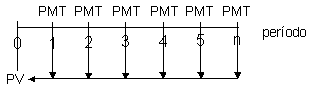
Exemplo:
Suponha um empréstimo no valor de R$ 1.500,00 realizado a uma
taxa de juros de 3% ao mês, em quatro parcelas.
1 º
Passo: Construir a tabela pelo SFA e pelo SAC, onde:
Pelo SFA:
Mês |
Saldo
Devedor |
Amortização |
Juros |
Prestação |
0 |
1.500,00
|
- |
- |
- |
1 |
1.141,46 |
358,54
|
45,00
|
403,54 |
2 |
772,16 |
369,30 |
34,24 |
403,54 |
3 |
391,78 |
380,38 |
23,16 |
403,54 |
4 |
-0,01 |
391,79 |
11,75 |
403,54 |
Observação!
O resíduo de -0,01, decorrente do arredondamento das parcelas,
geralmente são abatidos na última prestação.
Pelo SAC:
Mês |
Saldo
Devedor |
Amortização |
Juros |
Prestação |
0 |
1.500,00
|
- |
- |
- |
1 |
1.125,00 |
375,00 |
45,00
|
420,00 |
2 |
750,00 |
375,00 |
33,75 |
408,75 |
3 |
375,00 |
375,00 |
22,50 |
397,50 |
4 |
0,00 |
375,00 |
11,25 |
386,25 |
2º
Passo: Dado que o SAM constitui-se na média aritmética
do SAF e SAC, se pegarmos cada uma das células das tabelas dos
dois sistemas, somarmos e dividirmos por dois encontraremos a tabela
do SAM, onde:
Mês |
Saldo
Devedor |
Amortização |
Juros |
Prestação |
0 |
1.500,00
|
- |
- |
- |
1 |
1.133,23 |
366,77 |
45,00
|
411,77 |
2 |
761,08 |
372,15 |
34,00 |
406,15 |
3 |
383,39 |
377,69 |
22,83 |
400,52 |
4 |
-0,01 |
383,40 |
11,50 |
394,90 |
|
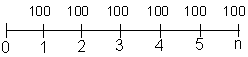
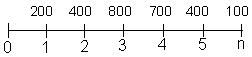

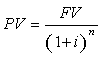
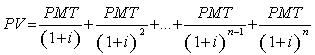
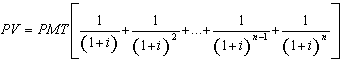
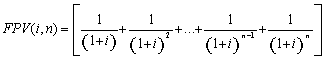
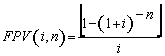
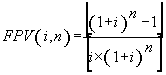
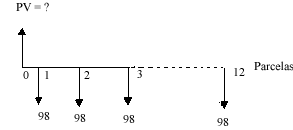

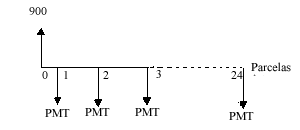
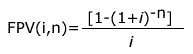
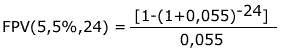
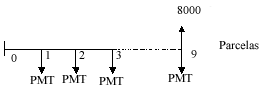
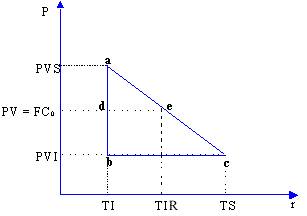
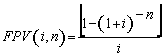 (7), substituindo-se FPV (i,n) da expressão (7) na fórmula
(10) e resolvendo a equação teremos:
(7), substituindo-se FPV (i,n) da expressão (7) na fórmula
(10) e resolvendo a equação teremos: