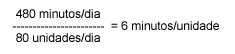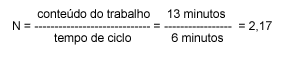• minimizar os custos de manuseio e movimentação interna de materiais;
• utilizar o espaço físico disponível de forma eficiente;
• apoiar o uso eficiente de mão de obra, evitando que esta se movimente desnecessariamente;
• facilitar a comunicação entre as pessoas envolvidas na operação, quando adequado;
• reduzir tempo de ciclo dentro da operação, sempre que possível, garantindo fluxos mais linearizados e coerentes com a estratégia;
• facilitar a entrada, saída e movimentação dos fluxos de pessoas e de materiais;
• facilitar manutenção de recursos, garantindo fácil acesso;
• facilitar acesso visual às operações, quando adequado;
• encorajar determinados fluxos (por exemplo, os arranjos físicos de alguns supermercados podem induzir fluxos de clientes de forma a aumentar a exposição dos produtos a eles).

• Arranjo físico é, muitas vezes, uma atividade difícil e de longa duração, em virtude das dimensões físicas dos recursos de transformação movidos.
• O rearranjo físico de uma operação existente pode interromper seu funcionamento suave, levando à insatisfação do cliente ou a perdas na produção.
• Se o arranjo físico (examinado a posteriori) está errado, pode levar a padrões de fluxo excessivamente longos ou confusos, estoque de materiais, filas de clientes, tempos de processamento desnecessariamente longos, operações inflexíveis, fluxos imprevisíveis e altos custos.

1. o produto a ser fabricado;
2. a quantidade a ser fabricada;
3. os roteiros de produção ou sequências de operações utilizadas;
4. os serviços de suporte ou funções auxiliares que devem suprir o fluxo em questão;
5. o tempo dispendido na produção; quando deve ser produzido, e em que frequência.
6. quando deve ser produzido, e em que frequência.

• Arranjo físico por produto ou linear: corresponde ao sistema de produção contínua (como as linhas de montagem e as indústrias de processo);

• Arranjo físico por processo ou funcional: corresponde ao sistema de produção de fluxo intermitente (como a produção por lotes ou encomendas);

• Arranjo físico de posição fixa ou posicional: corresponde ao sistema de produção em projetos;

• Arranjo físico celular: o objetivo desse arranjo físico é montar minifábricas dentro da fábrica.

EXEMPLO

Qual das afirmações abaixo é falsa :

1 - O arranjo físico recomendado para uma padaria é por processo ou funcional;
2 - Uma fábrica de sapatos pode utilizar o arranjo físico por produto ou em linha;
3 - Um banco deve utilizar um arranjo físico por produto;

SOLUÇÃO

Para responder essas questões, inicialmente, deve-se identificar qual o tipo de sistema de produção para cada processo.

Numa PADARIA o SISTEMA DE PRODUÇÃO É DE FLUXO INTERMITENTE, pois temos vários produtos produzidos e vendidos, e que são organizados de acordo com a função, de tal modo que um ARRANJO FÍSICO POR PROCESSO ou FUNCIONAL é recomendado.

Numa FÁBRICA DE SAPATOS podemos produzir UM ÚNICO MODELO OU POUCOS MODELOS COM PEQUENAS VARIAÇÕES cujo SISTEMA DE PRODUÇÃO É CONTÍNUA OU EM LINHA, logo o ARRANJO FÍSICO mais indicado é POR PRODUTO OU EM LINHA.

Por outro lado, se houver grandes variações nos modelos, ou seja, VÁRIOS MODELOS sendo produzidos onde várias sequências distintas podem existir, nesse caso, O SISTEMA DE PRODUÇÃO É DE FLUXO INTERMITENTE e O ARRANJO FÍSICO mais recomendado é POR PROCESSO OU FUNCIONAL.

NUM BANCO existem vários produtos (serviços) oferecidos aos clientes, desde pagar conta, fazer aplicações, pedir orientação, etc, nesse caso, O SISTEMA DE PRODUÇÃO É DE FLUXO INTERMITENTE e o ARRANJO FÍSICO RECOMENDADO É O FUNCIONAL OU POR PROCESSO.
LOGO, A AFIRMATIVA FALSA É A 3

1. escolhem o que vão comer olhando para o menu luminoso na parede;
2. entram na fila do caixa;
3. fazem o pedido;
4. aguardam o pedido ser atendido;
5. pagam o serviço;
6. vão à mesa;
7. comem;
8. levam suas embalagens ao lixo;
9. deixam o local.

(a) produtos fabricados em grandes quantidades;
(b) produtos semelhantes entre si;
(c) equipamentos dedicados;
(d) utilizados em sistemas de produção contínuos;
(e) produção e controle da produção mais simplificado;
(f) exige balanceamento da linha de produção;
(g) equipamentos dispostos de acordo com a sequência de operações.

Suas características são:

(a) máquinas e equipamentos fixos, em que o produto se movimenta;
(b) produtos e roteiros muito variados;
(c) utilizados em sistemas de produção intermitente;
(d) máquinas e equipamentos agrupados por função (soldagem, montagem, usinagem etc.);
(e) equipamentos de média flexibilidade;
(f) programação e controle da produção mais complexa;
(g) problemas de qualidade detectados após a produção do lote inteiro;
(h) formação de filas de lotes nas máquinas (conforme esquema a seguir).

(a) o volume de material transportado até o local de aplicação;
(b) as dimensões da unidade de movimentação;
(c) o método de transporte;
(d) a quantidade de percursos até o local de aplicação;
(e) a origem e o destino do material transportado;
(f) o acesso ao local de aplicação;
(g) a disponibilidade de equipamentos adequados para a
movimentação.

• arranjo físico por produto;

• arranjo físico por processo;

• arranjo físico posicional;

• arranjo físico celular.

1. uma estimativa da demanda ou da venda; e
2. uma estimativa do erro de previsão esperado, pois desta estimativa derivarão importantes decisões sobre os “colchões” de segurança que serão dimensionados para a operação.

1. Método Delphi. O processo Delphi é interativo e permite que especialistas, às vezes localizados em pontos distantes entre si, incorporem o consenso de suas opiniões subjetivas ao processo de previsão. Comumente se envolvem de 6 a 12 especialistas no processo. Consiste nos seguintes passos: em primeiro lugar, propõe-se ao grupo determinada pergunta bem específica sobre alguma variável que se queira prever. Em seguida, coletam-se as várias opiniões, de forma sigilosa e individual. O coordenador do processo trata essas opiniões, estatisticamente, e retorna o resultado aos participantes. Estes são, então, solicitados a refazer suas estimativas. Recolhem-se e realimentam-se interativamente as opiniões e elas são tratadas até que o processo de convergência das opiniões atinja um nível desejado.
2. Júri de executivos. Esse método procura capturar a opinião de pequenos grupos, em geral, de executivos de nível alto sobre alguma variável que pretenda prever.
3. Força de vendas. Nessa abordagem, cada vendedor ou representante de força de vendas emite uma estimativa do volume de vendas para seus territórios. As previsões de cada vendedor são agregadas para formar uma previsão geral para a empresa.
4. Pesquisa de mercado. Esse método solicita diretamente dos possíveis clientes ou consumidores sua intenção de compra futura (“Quantas horas de Internet você pretende utilizar nos três próximos meses?”)
5. Analogia histórica. Esse método qualitativo procura identificar produtos similares dos quais se possuem dados para, por analogia, melhor estimar, por exemplo, um produto novo.

(a) a previsão é sempre obtida por meio de algum tipo de média, que leva em consideração valores reais anteriores da demanda;
(b) ao contrário do que acontece com as regressões, só é possível prever um período à frente, embora se possam conceber adaptações para obter maior número de previsões futuras;
(c) as médias são móveis, o que significa que, a cada nova previsão, são abandonadas, ou mais fracamente ponderados os valores mais antigos da demanda real e incorporados os mais novos.

• Média aritmética - reflete o comportamento médio de um período, sem considerar tendências. Admitindo-se os seguintes dados:

A média aritmética será o resultado da divisão do somatório das vendas pelo número de anos:

média = vendas/n = (20+22+24+26+24+26+26+28+28+30+32)/11 = 26

• Média móvel simples – considera-se um período restrito de tempo e calcula-se a projeção para o período imediato, ou seja, a previsão para o período t, imediatamente futuro, é obtida tomando-se a média aritmética dos n valores reais da demanda imediatamente passados.

Inicialmente, deve-se escolher o valor de n. Essa escolha é relativamente arbitrária. Como regra geral, quanto maior n, mais os efeitos sazonais serão suavizados. Supõe-se para o exemplo acima n=3, o que implica dizer que a demanda prevista para qualquer mês será sempre a média aritmética das demandas reais dos três últimos meses.

Dois casos particulares merecem destaque:

• Se n = 1 a previsão se resume em tomar simplesmente o valor da última demanda real verificada;

• Se n = 12, significa anular completamente todos os efeitos sazonais, distribuídos ao longo do ano.

O método da média móvel simples pode ser eficiente quando a demanda é estacionária, ou seja, quando ela varia em torno de um valor médio.

Para demandas crescentes ou decrescentes ao longo do tempo, a tendência é que a previsão fornecida pelo método esteja sempre em atraso, em relação aos valores reais.

• Média móvel ponderada - esse método possui em comum com o método da média móvel simples, a escolha de n valores reais anteriores da demanda, para a composição da média. Diferentemente da MMS, os valores recebem pesos diferentes, geralmente refletindo a maior importância dada aos valores mais recentes da demanda.

No exemplo anterior, poder-se-ia adotar os pesos 0.2, 0.3 e 0.5 (nesse caso n = 3) para demandas reais de julho, agosto e setembro, respectivamente. A previsão para outubro seria:

Previsão (outubro) = 0.2 (12) + 0.3(15) + 0.5(14) = 13.9

• Média móvel exponencialmente ponderada de 1ª ordem - esse modelo é mais sofisticado e muito mais utilizado do que os dois anteriores. A previsão atinge, em princípio, apenas um período imediatamente à frente.

Fonte: Tubino, Dalvio Ferrari. Manual de Planejamento e Controle da Produção. São Paulo: Ed. Atlas, 1997, p.76.

A previsão para o período t é dada por uma fórmula empírica:

que se interpreta como: a previsão para o período t é igual à previsão para o período (t–1). Em termos simbólicos, pode-se escrever:

Exemplo: Retomemos o mesmo exemplo que foi utilizado e ilustrado anteriormente. Assumindo a demanda prevista de junho igual a 10 (coincidente, pois, com o valor real) e adotando a = 0.3, podemos montar os cálculos abaixo:

Cálculos:

D julho = D junho + a ( Y junho - D junho ) = 10 + 0,3( 10 – 10 ) = 10

D agosto = D julho + a ( Y julho - D julho ) = 10 + 0,3( 12 – 10 ) = 10,6

D setembro = D agosto + a ( Y agosto - D agosto ) = 10.6 + 0,3( 15 – 10.6 ) = 11,9

D outubro = D setembro + a ( Y setembro - D setembro ) = 11.9 + 0,3( 14 – 11.9 ) = 12.5

Lembrando que a finalidade última do modelo é a previsão, é fundamental que se tenha uma série de valores reais passados da demanda à qual o modelo possa ser aplicado. A posse dessa série permite tanto a fixação de um valor inicial para a previsão como a escolha da constante a.

Há pelo menos duas maneiras práticas para se fixar o valor inicial da demanda prevista (a qual não pode ser dada pelo modelo).

• A primeira considera que o valor inicial da demanda é igual ao valor real da demanda da série, uma vez que, se a série de dados passados for suficientemente longa, esse critério não terá qualquer influência nas previsões futuras.

• Outra prática consiste em se tomar como previsão inicial a média aritmética de k valores reais, imediatamente passados da demanda. Não há uma regra definitiva quanto ao valor de k, mas costuma-se usar a seguinte fórmula:

k = (1/ a) – 1

Quanto ao valor de a , ele é normalmente obtido por tentativas, de acordo com as seguintes etapas:

• aplicam-se vários valores de a aos dados existentes, obtendo-se então várias séries previsões; o valor de a varia geralmente entre 0 (zero) e 1(um);

• para cada conjunto de previsões, correspondente a um certo a, calcula-se uma medida do erro total da previsão em relação aos valores reais;

• escolhe-se o valor de a , que fornece as previsões com o menor erro total associado.

Métodos da regressão por mínimos quadrados - interpreta a série numérica por meio da construção de uma reta. Identifica-se o comportamento médio da série que, a partir da reta resultante, permite realizar as projeções desejadas.

Exemplo:

A tabela abaixo mostra as vendas anuais da fábrica XYZ Ltda.
Estime a previsão de vendas para o 12º ano.

Sendo Y = a + b X a equação da reta em que:

Y = a variável dependente (que será prevista)
a = o ponto de intercessão da reta com o eixo y
b = a inclinação da reta
X = a variável independente

CÁLCULO
X	Y	XY	X2
0	30	0	0
1	40	40	1
2	38	76	4
3	38	114	9
4	53	212	16
5	50	250	25
6	50	300	36
7	57	399	49
8	62	496	64
9	60	540	81
10	62	620	100
X = 55	Y = 540	X Y= 3047	X2= 385

Substituindo os valores assim obtidos nas equações normais, tem-se, lembrando que n = 11

540 = 11 a + 55 b (*)
3047 = 55 a + 385 b ( ** )

O sistema de duas equações e duas incógnitas resultante pode ser resolvido multiplicando-se a equação ( * ) por (-5) e a adicionarmos à equação ( **)

Substituindo o valor de b na equação (*) original, tem-se:

a = (540 – 55b)/11 = (540 – 173.8)/11 = 33.318 => a = 33.318

A equação da reta que melhor representa os pontos dados é:

Y = 33.318 + 3.1545 X

Pode-se ter uma primeira ideia da adequação com que a reta permite prever futuros valores de Y, desde que conhecidos os correspondentes valores de X. Por exemplo, se quisermos o valor estimado de Y para X = 3 (valor real de Y é 38) teremos:

Y = 33.318 + 3.1545*3 = 42.78

Valores reais e previstos

Resumo

Um modelo genérico de previsão e manutenção dos dados relativos à demanda é composto por cinco passos, a saber: objetivo, coleta e análise dos dados, seleção da técnica de previsão, obtenção das previsões e monitoramento do modelo.

Os modelos de previsão de demanda classificam-se em qualitativos e quantitativos. Os modelos apresentados e exemplificados fundamentam-se em técnicas quantitativas.

As técnicas das médias simples, ponderadas e exponencialmente ponderadas usam dados históricos para calcular uma média das demandas passadas. Essa média é usada como estimativa.

A técnica de regressão linear por mínimos quadrados estabelece relação entre variáveis. Uma variável é conhecida ou assumida, e usada para prever o valor de uma variável desconhecida. Dados antigos estabelecem uma relação funcional entre as duas variáveis.

Reduzir custos operacionais requer que sejam reduzidos:

• os estoques de produtos acabados,
• de matérias-primas e
• de material em processo.

Por sua vez, atingir a produtividade desejada de pessoas e máquinas pode exigir um grau de ocupação desses recursos que pode levar ao aumento dos estoques. Finalmente, manter ou melhorar o nível de atendimento aos clientes pode também levar ao aumento de estoques, notadamente se a demanda for muito flutuante. Evidentemente, exige-se um balanço e um compromisso finais entre os vários objetivos, que dificilmente poderão ser totalmente atendidos ao mesmo tempo.

Dá-se o nome de Plano Mestre de Produção - PMP - ao documento que diz quais itens serão produzidos, e quanto de cada item, para determinado período. Geralmente, esse período cobre algumas poucas semanas, podendo chegar a seis meses ou mesmo um ano. O PMP deverá ter aspecto simplificado como demonstra a quadro "Aspecto do plano mestre de produção semanas".

A partir do momento em que o plano mestre de produção diz o que será feito – quais os produtos e quanto de cada um deles –, começa então o problema de programar e controlar a produção para segui-lo; para tal, estão disponíveis técnicas e métodos.

3 - Programação para sistemas de volume intermediário

É o sistema em que os diversos produtos são feitos na mesma linha de produção, tal como acontece com bebidas, cigarros, refrigeradores, aparelho de som etc.

Toda vez que um produto é programado, é necessária mudança nas linhas, isto é, novo ajuste e preparação de máquinas. Para que isso ocorra, duas perguntas devem ser respondidas:

1. quanto produzir de cada produto?
2. em que ordem devem ser produzidos os produtos?

A resposta à pergunta quanto produzir pode ser dada de muitas formas, pois não faltam critérios específicos de cada empresa, baseados no bom senso ou em razões de ordem histórica. A teoria elementar dos custos associados aos estoques fornece a quantidade a fabricar que leva em conta, de um lado, os custos de preparação de máquinas para uma rodada de produção e, de outro, os custos de manter o produto em estoque. Esses dois custos são antagônicos: para se gastar menos com a preparação de máquinas é preciso diminuir o número de rodadas de produção, o que, para um dado nível de demanda, leva ao aumento na quantidade fabricada de cada vez e, consequentemente, nos estoques mantidos. Esse aumento nos estoques fará aumentar o custo de manutenção associado.

Entretanto, se os dois custos – preparação de máquinas e manutenção de estoques, forem somados, é possível determinar uma quantidade a produzir que minimize a soma. Essa quantidade é chamada Lote Econômico de Fabricação (LEF) e constitui possível resposta à pergunta de quanto produzir de cada produto que utiliza a linha.

Uma técnica usada para o sequenciamento é o chamado o Tempo de Esgotamento (TE). Dado um produto candidato ao sequenciamento, o seu Tempo de Esgotamento é definido como:

em que a taxa de consumo é a quantidade média consumida no intervalo de tempo (dia, semana, mês etc.).

Se tivermos 3000 unidades de um produto estoque, por exemplo, e a sua taxa de consumo for de 800 unidades por semana, o seu Tempo de Esgotamento será de:

TE = 3000/800 = 3,75 semanas

O Tempo de Esgotamento é medida da urgência com que o produto deve ser fabricado: quanto menor o TE, mais cedo o produto estará em falta. Portanto, quando existirem vários produtos aguardando processamento na mesma linha, programa-se primeiro o produto com menor Tempo de Esgotamento.

Tão logo termine o processamento do produto escolhido, os cálculos devem ser refeitos para que se determine o novo produto a ser sequenciado.

Solução

O quociente do estoque disponível pela taxa de consumo nos dará o valor do Tempo de Esgotamento TE para cada um dos produtos. Repete-se a tabela abaixo já com os tempos de esgotamento na última coluna.

Final da semana 1

Ao final da semana 2.5 (ou seja, 1 + 1.5), quando termina o processamento do produto do produto III, os valores dos estoques terão novamente se alterado; como o tempo decorrido desde o último cálculo foi de 1,5 semanas (quanto durou o processamento do produto III), o consumo foi proporcional a esse tempo. Assim, por exemplo, do II foram consumidas 1800 unidades (1.200 x 1,5). Todos os cálculos refeitos até o final da semana 2,5 estão na tabela seguinte:

Final da semana 2.5

Uma nova tabela mostraria que o produto II será o próximo a ser processado, sendo que esse processamento estará terminado ao final da semana 3,5.

1. como será a alocação de carga entre os centros de trabalho?
2. como será o sequenciamento dessas operações num dado centro ao qual a carga já foi alocada?

• Tempo de processamento (TP)
• Tempo de espera (TE)
• Tempo de término (TT)
• Data devida (DD)
• Atraso (AT)

• o tempo de espera;
• o tempo de término
• o atraso.

Trabalho	Tempo de Processamento (TP)	Data Devida (DD)
A	5	14
B	8	9
C	2	10
D	4	20
E	1	7

Solução

Da maneira como são definidas as grandezas procuradas, devemos calcular, progressivamente: tempo de espera, tempo de término e o atraso de cada trabalho. Os cálculos resumem-se no seguinte:

A regra de sequenciamento ilustrada pelo exemplo é chamada Regra PEPS. É a regra dominante em atividades de serviço.

A linha de montagem representa o caso clássico do fluxo de operações em um sistema contínuo. Na linha de montagem, o produto (ou parte dele) é dividido em certo número de operações (ou tarefas) que devem ser distribuídas por postos de trabalho. O posto de trabalho é ocupado por uma ou mais pessoas; mesmo que haja uma só pessoa no posto de trabalho, mais de uma tarefa ou operação pode ser alocada ao posto.

Embora a sequência de operações seja fixa, a sua designação a postos de trabalho pode ser mais eficiente ou menos eficiente, no sentido de melhor ou pior aproveitamento do tempo disponível em cada posto. A tarefa do balanceamento de linha é atribuir as tarefas aos postos de trabalho de forma a atingir uma dada taxa de produção e de forma que o trabalho seja dividido igualmente entre os postos.

Por outro lado, a figura abaixo apresenta o chamado Diagrama de Precedências, que facilita a visualização da ordem em que as tarefas devem ser completadas. No Diagrama de Precedências, as tarefas são apresentadas por círculos, unidos por retas que simbolizam a precedência. Ao lado de cada círculo, coloca-se a duração da tarefa correspondente.