Solução
4
a1) retorno
esperado para cada ativo isolado:
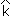 F
= (16 + 17 + 18 + 19)/4 F
= (16 + 17 + 18 + 19)/4
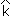 F
= 17,5% F
= 17,5%
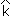 G
= (17+16+15+14)/4 G
= (17+16+15+14)/4
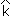 G
= 15,5% G
= 15,5%
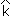 H
=(14 +15+16+17)/4 H
=(14 +15+16+17)/4
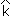 H
= 15,5% H
= 15,5%
a2) Variância
e desvio-padrão dos retornos esperados:
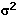 kF
= {[(16 – 17,5)2 + (17 – 17,5)2 + (18
– 17,5)2 + (19 – 17,5)2]/4}/10.000 kF
= {[(16 – 17,5)2 + (17 – 17,5)2 + (18
– 17,5)2 + (19 – 17,5)2]/4}/10.000
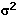 kF
= 0,000125 kF
= 0,000125
 kF
= kF
= 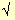 0,000125 0,000125
 kF
= 0,01118 kF
= 0,01118
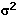 kG
={[(17 – 15,5)2 + (16 – 15,5)2 + (15
– 15,5)2 + (14 – 15,5)2]/4 }10.000 kG
={[(17 – 15,5)2 + (16 – 15,5)2 + (15
– 15,5)2 + (14 – 15,5)2]/4 }10.000
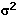 kG
= 0,000125 kG
= 0,000125
 kG
= kG
= 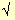 0,000125 0,000125
 kG
= 0,01118 kG
= 0,01118
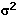 kH
={[(14 – 15,5)2 + (15 – 15,5)2 + (16
– 15,5)2 + (17 – 15,5)2]/4 }/10.000 kH
={[(14 – 15,5)2 + (15 – 15,5)2 + (16
– 15,5)2 + (17 – 15,5)2]/4 }/10.000
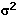 kH
= 0,000125 kH
= 0,000125
 kH
= kH
= 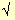 0,000125 0,000125
 kH=
0,01118 kH=
0,01118
4b) covariância
e coeficiente de correlação linear:
CovG,H
= {[(17 -15,5) . (14 – 15,5) + (16 -15,5) . (15 – 15,5) +
(15 – 15,5) . (16 – 15,5) + (14 – 15,5).(17 –
15,5)]/4}/10.000
CovG,H = -0,000125
Observe que:
• No Ano 1, enquanto o retorno esperado do Ativo G se apresenta
acima do retorno médio esperado (17% >15,5%), no Ativo H, o
retorno esperado se apresenta abaixo da média (14% < 15,5%),
logo, os retornos esperados se apresentam em sentidos contrários,
enquanto um anda acima da sua média, o outro anda abaixo da sua
média, portanto, a correlação é negativa (isto
é ótimo).
• No Ano 2,
enquanto o retorno esperado do ativo G anda acima da média (16%
> 15,5%), o retorno estimado para o ativo H anda em sentido contrário
(15% < 15,5%), ou seja, ambos os retornos esperados se comportam em
sentido contrário ao das suas médias, logo, novamente estamos
diante de uma correlação negativa, o que é muito
bom. Deve-se sempre perseguir correlação negativa.
• O mesmo processo
pode ser observado para o Ano 3 e para o Ano 4. Em muitas situações,
como neste exemplo, se percebe o sinal da covariância sem ser necessário
o cálculo, basta olhar o comportamento dos retornos esperados ou
observados com seus respectivos retornos médios esperados ou observados.
rGH = -0,000125/0,01118
x 0,01118
rGH = -1,0 (correlação perfeitamente negativa)
CovF,G = {[(17 -15,5) . (16 – 17,5) + (16 -15,5) . (17
– 17,5) + (15 – 15,5) . (18 – 17,5) + (14 – 15,5).(19
– 17,5)]/4}/10.000
CovF,G = -0,000125
rF,G = -0,000125/0,01118 x 0,01118
rF,G = -1,0 (correlação perfeitamente negativa)
CovF,G
= {[(14 -15,5) . (16 – 17,5) + (15 -15,5) . (17 – 17,5) +
(16 – 15,5) . (18 – 17,5) + (17 – 15,5).(19 –
17,5)]/4}/10.000
CovF,G = 0,000125
Observe que:
Ano 1: tanto o retorno
esperado de F quanto o retorno esperado de H andam no mesmo sentido (correlação
positiva), isto é, ambos operam abaixo das suas respectivas médias.
Ano 2: assim como
ocorreu no Ano 1, ambos os retornos esperados estão andando abaixo
das respectivas médias, ou seja, andando no mesmo sentido (correlação
positiva);
Ano 3: ambos os retornos
esperados estão andando acima das suas respectivas médias
(18% >17,5%) e (17% >15,5%), novamente, correlação
positiva.
Ano 4: idem o observado
no Ano 3.
rF,H = 0,000125/0,01118 x 0,01118
rF,H = 1,0 (correlação perfeitamente positiva)
Veja que o sinal do coeficiente é igual ao sinal da covariância.
4c) cálculo
do retorno de cada carteira/desvio-padrão de cada carteira:
Carteira 40% de G
e 60% de H
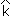 P
= (0,40 x 15,5) + (0,60 x 15,5) P
= (0,40 x 15,5) + (0,60 x 15,5)
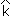 P
= 15,5% P
= 15,5%
 PG,H
= PG,H
=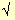 0,42
x 0,000125 + 0,62 x 0,000125 + 2,0 x 0,4 x 0,6 x -0,000125 0,42
x 0,000125 + 0,62 x 0,000125 + 2,0 x 0,4 x 0,6 x -0,000125
 PG,H
= 0,0022 x 100 PG,H
= 0,0022 x 100
 PG,H
= 0,22% PG,H
= 0,22%
Média ponderada
dos desvios-padrão dos ativos individuais
MP = (0,4 x 1,118) + (0,6 x 1,118)
MP = 1,118%
Percebemos que a diversificação
reduziu muito o risco, pois, na carteira com dois ativos, o risco total
é igual a 0,22%, enquanto a média ponderada dos desvios
padrão dos títulos individuais alcançou 1,118%. O
motivo para esta queda significativa do risco deve-se ao fato de estarmos
diante de uma dupla de ativos que apresenta correlação perfeitamente
negativa.
Carteira 60% de F
e 40% de G
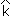 P
= (0,60 x 17,5) + (0,40 x 15,5) P
= (0,60 x 17,5) + (0,40 x 15,5)
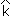 P
= 16,7% P
= 16,7%
 PF,G
= PF,G
=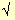 0,62
x 0,000125 + 0,42 x 0,000125 + 2,0 x 0,6 x 0,4 x -0,000125 0,62
x 0,000125 + 0,42 x 0,000125 + 2,0 x 0,6 x 0,4 x -0,000125
 PF,G
= 0,22% PF,G
= 0,22%
Média ponderada
dos desvios-padrão dos ativos individuais
MP = (0,6 x 1,118) + (0,4 x 1,118)
MP = 1,118%
Novamente, em função
do par de ativos apresentarem um coeficiente de correlação
linear igual a -1,0, percebemos uma forte redução no risco
total medido pelo desvio-padrão, que passou de 1,118% para 0,22%.
Carteira 70% de F
e 30% de H
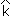 P
= (0,70 x 17,5) + (0,30 x 15,5) P
= (0,70 x 17,5) + (0,30 x 15,5)
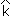 P
= 16,90% P
= 16,90%
 PF,G
= PF,G
=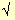 0,72
x 0,000125 + 0,32 x 0,000125 + 2,0 x 0,7 x 0,3 x 0,000125 0,72
x 0,000125 + 0,32 x 0,000125 + 2,0 x 0,7 x 0,3 x 0,000125
 PF,G
= 0,01118 x 100 PF,G
= 0,01118 x 100
 PF,G
= 1,118% PF,G
= 1,118%
Média ponderada
dos desvios-padrão dos ativos individuais
MP = (0,7 x 1,118) + (0,3 x 1,118)
MP = 1,118%
Neste caso, para qualquer
composição de carteira entre os ativos F e H, o desvio-padrão
dos retornos esperados da carteira será sempre igual à média
ponderada dos desvios-padrão dos retornos esperados dos títulos
individuais. Assim, seria indiferente colocar o dinheiro numa carteira
com apenas um ativo ou colocar o dinheiro numa carteira com dois ativos
diferentes porque o risco total (medido pelo desvio-padrão) não
sofreu nenhuma redução. Observe que neste par de ativos
o coeficiente de correlação linear é igual a 1,0.
Logo, somente diante
de pares de ativos com coeficiente de correlação linear
menor do que 1,0 é que será possível ocorrer diminuição
do risco total entre uma carteira com dois ativos diferentes e uma carteira
com ativo individual (isolado).
|




 %
%