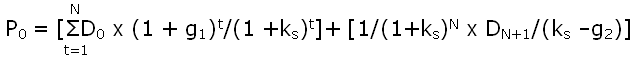Unidade 3 Módulo 1
Tela 1
Módulo 01 – Conceito de Custo de Capital

1 - Custo de Capital

Ao analisar o relatório que mostra a divulgação do resultado do 4T08 (4º trimestre de 2008) e 12MO8 da Grendene (www.grendene.com.br) somos informados de que a empresa investiu R$22,8 milhões em seu parque fabril durante o ano de 2008. De nada adianta a Grendene aumentar a sua capacidade de produção de calçados se a administração da empresa não souber dimensionar o custo das fontes de dinheiro que a Grendene utiliza em seus investimentos.

Um investimento no parque fabril irá exigir dinheiro não apenas para a compra do imóvel (terreno), da construção do(s) prédio(s), da compra do(s) equipamento(s), do treinamento da mão-de-obra, mas também recursos para atender a variação no ativo realizável operacional líquido ou na variação do capital de giro operacional líquido.

As fontes de dinheiro que a empresa utiliza normalmente têm como origem o patrimônio líquido e o passivo exigível oneroso. É função da administração da empresa estimar o custo de cada uma das fontes de dinheiro utilizada pela empresa. Depois de apurado o custo de cada fonte, será necessário apurar o peso de cada fonte, com isso, será possível calcular o custo de capital da empresa ou o custo médio ponderado de capital – CMPC- ou WACC (weighted average cost of capital).

Tela 2
Módulo 01 – Conceito de Custo de Capital

Suponha que a taxa de retorno dos projetos de determinada empresa seja de 15% ao ano. Será interessante que o custo de capital dessa empresa seja menor que 15% ao ano porque, desta forma, será possível a existência da maximização da riqueza do(s) proprietário(s) da empresa.

Vamos pensar numa S.A. de capital aberto, por exemplo, a Grendene. O capital social da Grendene poderá ser composto por ações ordinárias e ações preferenciais. Pode acontecer de ser somente por ações ordinárias. Mas não pode ser exclusivamente por ações preferenciais. Se ocorrer de existir os dois tipos de ações, será preciso apurar o custo das ações ordinárias e o custo das ações preferenciais. Vamos supor que a Grendene não distribua todo o seu lucro líquido, que ela sempre fique com uma parte desse lucro. Isso irá gerar lucros retidos, o que exige que se calcule o custo do lucro retido. Vamos imaginar que a Grendene esteja pensando em emitir novas ações, isso, por sua vez, irá provocar o cálculo do custo de emissão de novas ações.


Tela 3
Módulo 01 – Conceito de Custo de Capital

As empresas, em sua maioria, não vivem apenas do dinheiro oriundo do patrimônio líquido, é normal a participação de fundos vindos de banqueiros e, também, de investidores, portanto, teremos que calcular o custo da dívida nas empresas. Vamos começar pelo custo do patrimônio líquido.


Tela 4
Módulo 01 – Conceito de Custo de Capital

2 - Custo das Ações Ordinárias – KS

O que são ações?


Segundo Pinheiro (2001) ações são títulos de participação negociável, que representam parte do capital social de uma sociedade anônima, e conferem ao possuidor o direito de participação nos resultados da empresa.

Podem ser consideradas como certificado ou título de propriedade, representativo das partes do capital social de uma sociedade econômica. O acionista é, portanto, proprietário de uma parcela da empresa, correspondente ao número de ações que possui.

Existem, basicamente, dois tipos de ações:

1. Ordinária ou comum;

2. Preferencial.


Ordinária ou comum
É aquela que goza, em toda a plenitude, dos direitos de participação na administração da sociedade e nos resultados financeiros. Portanto, têm a característica básica do direito a voto. Na sociedade anônima, é por meio do voto que o acionista tem o direito legal de controle da organização.



Preferencial
É aquela que, em troca de determinados privilégios (preferência nos resultados da empresa) têm privado o seu direito de voto. Três são as preferências que o acionista detentor de ações preferenciais adquire:
• preferência na distribuição de resultados;
• preferência no reembolso de capital e
• preferência na acumulação dessas duas situações.

Tela 5
Módulo 01 – Conceito de Custo de Capital

Quando um investidor compra uma ação, ele poderá experimentar as seguintes situações:

• receber dividendos;
• experimentar ganho ou perda de capital.

No Brasil, além dos dividendos, o acionista poderá receber juros sobre o capital próprio.

De acordo com a Lei n. 10.303 de 31 de outubro de 2001, o número de ações preferenciais sem direito a voto, ou sujeitas à restrição no exercício desse direito, não pode ultrapassar 50% (cinqüenta por cento) do total das ações emitidas.

Lemes Júnior, Rigo e Cherobim (2002), veem o custo de capital da ação ordinária, ks, como o retorno exigido pelos acionistas comuns, por financiarem permanentemente a empresa.

Segundo Gitman (2004) o custo da ação ordinária pode ser medido, por exemplo, por meio de dois modelos, um deles é o CAPM (Modelo de Precificação de Ativos de Capital), o outro seria o Modelo de Gordon, também conhecido por modelo de avaliação com crescimento constante. Antes de estudar o modelo de Gordon, iremos estudar o modelo de crescimento nulo.


Tela 6
Módulo 01 – Conceito de Custo de Capital

3 - Modelo de crescimento nulo

Pense numa empresa de capital aberto, por exemplo: Companhia Vale do Rio do Doce, Petrobras, Gerdau, Natura, Grendene, Bradesco, Itaú, Banco do Brasil, Randon, Marcopolo, Lojas Renner etc. Imagine que no último ano uma dessas empresas pagou $1,0 de dividendos por ação. Inicialmente vamos imaginar que essa empresa irá pagar esse valor de dividendos para sempre, ou seja, todo ano o valor dos dividendos por ação será igual a $1,0, de forma perpétua. O que você deduz? Certamente que não irá ocorrer qualquer taxa de crescimento nos dividendos pagos pela empresa, logo, a taxa de crescimento dos dividendos será nula. Essa situação nos remete a um modelo de avaliação de ações, chamado Modelo de Crescimento Nulo.

Como representar o pagamento dos dividendos? O último dividendo se refere ao dividendo atual, portanto, será representado dessa maneira: D0. O próximo dividendo será representado dessa maneira: D1. O dividendo a ser pago no Ano 2 será representado por D2 e assim por diante.

No modelo de crescimento nulo nós temos que:


D0=D1=D2=D3=......D∞

Você está interessado em estimar o valor da ação da empresa. Pense agora como um investidor. Você está estudando a compra de ações de uma empresa, de imediato lhe vem à cabeça uma taxa de retorno desse papel. Essa taxa de retorno, k, certamente será de acordo com o risco do papel, quanto maior o risco, maior será o retorno exigido.

Precisamos agora pensar no valor da ação, ou seja, no preço corrente da ação, P0. Como apurar o preço corrente da ação?


Tela 7
Módulo 01 – Conceito de Custo de Capital

Equação do modelo de crescimento nulo:


P0 = D1/ (1+k)1 + D1/(1+k)2+ D1/(1+k)3+ D1/(1+k)4+....+D1/(1+k)∞
P0 = D1/k

Onde:
P0= Valor corrente da ação ou valor estimado ou valor teórico ou ainda valor intrínseco da ação.
D1= valor perpétuo dos dividendos.
Ks = taxa de retorno esperada (exigida) da ação pelo investidor.

Exemplos

1) O retorno esperado de determinada ação é de 20%. O último dividendo pago pela empresa foi de $2,5 por ação. Suponhamos que a empresa deverá manter a política de pagar para sempre (prazo indefinido) dividendos de $2,5 por ação, calcule o preço corrente dessa ação.

Resolução

2) Vamos empregar o modelo para calcular o valor de um imóvel. Admita que um imóvel esteja rendendo R$1.450,00 de aluguel mensalmente. Sendo de 1% a.m. o custo de oportunidade de mercado (ganho da melhor alternativa de aplicação disponível) estimar o valor desse imóvel hoje.

Resolução

3) Vamos empregar o modelo para estimar o valor de uma empresa. Admita uma empresa que apresenta um fluxo de caixa livre para a empresa (FCLE) de $100,00/ano perpetuamente. Supondo uma taxa de desconto de 15% ao ano, qual o valor dos ativos operacionais da empresa tomando por base o FCLE?

Resolução


Resolução 1
Nesse exemplo dispomos:
ks = 20%; D1= $2,5
Precisamos calcular: P0 = $?
P0 = $2,5/0,20
P0 = $12,5 por ação



Resolução 2
Nesse exemplo dispomos:
k = 1,0%; Aluguel1= $1.450
Precisamos operar o valor do imóvel0 = $?
Valor do Imovel0 = $1.450/0,01
P0 = $145.000,00 (valor estimado para o imóvel hoje)


Resolução 3
Nesse exemplo dispomos:
k = 15%; FC1= $100
Precisamos operar o valor dos ativos operacionais da empresa empresa0 = $?
Valor dos ativos operacionais da empresa0 = $100/0,15
Valor dos ativos operacionais da empresa0 = $666,67.

Tela 8
Módulo 01 – Conceito de Custo de Capital

4) A JJ S/A é uma empresa madura do setor de componentes para máquinas operadoras. O dividendo mais recente pago aos acionistas ordinários foi de $2,40 por ação. Por causa de sua maturidade e da estabilidade de suas vendas e lucros, a administração da empresa entende que os dividendos permanecerão no nível atual no futuro.

a) Sendo o retorno exigido de 15%, qual é o valor da ação da JJ?
b) Se o risco percebido pelos participantes do mercado aumentar repentinamente, fazendo com que o retorno exigido suba para 17,25%, qual será o valor da ação ordinária hoje?

Resolução

5) Admita que seja prevista uma distribuição anual de dividendos de $0,50 por ação indefinidamente. Determinar o valor dessa ação hoje se os acionistas definirem em 20% a taxa mínima exigida de rentabilidade.

Resolução


Resolução 4

a) Nesse exemplo dispomos:
ks =15%; D0 = D1 = $2,40
Precisamos operar P0 = $?
P0 = $2,40/0,15
P0 = $16,0 por ação.

b) Nesse caso temos: ks =17,25%; D0 = D1 = $2,40;
Precisamos encontrar P0 = $?
P0 = $2,40/0,1725
P0 = $13,91 por ação.


Resolução 5
Nesse exemplo temos: ks =20%; D0 = D1 = $0,50
Precisamos encontrar P0 = $?
P0 = $0,50/0,20
P0 = $2,50 por ação.


Tela 9
Módulo 01 – Conceito de Custo de Capital

4 - Modelo de crescimento constante – modelo de Gordon

No modelo de crescimento nulo dos dividendos observamos que o valor dos dividendos será sempre o mesmo. Agora suponha que a empresa hipotética informe que sobre o valor de $1,0 do último dividendo, D0, irá incidir uma taxa de crescimento anual de 5% para sempre, ou seja, uma taxa de crescimento constante, g.

Lembre-se do modelo anterior, no qual observamos que: D0=D1=D2=D3=......D∞

Agora, diante da nova situação como seria o valor dos dividendos futuros?


D1= D0 (1 + g)1
D2= D0 (1 + g)2
D3= D0 (1 + g)3
D4= D0 (1 + g)4
. .
. .
. .
Dt= D0 (1 + g)t

Segundo Ross, Westerfield e Jordan (2000) se o dividendo cresce a uma taxa constante, então substituímos o problema de prever um número infinito de dividendos futuros pelo problema de prever uma única taxa de crescimento, o que é uma simplificação considerável. Nesse caso, se D0 é o último dividendo pago e g a taxa de crescimento constante, o valor da ação pode ser expresso por:


P0 = D1/(1 + k)1 + D2/(1 + k)2 + D3/(1 + k)3 + ......
P0 = D0(1 + g)1/(1 + k)1 + D0(1 + g)2/(1 + k)2 + D0(1 + g)3/(1 + k)3 + …

Tela 10
Módulo 01 – Conceito de Custo de Capital

Enquanto a taxa de crescimento g for menor do que a taxa de desconto, ks, o valor presente dessa série de fluxos de caixa poderá ser expresso por:


P0 = D0(1 + g)/(ks – g)
P0 = D1/(ks– g)

Onde:
P0 = Valor corrente da ação ou valor estimado ou valor teórico ou ainda valor intrínseco da ação
D1= dividendo projetado para o final do primeiro período
Ks= taxa de retorno mínimo aceitável, ou requerido, ou exigido, sobre a ação, considerando tanto seu risco quanto os retornos disponíveis sobre outros investimentos.
g = taxa de crescimento constante (perpétuo) dos dividendos

Segundo Gitman (2004) esse é o modelo de avaliação com crescimento constante, também conhecido como modelo de Gordon.

A hipótese implícita do modelo é a de que a taxa de crescimento, g, seja inferior à taxa de retorno mínima aceitável (taxa de desconto), ks. Efetivamente, à medida que g for se aproximando de ks, o valor da ação vai convergindo ao infinito.

Partindo-se da equação do valor de uma ação com crescimento constante, obtemos a seguinte equação para o cálculo do custo da ação ordinária:


P0 = D1/( ks– g)
P0 /(ks– g) = D1
ks– g = D1/P0
ks = (D1/P0) + g

Tela 11
Módulo 01 – Conceito de Custo de Capital

Segundo Damodaran (2007) embora o modelo de Gordon seja uma abordagem simples e poderosa para avaliar ações, o seu uso é limitado a empresas com taxa de crescimento estável. Vale ter em mente duas percepções ao estimar uma taxa de crescimento estável.

Primeiro, como a taxa de crescimento dos dividendos de uma empresa tem a expectativa de durar para sempre, pode-se esperar que os seus outros indicadores operacionais (incluindo receitas e lucros) cresçam à mesma taxa. A segunda questão refere-se a qual taxa de crescimento é razoável como uma taxa de crescimento estável. Essa taxa de crescimento deve ser inferior ou igual à taxa de crescimento da economia em que a empresa atua.

Em resumo, o modelo de Gordon é mais adequado a empresas com taxa de crescimento comparável ou inferior à da economia e que possuam políticas bem estabelecidas de pagamento de dividendos, que pretendam manter no futuro. O pagamento de dividendos deve ser consistente com a premissa de estabilidade, já que empresas estáveis geralmente pagam dividendos substanciais. Esse modelo subestimará principalmente o valor de ações de empresas que pagam consistentemente menos dividendos do que podem e acumulam caixa nesse processo.

Tela 12
Módulo 01 – Conceito de Custo de Capital

Exemplos

1) É esperado que no fim do Ano 1 a Empresa Alpha pague um dividendo por ação de $0,50. É esperado um crescimento de dividendos a uma taxa constante de 4,5% ao ano para sempre. A taxa de retorno requerida sobre a ação, ks, é de 15%. Qual é o valor de cada ação da empresa?

Resolução

2) Atualmente, a ação da Empresa Gama é vendida por $20. Cada ação pagou um dividendo de $1,0. É esperada uma taxa de crescimento de dividendos constante de 5,25% ao ano para sempre. Qual é o retorno requerido sobre a ação da empresa? Qual é o preço da ação esperado para daqui a 1 ano? Para daqui a 5 anos? Para daqui a 20 anos?

Resolução

3) Uma ação é negociada a $79 cada. Espera-se obter no fim do ano um dividendo por ação de $10,15, a uma taxa de crescimento constante, g, ao longo do tempo (para sempre). A taxa de retorno requerida da ação é de 17,85%. Se você for um analista que acredita nos mercados eficientes, qual seria sua previsão de g?

Resolução

4) No início de 2008, o preço da ação da Empresa Alpha S.A. era de $100,0. Seus dividendos, em 2007, tinham sido de $12,0 por ação. Os analistas esperam que os dividendos, no futuro, cresçam à taxa constante de 4% ao ano para sempre. Com base no modelo de avaliação de crescimento constante - modelo de Gordon - um investidor médio, que comprou ações ordinárias da Empresa Alpha, ao preço de $100,0, espera uma taxa de retorno anual de quanto?

Resolução


Resolução 1

Nesse exemplo temos fornecido: D1= $0,50; g = 4,5%; ks =15%. O exemplo pede o cálculo de P0 =?
P0 = D1/(ks– g)
P0 = $0,50/(0,15 – 0,045)
P0 = $4,76 por ação


Resolução 2

Nós temos fornecido: D0= $1,0; g = 5,25%; P0 =$20. O exemplo pede inicialmente ks=%. Logo em seguida ele pede P1=$, depois ele pede P5 =$ e, por fim, ele pede P20 =$.
ks = (D1/ P0) + g ou
ks = [D0(1+g)/P0] +g
ks = [$1,0 (1+0,0525)/$20] +0,0525
ks = 0,105125 x 100
ks = 10,5125%

Calcular o preço da ação para daqui a 1 ano
P1 = D0(1+g)2/(ks –g)
P1 = $1,0 (1 + 0,0525)2/(0,105125 – 0,0525)
P1 = $21,05

Outra maneira de operar o valor de P1 seria:
P1 =$20 (1 + 0,0525)
P1 = $21,05

Calcular o preço da ação para daqui a 5 anos
P5 = D0(1+g)6/(ks –g)
P5 = $1,0 (1 + 0,0525)6/(0,105125 – 0,0525)
P5 = $25,8309583

Outra maneira de operar o valor de P5 seria:
P5 =$20 (1 + 0,0525)5
P5 = $25,8309583

Calcular o preço da ação para daqui a 20 anos
P20 = D0(1+g)21/(ks–g)
P20= $1,0 (1 + 0,0525)21/(0,105125 – 0,0525)
P20= $2,928627895/0,052625
P20 = $55,650886

Outra maneira de operar o valor de P20 seria:
P20 =$20 (1 + 0,0525)20
P20= $55,650886


Resolução 3

Nesse exemplo temos: D1 = $10,15; P0=$79; ks=17,85%; precisamos apurar g.
P0= D1/(ks–g)
$79 = $10,15/(0,1785 – g)
$79 (0,1785 – g) = $10,15
0,1785 – g = $10,15/$79
0,1785 – g = 0,128481013
0,1785 – 0,128481013 = g
g = 0,050018987 x 100
g = 5,0018987%

Outra maneira de operar esse exemplo seria:
ks = [(D1/ P0) + g] x 100
0,1785 = ($10,15/$79) + g
0,1785 = (0,128481013 + g)
0,1785 – 0,128481013 = g
g = 0,050018987 x 100
g = 5,0018987%


Resolução 4

Nesse exemplo nós temos: D0 = $12; P0=$100; g=4%; precisamos apurar ks=%?.
ks = (D1/ P0) + g ou
ks = [D0(1+g)/P0] +g
ks = [$12,0 (1 + 0,04)/$100,0] + 0,04
ks = ($12,48/$100) + 0,04
ks = 0,1248 + 0,04
ks = 0,1648 x 100
ks = 16,48%


Tela 13
Módulo 01 – Conceito de Custo de Capital

5) Você é um investidor e deseja calcular o retorno da ação ordinária da Empresa Alpha S/A. A ação, atualmente, está sendo vendida por $90,00 cada. Os analistas esperam que, no futuro, os dividendos cresçam a uma taxa constante, para tanto, estão tomando por base a taxa de crescimento verificada nos últimos cinco anos, conforme demonstrado a seguir:

Ano
Dividendo
2007
$9,10
2006
$8,70
2005
$8,20
2004
$7,70
2003
$7,18

Com base no modelo de Gordon, calcule a taxa de retorno exigida para a ação ordinária da Empresa Alpha S/A.

Resolução

6) Suponha que a Empresa Alpha S/A, uma grande empresa do setor siderúrgico, pagou no último ano dividendo de $3,2 por ação. O preço corrente da ação de Alfa é de $58 por ação. Você estima que o dividendo cresça a uma taxa constante de 6,5% indefinidamente. Qual é o custo da ação ordinária da Empresa Alpha S/A?

Resolução

7) (Brigham, Ehrhardt (2006, p. 411). Você está considerando um investimento em ações ordinárias da KC. Espera-se que a ação pague um dividendo por ação de $2 no fim do ano. O beta da ação é igual a 0,9. A taxa livre de risco é de 5,6% e o prêmio pelo risco de mercado 6,0%. É esperado que a ação tenha um crescimento de dividendo a uma taxa constante g. Atualmente, a ação é vendida a $25 cada. Supondo que o mercado esteja em equilíbrio, que preço o mercado aposta que a ação terá no final de três anos? Isto é, qual é o P3?

Resolução


Resolução 5

Nesse exercício, você deverá de imediato calcular o valor da taxa de crescimento histórica dos dividendos. Somente de posse de “g” é que você poderá avançar no exercício. Na verdade, você já possui duas informações importantes, a saber:

• P0 = $90,0 (preço corrente da ação, não esqueça: atualmente está sendo vendida);
• D0 = $9,10, nesse exercício, o ano de 2007 é o último ano, logo, D1 deverá ser calculado partindo-se de 2007.

Como calcular o valor de g?
g = [(último dividendo pago/primeiro dividendo pago)1/(n-1) -1] x100
g = [($9,10/$7,18)1/4 –1] x 100
g = 6,1033844% ao ano

Resolução pela HP 12 C
9.10 enter 7.18 ÷ 1 enter 4 ÷ yx 1 - 100 x
No visor da máquina teremos 6,1033844

De posse de g, podemos calcular D1
D1 = $9,10 (1 + 6,1033844/100)
D1 = $9,10 (1 + 0,061033844)
D1 = $9,10 x 1,061033844
D1 = $9,65540798

Resolução pela HP 12 C
9.10 enter 1 enter 6.1033844 enter 100 ÷ + x
No visor da máquina teremos 9,65540798

Agora vamos para o custo da ação ordinária:
ks = [($9,65540798/$90,0) + 0,061033844] x 100
ks = 16,83161549%

Resolução pela HP 12 C
9.65540798 enter 90 ÷ 0,061033844 + 100 x
No visor da máquina teremos 16,83161549

Se você tem facilidade com a HP 12 C poderá fazer o cálculo direto, observe:
9,10 enter 9.10 enter 7.18 ÷ 1 enter 4 ÷ yx x 90 ÷ 9.10 enter 7.18 ÷ 1 enter 4 ÷ yx 1 - + 100 x
No visor da máquina teremos 16,83161549



Resolução 6

Identificando as variáveis:

a) dividendo pago: observe que temos uma informação no passado (pagou no último ano), isto é, já aconteceu, logo, estamos diante de D0 e não de D1. Por quê? Seria D1 se viesse, por exemplo: a Empresa Alpha espera pagar no final do próximo ano. Não é isto que estamos lendo no exercício. Portanto, teremos que calcular o valor de D1. Como fazer isto?

D1 = D0 (1 + g)
D1 = $3,2 (1 + 6,5/100)
D1 = $3,2 (1 + 0,065)
D1 = $3,2 x 1,065
D1 = $3,408

b) valor corrente da ação, P0 = $58,0 por ação;

c) taxa de crescimento constante, g = 6,5% ou 0,065;
Portanto, o custo da ação ordinária da Empresa Alfa S/A será:
ks = ($3,408/$58,0) + 0,065
ks = 0,1237586207 x 100
ks = 12,37586207%

Observe, você poderia resolver este exercício direto, isto é, sabendo que está diante de D0é só aplicar a fórmula partindo de D0, veja:
ks = [($3,2 x 1,065)/$58] + 0,065
ks = 0,1237586207 x 100
ks = 12,37586207%

Resolução pela HP 12 C
3.2 enter 1 enter 6.5 enter 100 ÷ + x 58 ÷ 0.065 + 100 x
No visor da máquina teremos 12,37586207


Resolução 7

Nesse exemplo, primeiro devemos operar a taxa de corte, taxa de desconto. O exemplo deixa implícito que a taxa de corte deverá ser operada por meio do CAPM (Modelo de Precificação de Ativos de Capital).
Kj = RF + [ßj (KM– RF)]
Ki = ? (taxa de corte)
RF = 5,6%
ßj = 0,9 (risco sistemático defensivo)
PRM = KM– RF
PRM = 6%
Ki = 5,6 + (0,9 x 6)
Ki = 11% taxa de desconto do exemplo

Agora, vamos operar a taxa de crescimento constante dos dividendos.
g = Ks –(D1/P0)
g = %?
Ks = 11%
D1= $2,0
P0 = $25
g = 0,11 – ($2,0/$25)
g = 0,11 – 0,08
g = 0,03 x 100
g = 3%

De posse da taxa de crescimento constante dos dividendos, será possível estimar o preço da ação para o período 3 (Ano 3).
P3 = D0(1 + g)4/(ks– g)
P3 = $1,941747573(1 + 0,03)4/(0,11 - 0,03)
P3 = $2,185454/0,08
P3 = $27,318175 ou 27,32

Outra maneira de chegar ao valor estimado para a ação seria:
P3 = P0 (1 +g)3
P3 = $25 (1+0,03)3
P3 = $27,318175 ou $27,32

Tela 14
Módulo 01 – Conceito de Custo de Capital

5 - Modelo de crescimento variável

Segundo Gitman (2004) os modelos de crescimento nulo e constante não permitem que ocorra variação nas taxas de crescimento esperadas. Como elas poderiam subir ou cair por causa de mudanças de expectativas, é útil considerar um modelo de crescimento variável que permita alterações na taxa de crescimento dos dividendos.

Segundo Damodaran (2007) o modelo de crescimento variável pode ser operado de três maneiras:

a) o modelo de desconto de dividendos em dois estágios;
b) o modelo H de avaliação de crescimento;
c) modelo de desconto de dividendos em três estágios.

No nosso estudo, iremos operar basicamente o modelo em dois estágios. Outro detalhe, os nossos exemplos estarão voltados basicamente para apurar o valor (preço) corrente da ação, P0, e não o custo da ação, ks, ou seja, vamos treinar, de forma muito simples, avaliação de ações utilizando o modelo de crescimento variável.

Tela 15
Módulo 01 – Conceito de Custo de Capital

Exemplos

1) A WP paga um dividendo por ação de $1,50. É esperado um crescimento de dividendos de 10% ao ano nos próximos três anos e de 4% daí em diante. Qual é o dividendo por ação esperado para cada um dos próximos 4 anos?

Resolução

2) Uma empresa encontra-se em fase de grande expansão, com o lançamento de novos produtos no mercado. Os dividendos atuais são de 1,15/ação e espera-se um crescimento de 10% ao ano nos próximos cinco anos. Após esse período de forte rendimento, espera-se que a taxa de crescimento se estabilize em 6% ao ano. Determinar o valor da ação hoje, sendo de 16% ao ano a taxa de retorno exigida pelos investidores.

Resolução

3) A Empresa Beta S/A espera pagar os seguintes dividendos nos próximos quatro anos: $12, $10, $6 e $2. A partir de então, a empresa promete manter uma taxa constante de crescimento de 6% em seus dividendos, para sempre. Se a taxa exigida de retorno da ação é 16%, qual é o preço da ação hoje?

Resolução

4) Uma empresa paga atualmente um dividendo por ação de $2,0. É esperado que o dividendo da empresa cresça a uma taxa de 20% ao ano nos próximos dois anos; daí por diante o dividendo crescerá a uma taxa constante de 7%. A ação da empresa tem beta igual a 1,2, a taxa livre de risco é de 7,5% e o prêmio pelo risco de mercado é de 4%. Qual seria sua estimativa para o preço corrente da ação?

Resolução


Resolução 1

Nesse exemplo nós temos que D0 = $1,50, portanto, será necessário aplicar as taxas de crescimento para cada um dos próximos cinco anos, assim:
D1 = D0 (1 + g)
D1 = $1,50 (1 + 0,10)
D1 = $1,65

O cálculo poderia ser feito dessa maneira:
$ 1,50 x (10/100) = $0,15
$ 1,50 + $0,15 = $1,65
D2 = D0 (1 + g)2
D2 = $1,50 (1 + 0,10)2
D2 = $1,815

O cálculo poderia ser feito dessa maneira:
$1,65 x 0,10 = 0,165
$1,65 + $0,165 = $1,815
D3 = D0 (1 + g)3
D3 = $1,50 (1+0,10)3
D3 = $1,9965

O cálculo poderia ser operado dessa maneira:
$1,815 x 0,10 = $0,1815
$1,815 + $0,1815 = $1,9965
D4 = D3 (1 + g)1
D4 = $1,9965 (1 + 0,04)
D4 = $2,07636

O cálculo poderia ser operado assim:
$1,9965 x 0,04 =$0,07986
$1,9965 + $0,07986 = $2,07636
D5 = D3 (1 + g)2
D5 = $1,9965 (1+ 0,04)2
D5 = $2,1594144

O cálculo poderia ser realizado assim:
$2,07636 x 0,04 = $0,0830544
$2,07636 + $0,0830544 = $2,1594144


Resolução 3

Nesse exemplo dispomos:
D1 = $12; D2 = $10; D3 = $6; D4 = $2
D5 = D4 (1,0 + 0,06)
D5 = $2 (1,06)
D5 = $2,12

Primeiro vamos calcular o valor presente dos quatro primeiros dividendos (período de crescimento decrescente):
P0 = $12/1,161 + $10/1,162+ $6/1,163 + $2/1,164
P0 = $22,72498484

Agora vamos calcular o valor presente para a fase de crescimento constante:
P4 = D5/(ks– g)
P4 = $2,12/(0,16 – 0,06)
P4 = $21,20
P0 = $21,20/1,164
P0 = $11,70857128

Somando os dois valores encontrados:
P0 = $22,72498484 + $11,70857128
P0 = $34,43 por ação


Resolução 4

a) Nesse exemplo primeiro iremos operar o custo da ação ordinária, para tanto o mesmo será calculado com base no CAPM, portanto:
Kj = RF + [ßj (KM – RF)]
Ki = ? (taxa de corte)
RF = 7,5%
ßj = 1,2 (risco sistemático mais volátil)
PRM = KM– RF
PRM = 4%
Ki = 7,5 + (1,2 x 4)
Ki = 12,30% taxa de desconto do exemplo

Vamos agora identificar as outras variáveis do exemplo:
D0 = $2,0
g1 = 20%
ks= 12,30%
t = 2
g2= 7%
DN+1 = $3,08 (será operado no desenvolvimento do exemplo)
N = 2

b) P0 = [∑D0 x (1 + g1)t/(1 +ks)t]
Os dividendos atuais: D0 = $2,0/ação

Dividendos com crescimento de 20% ao ano
D1 = $2,0 x (1,20)1 = $2,40
D2 = $2,0 x (1,20)2 = $2,88

O valor presente dos dividendos esperados nos dois primeiros anos atinge o seguinte valor:
P0 = $2,4/1,12301 + $2,88/1,12302
P0 = $ 4,42

c) P0 = [1/(1+ks)N x DN+1/(ks –g2)]
D3 = $2,88 (1 + 0,07)
D3 = $3,08
P0 = 1/(1 + 0,1230)2 x $3,08/(0,1230 – 0,07)
P0 = 0,792940294 x 58,11320755
P0 = $46,08

O item c poderia ser operado também da seguinte maneira:
P0 = [$3,0816/(0,1230 – 0,07)]/(1 + 0,1230)2
P0 = $46,08

d) P0 = [∑D0 x (1 + g1)t/(1 +ks)t]+ [1/(1+ks)N x DN+1/(ks–g2)]
P0 = $4,42 + $46,08
P0 = $50,50 por ação.

Tela 16
Unidade 01 - Matemática Básica

Resolução 2

Esse exemplo poderá ser operado com base na seguinte equação extraída de Gitman (2004, p. 280)


Onde:

P0 = Valor corrente da ação ou valor estimado ou valor teórico ou ainda valor intrínseco da ação
D0 = dividendo atual
DN+1= dividendo do primeiro período de crescimento constante
t = período de taxa de inicial
g1= taxa de crescimento inicial
ks= taxa de desconto = custo da ação ordinária = taxa de retorno exigida pelo investidor = taxa de corte
N = período de crescimento constante (perpétuo)
g2= taxa de crescimento constante (perpétuo)

Nesse exemplo temos:

ks= 16%
D0 = $1,15
T = 5
g1= 10%
g2= 6%
N = 5
DN+1 = $1,96321169 (será apurado no desenvolvimento do exemplo)

a) P0 = [∑D0 x (1 + g1)t/(1 +ks)t]

Os dividendos atuais: D0 = $1,15/ação
Dividendos com crescimento de 10% ao ano
D1 = $1,15 x (1,10)1 = $1,265
D2 = $1,15 x (1,10)2 = $1,3915
D3 = $1,15 x (1,10)3 = $1,53065
D4 = $1,15 x (1,10)4 = $1,683715
D5 = $1,15 x (1,10)5 = $1,8520865

O valor presente dos dividendos esperados nos cinco primeiros anos atinge o seguinte valor:

P0 = $1,265/1,161 + $1,3915/1,162 + $1,53065/1,163 +1,683715/1,164 + $1,8520865/1,165
P0 = $ 4,91695438

b) P0 = [1/(1+ks)N x DN+1/(ks–g2)]

Os dividendos que se iniciam no ano 6 atingem a:
D6 = $1,8520865 x (1,06)1 = $1,96321169
D7 = $1,8520865 x (1,06)2 = $2,081004391
D8 = $1,8520865 x (1,06)3 = $2,205864655
E assim por diante.

O valor presente desses dividendos é obtido no ano 5. Para transferir esse valor para o ano 0 (momento atual), deve-se atualizá-lo pelo fator: (1,16)5, ou seja:

P0 = [$1,96321169/(0,16 – 0,06)]/(1,16)5
P0 = $19,6321169/2,100341658
P0 = $9,347106374

Vamos agora operar a segunda parte da equação pela fórmula:

P0 = 1/(1+0,16)5 x $1,96321169/(0,16 – 0,06)
P0 = 0,476113015 x $19,6321169
P0 = $9,347106374

Logo, o valor presente do total dos dividendos no momento 0, que representa o valor teórico da ação, atinge a:

c) P0 = [SD0 x (1 + g1)t/(1 +ks)t]+ [1/(1+ks)N x DN+1/(ks–g2)]

P0 = $ 4,91695438 + $9,347106374
P0 = $14,26406075 por ação


Tela 17
Módulo 01 – Conceito de Custo de Capital

5) Suponha que a média do setor de sua empresa tenha uma taxa de crescimento esperada de 6% e que seus rendimentos de dividendos sejam de 7%. Sua empresa é quase tão arriscada quanto à média do setor, mas terminou com muito sucesso um trabalho de P&D que o leva a acreditar que seus lucros e dividendos crescerão a uma taxa de 50% em 2009 e de 25% no ano seguinte, após o que o crescimento deve ser igual à taxa média do setor, de 6%. O último dividendo pago foi de $1,0 por ação. Qual o valor por ação de sua empresa?

Resolução

6) A NM está analisando a compra à vista das ações da GT. Durante o ano que acaba de se encerrar, a GT obteve lucro de $4,25 por ação (LPA) e pagou dividendos de $2,55 por ação, em dinheiro. Espera-se que os lucros e dividendos da GT cresçam 25% ano nos próximos três anos e, depois disso, 10% ao ano para sempre. Qual é o preço máximo por ação que a NM deveria pagar pela GT, caso haja um retorno exigido de 15% em investimentos com características de risco semelhante?

Damodaran (2007, p. 109) apresenta a fórmula para o modelo de desconto de dividendos em dois estágios. Para o nosso exemplo vamos fazer uma adaptação entre essa fórmula e a fórmula já apresentada do professor Gitman.

P0 = {D0 x(1 + g1) x [1 – (1+g1)t/(1+ Ks)t]}/(Ks –g1) + [1/(1+ks)N x DN+1/(ks –g2)]

Resolução

7) A HP Hotéis está iniciando um projeto de remodelação e expansão que durará três anos. A atividade de construção limitará os lucros durante esse período, mas, quando estiver concluída, deverá permitir à empresa que cresça muito mais rapidamente em termos de lucros e dividendos. No ano passado, a empresa pagou um dividendo de $3,40 por ação. Ela espera crescimento nulo no próximo ano. Nos anos 2 e 3 deve haver crescimento de 5% e, no ano 4, de 15%; do ano 5 em diante o crescimento deverá ser constante igual a 10% ao ano. Qual é o preço máximo que um investidor que exige um retorno de 14% deveria pagar por ação ordinária da HP Hotéis?

Resolução


Resolução 5

Nesse exemplo dispomos:
D0 = $1,0 (dividendo pago em 2008)
Ks = 6% + 7% = 13%
g1 = 50%
g2 = 25%
gN= 6% (taxa de crescimento constante)

Nesse exemplo iremos calcular o valor dos dividendos para D1 e D2, logo, a seguir iremos calcular o valor dos dividendos para DN+1.
D1 = $1,0 (1+0,50)
D1 = $1,50
D2 = $1,50 (1+0,25)
D2 = $1,875
D3 = $1,875(1+0,06)
D3 = $1,9875 = DN+1
P0 = ($1,50/1,13) + ($1,875/1,132 + [$1,9875/ (0,13 – 0,06) /1,132]
P0 = $1,327433628 + $1,468400031 + ($28,39285714/1,2769)
P0 = $2,795833938 + $22,2357719
P0 = $25,03160584 ou $25,03 por ação


Resolução 6

Nesse exemplo dispomos:
D0 = $2,55
Ks = 15% (custo de oportunidade)
g1 = 25% (fase de crescimento acelerado)
g2 = 10% (fase de crescimento constante, perpétuo).
DN+1 = D3 (a ser calculado)
t = 3 (fase de crescimento acelerado)
N = 3 (período considerado para o cálculo do valor presente dos dividendos durante o período de crescimento constante. De posse de D4, nós estaremos em condições de calcular P3).

Cálculos:
D1 = $2,55 (1 + 0,25)1
D1 = $3,1875
D2 = $2,55 (1+ 0,25)2
D2 = $3,984375
D3 = $2,55 (1 + 0,25)3
D3 = $4,98046875
D4 = DN+1 = $ 4,98046875(1+ 0,10)
D4 = DN+1 = $5,478515625 (cuidado, não esqueça que a partir do período quatro a taxa de crescimento dos dividendos será constante, portanto, o valor de D4 terá que ser operado considerando taxa de crescimento de 10% e não 25%).

P0 = {$2,55 x (1+0,25) x [1 – (1 +0,25)3/(1+0,15)3]}/(0,15 – 0,25) + [1/(1+0,15)3 x $5,478515625/(0,15 – 0,10)]
P0 = {$3,1875 x [1 – 1,953125/1,520875]}/-0,10 + [1/1,520875 x $5,478515625/0,05]
P0 = [$3,1875 x (1 – 1,284211391)]/-0,10 + (0,657516232 x $109,5703125)
P0 = ($3,1875 x -0,284211391)/-0,10 + $72,04425906
P0 = (-$0,905923809/-0,10) + $72,04425906
P0 = $9,059238088 + $72,04425906
P0 = $81,10349715 ou $81,10 por ação (preço máximo por ação que a NM deveria pagar pela GT).


Resolução 7

Nesse exemplo dispomos:
D0 = $3,40
Ks = 14%
g1 = 5%
g2 = 15%
gN = 10% (taxa de crescimento constante)

Vamos aos cálculos:
D1 = $3,40 (1 + 0)1
D1 = $3,40 (crescimento nulo dos dividendos, ou seja, os dividendos serão idênticos ao dividendo atual).
D2 = $3,40 (1+0,05)2
D2 = $3,7485
D3 = $3,40 (1+0,05)3
D3 = $3,935925
D4 = $3,935925 (1 + 0,15)
D4 = $4,52631375
D5 = $4,52631375 (1 + 0,10)
D5 = $4,978945125

Cálculo do preço da ação:
P0 = [($3,40/1,141) + ($3,7485/1,142) + ($3,935925/1,143) + ($4,52631375/1,144)] + [$4,978945125/(0,14 – 0,10)]/1,144
P0 = ($2,98245614 + $2,884349030 + $2,656637265 + $2,679941101) + ($124,4736281/1,688960160)
P0 = $11,20338354 + $73,69838025
P0 = $84,90176379 ou $84,90 por ação (preço máximo que poderia ser pago por cada ação da HP Hotéis).

Tela 18
Módulo 01 – Conceito de Custo de Capital

8) O dividendo anual mais recente da LI foi de $1,80 por ação e o retorno exigido da empresa é igual a 11%. Encontre o valor de mercado da ação da LI quando:

a) O crescimento esperado dos dividendos é de 8% ao ano, por três anos, seguido de um crescimento anual constante de 5% do ano 4 para sempre.

Resolução

b) O crescimento esperado dos dividendos é de 8% ao ano, por três anos, seguido de um crescimento anual constante de 0% do ano 4 para sempre.

Resolução

c) O crescimento esperado dos dividendos é de 8% ao ano, por três anos, seguindo de um crescimento anual constante de 10% do ano 4 para sempre.

Resolução

9) A JJ S/A está se expandindo rapidamente e atualmente necessita reter todos os seus lucros (índice de payout=0, isto é, índice de retenção=1,0), por isso, ela não distribui lucros. Porém, os investidores esperam que a JJ comece a pagá-los com o primeiro dividendo de $1,0 para daqui a três anos. O dividendo deve crescer rapidamente, a uma taxa de 50% ao ano, durante os Anos 4 e 5. Após o Ano 5, a empresa deverá crescer a uma taxa constante de 8% por ano. Se a taxa de retorno requerida sobre a ação for de 15%, qual o valor da ação hoje?

Resolução

10) Assumimos que a Empresa Alpha, uma das principais do seu setor de atuação, irá manter vantagem competitiva da sua marca pelos próximos cinco anos. Durante esse período (fase de crescimento alto) o crescimento dos dividendos será de 16%; a partir do sexto ano a empresa irá experimentar crescimento constante (perpétuo) nos dividendos de 3,5% ao ano. Durante a fase de crescimento acelerado, o custo de capital próprio da empresa foi estimado em 15%, caindo para 13,5% durante a fase de crescimento perpétuo. O dividendo pago no último exercício social foi de $2,0 por ação. Com base no modelo de crescimento variável, estimar o preço corrente da ação da Empresa Alfa.

Resolução


Resolução a

Nesse exemplo dispomos:
D0 = $1,80
Ks = 11% (custo de oportunidade)
g1 = 8% (fase de crescimento acelerado)
g2 = 5% (fase de crescimento constante, perpétuo).
DN+1 = D4 (a ser calculado)
t = 3 (fase de crescimento acelerado)
N = 3 (período considerado para o cálculo do valor presente dos dividendos durante o período de crescimento constante. De posse de D4, nós estaremos em condições de calcular P3).

Cálculos:
D1 = $1,80 (1 + 0,08)1
D1 = $1,944
D2 = $ 1,80(1+0,08)2
D2 = $ 2,09952
D3 = $ 1,80(1 +0,08)3
D3 = $ 2,2674816
D4 = DN+1 = $2,2674816 (1+0,05)
D4 = DN+1 = $2,38085568 (cuidado, não esqueça que a partir do período quatro a taxa de crescimento dos dividendos será constante, portanto, o valor de D4 terá que ser operado considerando taxa de crescimento de 5% e não 8%).

P0 = {$1,80 x (1+0,08) x [1 – (1 +0,08)3/(1+0,11)3]}/(0,11 –0,08 ) + [1/(1+0,11)3 x $2,38085568 /(0,11 –0,05 )]
P0 = {$1,9440 x [1 –1,259712/1,3676310]}/0,03 + [1/1,3676310 x $2,38085568/0,06]
P0 = [$1,9440 x (1 –0,921090557)]/0,03 + (0,731191381 x $39,680928)
P0 = ($1,9440 x 0,07890943)/0,03 + $29,01435254
P0 = ($0,153399932/0,03) + $29,01435254
P0 = $5,113331063 + $29,01435254
P0 = $34,12768360 ou $34,13 por ação


Resolução b

Nesse exemplo dispomos:
D0 = $1,80
KS = 11% (custo de oportunidade)
g1 = 8% (fase de crescimento acelerado)
g2 = 0% (fase de crescimento constante, perpétuo).
DN+1 = D4 (a ser calculado)
t = 3 (fase de crescimento acelerado)
N = 3 (período considerado para o cálculo do valor presente dos dividendos durante o período de crescimento constante. De posse de D4, nós estaremos em condições de calcular P3).

Cálculos:
D1 = $1,80 (1 + 0,08)1
D1 = $1,944
D2 = $ 1,80(1+0,08 )2
D2 = $ 2,09952
D3 = $ 1,80(1 +0,08 )3
D3 = $ 2,2674816
D4 = DN+1 = $2,2674816 (1+0)
D4 = DN+1 = $2,2674816

P0 = {$1,80 x (1+0,08) x [1 – (1 +0,08)3/(1+0,11)3]}/(0,11 –0,08 ) + [1/(1+0,11)3 x $2,2674816/(0,11 –0)]
P0 = {$1,9440 x [1 –1,259712/1,3676310/]}/0,03 + [1/1,3676310 x $2,2674816/0,11]
P0 = [$1,9440 x (1–0,921090557)]/0,03 + (0,731191381 x $20,61346909)
P0 = ($1,9440 x 0,07890943)/0,03 + $15,07239093
P0 = ($0,153399932/0,03) + $15,07239093
P0 = $5,113331063 + $15,07239093
P0 = $20,18572199 ou $20,19 por ação


Resolução c

Nesse exemplo dispomos:
D0 = $1,80
Ks = 11% (custo de oportunidade)
g1 = 8% (fase de crescimento nos três primeiros anos)
g2 = 10% (fase de crescimento constante).
DN+1 = D4 (a ser calculado)
t = 3 (fase de crescimento nos três primeiros anos)
N = 3 (período considerado para o cálculo do valor presente dos dividendos durante o período de crescimento constante. De posse de D4, nós estaremos em condições de calcular P3).

Cálculos:
D1 = $1,80 (1 + 0,08)1
D1 = $1,944
D2 = $ 1,80(1+0,08 )2
D2 = $ 2,09952
D3= $ 1,80(1 +0,08 )3
D3 = $ 2,2674816
D4 = DN+1 = $2,2674816 (1+0,10)
D4 = DN+1 = $2,494229760

P0 = {$1,80 x (1+0,08) x [1 – (1 +0,08)3/(1+0,11)3]}/(0,11 –0,08 ) + [1/(1+0,11)3 x $2,494229760/(0,11 –0,10)]
P0 = {$1,9440 x [1 –1,259712/1,3676310/]}/0,03 + [1/1,3676310 x $2,494229760/0,01]
P0 = [$1,9440 x (1–0,921090557)]/0,03 + (0,731191381 x $249,4229760)
P0 = ($1,9440 x 0,07890943) /0,03 + $182,3759303
P0 = ($0,153399932/0,03) + $182,3759303
P0 = $5,113331063 + $182,3759303
P0 = $187,4892614 ou $187,49 por ação

Operando via HP 12C
1.80 enter 1 enter 0.08 + x 1 enter 0.08 + 3 yx 1 enter 0.11 + 3 yx÷ 1 – CHS 0.11 enter 0.08 - ÷ x STO 1
1 enter 1 enter 0.11 + 3 yx÷ 1.80 enter 1 enter 0.08 + 3 yx x 1 enter 0.10 + x 0.11 enter 0.10 - ÷ x RCL 1 +
No visor da máquina você encontra 187,4892622


Resolução 9

Nesse exemplo dispomos:
D3 = $1,0
KS = 15% (taxa de desconto)
g1 = 50% (fase de crescimento acelerado)
g2 = 8% (fase de crescimento constante-perpétuo-)
DN+1 = D6 (a ser calculado)
t = 3 (fase de crescimento acelerado)
N = 5 (período considerado para o cálculo do valor presente dos dividendos durante o período de crescimento constante. De posse de D4, nós estaremos em condições de calcular P5).

Cálculos:
D3 = $1,0 (a empresa irá começar o pagamento dos dividendos a partir do terceiro ano; essa é a expectativa dos investidores).
D4 = $1,0 (1 +0,50)1
D4 = $1,50
D5 = $1,0 (1 +0,50)2
D5 = $2,25
D6 = $2,25 (1 +0,08)1
D6 = $2,43
P0 = [($1,0/1,153) + ($1,50/1,154) + ($2,25/1,155)] + {[$2,43/(0,15 – 0,08)]/1,155
P0 = [($0,657516232 + $0,857629868 +$1,118647655)] + [($2,43/0,07)/2,011357187]
P0 = $2,633793755 + ($34,71428571/2,011357187)
P0 = $2,633793755 + $17,25913524
P0 = $19,892929 ou $19,89 por ação.

Operando via HP 12C
1.0 enter 1.15 enter 3 yx÷ 1.5 enter 1.15 enter 4 yx÷ + 1.0 enter 1.5 enter 2 yx x 1.15 enter 5 yx÷ + STO 1
1.0 enter 1.5 enter 2 yx x 1.08 x 0.15 enter 0.08 - ÷ 1.15 enter 5 yx÷ RCL 1 +
No visor da máquina você encontra 19,89292900


Resolução 10

Nesse exemplo dispomos das seguintes informações:
D0 = $2,0
g1 = 16% (taxa de crescimento dos dividendos no período de alto crescimento)
g2 = 3,5% (taxa de crescimento dos dividendos no período de crescimento estável, para sempre.
Ks,hg = 15% (custo de capital próprio ou taxa de desconto durante o período de alto crescimento)
Ks,st = 13,5% ( custo de capital próprio ou taxa de desconto durante o período de crescimento estável, perpétuo)
DN+1 = D6 (a ser calculado)
t = 5 (fase de crescimento acelerado)
N = 5 (período considerado para o cálculo do valor presente dos dividendos durante o período de crescimento constante. De posse de D6, nós estaremos em condições de calcular P5).
Para esse exemplo vamos operar com a fórmula adaptada de Damodaran (2007, p. 109).

Equação
P0 = {D0 x (1 x g1) x [1 � (1 +g1)t/(1+ Ks,hg)t]}/( Ks,hg� g1) + DN+1/( Ks,st � g2) (1 + Ks,hg)n


Primeiro iremos estimar o valor de DN+1:
DN+1 = D0 (1 + g1)5 x (1 + g2)
DN+1 = $2,0 (1 + 0,16)5 x (1 + 0,035)
DN+1 = $4,347707232 ou $4,35

 Agora vamos estimar o preço corrente da ação:

P0 = {$2,0 x (1 + 0,16) x [1- (1 +0,16)5/(1 + 0,15)5]}/(0,15 – 0,16) + $4,35/(0,135 – 0,035) x (1 + 0,15)5
P0 = [$2,32 x (1 – 1,044241009)/-0,01] + ($4,35/0,201135719)
P0 = $10,26391409 + $21,62718799
P0 = $31,89110208 ou $31,89

Se a ação da Empresa Alpha estiver sendo negociada por um preço menor que $31,89, a ação estará sendo negociada subavaliada, caso contrário, se o preço vigente no mercado for maior que $31,89 a ação estará superavaliada.

Resolução pela HP12C
2.0 enter 1.16 x 1.16 enter 5 yx 1,15 enter 5 yx÷ 1 – CHS x 0.15 enter 0.16 - ÷ STO 1 4.35 enter 0.135 enter 0.035 - 1.15 enter 5 yx x ÷ RCL 1 +
No visor da máquina irá aparecer 31,89110208 ou $31,89

Tela 19
Módulo 01 – Conceito de Custo de Capital

Resumo

Uma empresa, para fazer investimentos, necessita de fontes de dinheiro; essas fontes têm origem no passivo da empresa por meio do passivo exigível e do patrimônio líquido. O dinheiro oriundo do passivo exigível poderá ser de banqueiros ou de investidores. No patrimônio líquido temos dinheiro oriundo dos lucros gerados no negócio e também de ações ordinárias e preferenciais. Para calcular o custo de capital numa empresa se faz necessário apurar o custo individual de cada uma das fontes, assim como o peso de cada uma das fontes.

O custo da ação ordinária poderá ser medido por dois modelos: modelo de crescimento constante (Modelo de Gordon) e modelo de precificação de ativos de capital (CAPM).

Diante de uma situação onde a empresa irá pagar sempre o mesmo dividendo, o valor presente do preço da ação será estimado pelo modelo de crescimento nulo.

Diante de uma situação em que os dividendos irão experimentar taxas de crescimento constante, para sempre, será empregado o modelo de crescimento constante (Modelo de Gordon) tanto para se estimar o preço corrente da ação quanto o custo da ação ordinária da empresa.

Os modelos de crescimento nulo e constante não permitem que ocorram variações nas taxas de crescimento esperadas dos dividendos; como alternativa para esses dois modelos existe o modelo de crescimento variável, que pode ser operado de três maneiras:

a) o modelo de desconto de dividendos em dois estágios;
b) o modelo H de avaliação de crescimento;
c) modelo de desconto de dividendos em três estágios.

Unidade 3 Módulo 2
Tela 20
Módulo 01 – Conceito de Custo de Capital
1 - Custo de emissão de novas ações ordinárias – kn

A Companhia Vale do Rio Doce é uma das maiores empresas de capital privado no Brasil. Em janeiro de 2009 foi considerada a segunda maior mineradora do mundo. A Vale, para tocar os seus negócios, precisa de dinheiro, muitas vezes para crescimento orgânico e outras, para comprar empresas do setor de mineração. No relatório enviado a CVM (Comissão de Valores Mobiliários) referente ao terceiro trimestre de 2008, encontramos:


“Em julho de 2008, a Vale, através de oferta global, emitiu 256.926.766 ações ordinárias e 164.402.799 ações preferenciais registrada no Brasil e no exterior. Dessa forma, a Companhia captou o valor de R$ 18.450 milhões, tendo o capital social aumentado neste valor. Em agosto de 2008, a Vale, através de oferta suplementar, emitiu 24.660.419 ações preferenciais, captando o valor de R$ 984 milhões. Com o fim da operação, o capital social aumentou em R$19.434 milhões e adicionalmente foi registrado em conta retificadora de custo de captação dos recursos, no valor de R$ 161 milhões. Assim, o capital social passou a ser composto de 3.256.724.482 ações ordinárias, e de 2.108.579.618 ações preferenciais, montando a R$ 47.434 milhões”.

A emissão de novas ações ordinárias e preferenciais feita pela Vale foi uma operação de oferta pública de ações, também conhecida por uma operação de underwriting. Nessa operação, nós temos a Vale em busca de dinheiro e os investidores querendo comprar as novas ações da Vale. Ocorre que essa operação não tem como ser feita diretamente entre a Vale e os investidores, fazendo-se necessário a figura de um intermediário no negócio. Quem é esse intermediário? São os bancos de investimento, os bancos múltiplos com carteira de investimento, as corretoras de títulos e valores mobiliários e as distribuidoras de títulos e valores mobiliários. A Vale contratou os serviços desse tipo de intermediários financeiros, para tanto, a Vale pagou uma comissão pelos serviços de colocação dos papéis (ações).



A operação de underwhiting envolve:

• a empresa: que entrega novas ações e recebe dinheiro;
• o investidor: que entrega dinheiro em troca das novas ações;
• a instituição financeira especializada: que recebe uma comissão pelos serviços prestados para a empresa que emite as ações.

Tela 21
Módulo 01 – Conceito de Custo de Capital

A Vale não desembolsou dinheiro somente com a comissão de underwriting. Uma operação de lançamento de novas ações, bem como de emissão de dívida, irá pedir dinheiro para:

• os serviços de escritórios de advocacia,
• publicações em jornais,
• registro nos órgãos reguladores (no Brasil a CVM, nos EUA a SEC),
• registro em bolsas de valores,
• rodadas de reuniões (road show) com analistas de investimento e potenciais investidores.

A lista de gastos não costuma ser pequena.

Descrevemos de forma muito sucinta a emissão primária, ou seja, a parte do negócio envolvendo a empresa emissora e os investidores (aqueles que compraram as ações na fonte), com os intermediários financeiros no comandando da operação.

Depois da operação primária vem o registro das ações em bolsa de valores, ou seja, no mercado secundário. Feito o registro, as novas ações da Vale poderão ser negociadas livremente no mercado, agora entre investidores: compradores e vendedores de ações.


Tela 22
Módulo 01 – Conceito de Custo de Capital

Lemes Júnior, Rigo e Cherobim (2002) afirmam que na subscrição de novas ações, a empresa incorre nos custos de lançamento – emissão, corretagem, deságios – que resultam no custo de capital superior ao das ações existentes.

Segundo Gitman (2004), normalmente, para que uma emissão de novas ações seja efetuada, precisa haver underpricing – venda a um preço inferior a seu preço corrente de mercado, P0. Além do underpricing, devem ser considerados, também, os custos de lançamento, a saber:

• comissão de underwriting,
• gastos com publicações em veículos de comunicação,
• gastos com escritórios de advocacia,
• gastos com a agência reguladora (no caso do Brasil, a CVM) etc.

Tela 23
Módulo 01 – Conceito de Custo de Capital

O underpricing de emissões de novas ações ocorre por diversos motivos. Em primeiro lugar, quando o mercado está em equilíbrio (ou seja, a quantidade demandada de ações é igual à quantidade ofertada), uma demanda por ações adicionais só pode ser gerada com um preço mais baixo.

Em segundo lugar, quando são emitidas novas ações, a participação de cada uma na propriedade da empresa é diluída, o que justifica um valor mais baixo para a ação.

Finalmente, muitos investidores encaram a emissão de novas ações como um sinal de que a administração está recorrendo ao financiamento com ações ordinárias porque acredita que estão supervalorizadas. Ao reconhecerem essa informação, comprarão ações somente a um preço inferior ao valor corrente de mercado. Esses e outros fatores exigem que haja underpricing nos lançamentos de ações ordinárias.

Tela 24
Módulo 01 – Conceito de Custo de Capital

Para efetuar o cálculo do custo de emissão de novas ações ordinárias, utilizamos a seguinte equação:


kn = (D1/Nn) + g

Onde:
kn = custo de emissão de novas ações ordinárias
D1 = dividendo a ser pago no próximo período
Nn = valor líquido recebido pela empresa quando da emissão primária do papel (ação ordinária)
g = taxa de crescimento constante dos dividendos

Exemplos

1) A Empresa JJ S/A deseja determinar o custo de novas ações ordinárias, kn. O preço de mercado de sua ação ordinária, P0, é igual a $40 cada. Os dividendos pagos aos acionistas nos últimos seis anos (2003-2008) foram os seguintes:

Ano
Dividendo
2003
$3,00
2004
$3,20
2005
$3,20
2006
$3,60
2007
$3,40
2008
$3,82

A empresa informa que os dividendos futuros deverão continuar crescendo tomando-se por base a média dos últimos seis anos. Para estimar o custo das novas ações ordinárias, kn, a empresa estima um underpricing de $2,0 por ação, e um custo associado à nova emissão de $2,2 por ação.

Resolução


Nesse exemplo, primeiro iremos operar o valor da taxa de crescimento, g.
g = [($3,82/$3,0)1/(n -1) -1] x100
g = [($3,82/$3,0)1/(6 -1) -1] x100
g = 4,9514448% ao ano ou 4,95% ao ano

Agora vamos operar o valor de D1. Nesse exemplo, o último dividendo pago ocorreu em 2008, portanto, D0 =$3,82, com isso:
D1 = D0(1+g)1
D1 = $3,82 (1+ 0,0495)
D1 = $4,00909 ou $4,01

Operar o valor líquido recebido pela JJ na operação de underwriting
Nn = P0 – underpricing – gastos de colocação
Nn = $40 - $2,0 - $2,2
Nn = $35,80

De posse dos valores apurados, estamos em condições de operar kn.
kn = (D1/NN) + g
kn = ($4,01/$35,80) + 0,0495
kn =0,161511173 x 100
kn = 16,1511173% ou 16,15%

Operando pela HP 12C
3,82 enter 3,0 ÷ 1 enter 5 ÷ yx 3,82 x 40 enter 2,0 - 2,2 - ÷ 3,82 enter 3,0 ÷ 1 enter 5 ÷ yx + 1 – 100 x
No visor da máquina teremos 16,15017440

A diferença entre o cálculo inicial e o da HP 12C deve-se ao processo de arredondamento.

Tela 25
Módulo 01 – Conceito de Custo de Capital

2) A Empresa Alpha pretende lançar no mercado novas ações ordinárias. Atualmente, essas ações estão sendo negociadas a $20,0 cada. Os analistas financeiros esperam que os dividendos que serão pagos no próximo ano sejam de $1,30, por ação. O lançamento destas ações terá um deságio de 5,75% e o custo de lançamento (underwriting) será de 2,75%, ambos sobre o valor atual das ações. Os dividendos da empresa têm crescido a uma taxa anual de 5,75% e, espera-se que esse crescimento continue no futuro. Calcule o custo da nova emissão de ações ordinárias da Empresa Alpha.

Resolução

3) A Empresa MBG está pretendendo lançar novas ações ordinárias no mercado. Suas ações ordinárias atuais estão cotadas a $45,0 cada; no último ano a MBG pagou dividendos de $4,20 por ação; haverá o deságio de $0,9 por ação e o custo de lançamento será de $1,8 por ação. A taxa de crescimento dos dividendos, esperada pelos analistas de investimento, é de 4,25% para sempre. Calcule o custo de emissão das novas ações ordinárias da MBG.

Resolução

4) A Empresa MB pretende lançar no mercado novas ações ordinárias. Atualmente, essas ações estão sendo negociadas a $120,0 cada. Os analistas financeiros esperam que os dividendos que serão pagos no próximo ano sejam de $9,50, por ação. O lançamento destas ações terá um deságio de 2,8% e o custo de lançamento (underwriting) será de 3,25%, ambos sobre o valor atual das ações. Os dividendos da MB, nos últimos três anos apresentaram uma taxa média anual de crescimento de 15%; os analistas estão projetando uma taxa anual constante de 6,5% no futuro. Calcule o custo da nova emissão de ações ordinárias da Empresa MB.

Resolução


Nesse exemplo nós dispomos:
g = 5,75%
D1 = $1,30 por ação
P0 = $20,0 por ação

Faz-se necessário operar NN para atender ao que está solicitado no exemplo.
NN = P0 [1 – (2,75% + 5,75%)]
NN = $20 (1 – 8,5%)
NN = $20 (1 – 0,085)
NN = $18,30

De posse dos valores apurados estamos em condições de operar kn.
kn = (D1/NN) + g
kn = ($1,30/$18,30) + 0,0575
kn =0,128538251 x 100
kn = 12,85382514% ou 12,85%

Operando pela HP 12C
1,30 enter 1 enter 0,0275 – 0,0575 – 20 x ÷ 0,0575 + 100 x
No visor da máquina teremos 12,85382514


Nesse exemplo nós dispomos:
g = 4,25%
D0 = $4,20 por ação
P0 = $45 por ação

Nesse exemplo se faz necessário calcular D1
D1 = D0(1+g)1
D1 = $4,20 (1 + 0,0425)
D1 = $4,3785

Vamos operar NN (valor líquido recebido pela empresa).
NN = P0 – deságio – gastos de lançamento
NN = $45 - $0,9 - $1,8
NN = $42,30

De posse dos valores apurados estamos em condições de operar kn.
kn = (D1/NN) + g
kn = ($4,3785/$42,30) + 0,0425
kn =0,146010638 x 100
kn = 14,6010638% ou 14,60%

Operando pela HP 12C
4,20 enter 1 enter 0,0425 + X 45 enter 0,9 –1,8 - ÷ 0,0425 + 100 x
No visor da máquina teremos 14,60106383


Nesse exemplo, dispomos dos seguintes dados:
g = 6,5%
D1 = $9,50 por ação
P0 = $120,0 por ação

Faz-se necessário operar NN para atender ao que está solicitado no exemplo.
NN = P0 [1 – (2,8% + 3,25%)]
NN = $120 (1 – 6,05%)
NN = $120 (1 – 0,0605)
NN = $112,74

De posse dos valores apurados, estamos em condições de operar kn.
kn = (D1/NN) + g
kn = ($9,50/$112,74) + 0,065
kn =0,149264680 x 100
kn = 14,9264680% ou 14,93%

Operando pela HP 12C
9,50 enter 1 enter 0,028 – 0,0325 – 120 x ÷ 0,065 + 100 x
No visor da máquina teremos 14,92646798

Tela 26
Módulo 01 – Conceito de Custo de Capital
2 - Custo dos lucros retidos - kr

Imagine uma empresa que tenha apresentado no último exercício social um lucro líquido igual a $100. Suponhamos que nesta empresa o índice de >Payout seja igual a 0,40, logo, o índice de retenção será igual a 0,60. Portanto, nesta empresa nós teríamos um pagamento de $40 em dividendos para os acionistas, onde cada acionista irá receber o seu dinheiro de acordo com sua participação no capital da empresa.

Ora, se a empresa desembolsar $40,00 dos $100 de lucro líquido, ela ficará com $60,00 para tocar os seus negócios. Vamos nos fixar nestes $60,00. Supondo que esse dinheiro seja incorporado ao capital social, o que irá acontecer? O capital social será aumentado em mais $60,00, com isso os acionistas serão premiados com uma bonificação em cima deste aumento, de acordo com a participação de cada um. Se o capital social, antes do aumento por incorporação de reservas, fosse de $500, a partir do aumento o capital social irá para $560. Pense num acionista que detenha 10% do capital social. Antes, ele participava com $50,00 sobre o capital social, agora ele terá $56,00. Observe que o acionista não desembolsou nenhum dinheiro para essa nova posição de capital social, pois o novo aumento do capital social foi com dinheiro gerado na própria empresa, porém, a participação do acionista se manteve em 10%, nesse caso, via bonificação de ações. Na verdade, o acionista abriu mão desse dinheiro para que o mesmo fosse mantido na empresa.

Muito bem, estes $60,00 já estavam dentro da empresa, pois, foram gerados pelas atividades (negócios) da própria empresa. Logo, a empresa, ao fazer o aumento do capital social de $500 para $560, não terá que contratar nenhum banco de investimento para gerenciar o lançamento do papel, e nenhum escritório de advocacia, assim como não terá de gastar com encontros com analistas de investimento e investidores etc.

Conclusão


Payout é a relação entre os dividendos distribuídos e o lucro líquido do exercício. O índice de payout mede a porcentagem do lucro líquido a ser distribuído aos acionistas de uma empresa.


Conclui-se que cálculo do custo dos lucros retidos será igual ao cálculo do custo das ações ordinárias já existentes, portanto, a equação para apurar o custo do lucro retido poderá ser operada também via modelo de Gordon, onde kr (custo dos lucros retidos) é igual a ks (custo da ação ordinária): kr = ks.

Tela 27
Módulo 01 – Conceito de Custo de Capital
Segundo Assaf Neto (2005) a justificativa básica para uma empresa reter lucros, em vez de distribuí-los a seus proprietários, é que ela possui alternativas de investimentos que remuneram o capital em termos de risco incorrido na decisão. Caso não surjam essas oportunidades financeiras, a orientação básica é de que a empresa promova a distribuição de seus lucros aos acionistas, de maneira que possam efetuar aplicações desses recursos em outras alternativas de investimento que prometam ganhos compatíveis ao risco assumido.

Equação:

kr = (D1/P0) + g

Exemplo

Usando os dados de cada empresa apresentados na tabela a seguir, calcule o custo de lucros retidos e o custo de novas ações ordinárias, empregando o modelo de avaliação com crescimento constante (modelo de Gordon).

Empresa
Preço corrente da ação
Taxa de crescimento dos dividendos
Dividendo
atual
Deságio por ação
Custo de
lançamento por ação
A
$50
4,0%
$4,5
2%*
3%*
B
$10
6,5%
$0,8
$0,15
3,5%*
C
$18,75
5,25%
$1,41
1,25%
$0,70
D
$19
3,0%
$1,52
$0,38
$0,85

*sobre o preço corrente da ação

Clique para ver as resoluções:


a) Custo dos lucros retidos
D0 =$4,5
P0 =$50
g = 4,0%
kr = (D1/P0) + g
kr = [$4,5 (1 + 0,04)/$50] + 0,04
kr = ($4,68/$50) + 0,04
kr = 0,1336 x 100
kr = $13,36%

b) Custo de emissão de novas ações ordinárias
D0 =$4,5
P0 =$50
g = 4,0%
NN = P0 – deságio – gastos de lançamento
NN = $50 (1 – 0,02 – 0,03)
NN = $47,50
kN = $[$4,5 (1 + 0,04)/$47,50] + 0,04
kN = ($4,68/$47,50) + 0,04
kN = 0,138526316 x 100
kN = 13,85%


a) Custo dos lucros retidos
D0 =$0,8
P0 =$10
g = 6,5%
kr = (D1/P0) + g
kr = [$0,8 (1 + 0,065)/$10] + 0,065
kr = ($0,852/$10) + 0,065
kr = 0,1502 x 100
kr = $15,02%

b) Custo de emissão de novas ações ordinárias
D0 =$0,8
P0 =$10
g = 6,5%
NN = P0 – deságio – gastos de lançamento
NN = $10 (1 – 0,035) - $0,15
NN = $9,5
kN = $[$0,8 (1 + 0,065)/$9,5] + 0,065
kN = ($0,852/$9,5) + 0,065
kN = 0,154684211 x 100
kN = 15,47%


a) Custo dos lucros retidos
D0 =$1,41
P0 =$18,75
g = 5,25%
kr = (D1/P0) + g
kr = [$1,41 (1 + 0,0525)/$18,75] + 0,0525
kr = ($1,484025/$18,75) + 0,0525
kr = 0,131648 x 100
kr = $13,16%

b) Custo de emissão de novas ações ordinárias
D0 =$1,41
P0 =$18,75
g = 5,25%
NN = P0 – deságio – gastos de lançamento
NN = $18,75 (1 – 0,0125) - $0,70
NN = $17,815625
kN = $[$1,41 (1 + 0,0525)/$17,815625] + 0,0525
kN = ($1,484025/$17,815625) + 0,0525
kN = 0,135799070 x 100
kN = 13,58%


a) Custo dos lucros retidos
D0 =$1,52
P0 =$19
g = 3,0%
kr = (D1/P0) + g
kr = [$1,52 (1 + 0,03)/$19] + 0,03
kr = ($1,5656/$19) + 0,03
kr = 0,1124 x 100
kr = $11,24%

b) Custo de emissão de novas ações ordinárias
D0 =$1,52
P0 =$19
g = 3,0%
NN = P0 – deságio – gastos de lançamento
NN = $19 -$0,38 - $0,85
NN = $17,77
kN = [$1,52 (1 + 0,03)/$17,77] + 0,03
kN = ($1,5656/$17,77) + 0,03
kN = 0,118103545 x 100
kN = 11,81%

Observamos nos quatro casos que o custo de lucros retidos foi sempre menor que o custo de emissão de novas ações ordinárias. Isso mostra que o deságio e os gastos de colocação tornam a emissão de novas ações mais cara que os lucros retidos. Não é à toa que empresas em fase de grande crescimento preferem reter o máximo de lucros possível (índice de payout muito baixo, quando não nulo) para poder tocar seus projetos de investimento com o máximo de dinheiro próprio, porque esse tipo de dinheiro costuma ser mais barato que a emissão de novas ações.

Tela 28
Módulo 01 – Conceito de Custo de Capital
3 - Custo das ações preferenciais - KP

O custo da ação preferencial aqui estudado irá se restringir àquelas ações preferenciais que no ato de sua emissão garantem aos investidores uma promessa de dividendos periódicos fixos. Em alguns casos, os dividendos de ações preferenciais são especificados em moeda por ano. Por exemplo, $2,0 por ação ou $3,0 por ação etc. Em outros casos, os dividendos preferenciais são estipulados sob a forma de uma taxa anual. Essa taxa representa a porcentagem do valor de face da ação que corresponde ao dividendo anual.

Segundo Brigham e Ehrhardt (2006) o custo componente da ação preferencial usado para calcular o Custo Médio Ponderado de Capital (CMPC) é o dividendo preferencial por ação, DP, dividido pelo preço líquido da emissão, NP, que é o valor que a empresa recebe depois de deduzir os custos de emissão.

Equação:


KP = DP/NP

Onde:

KP = custo da ação preferencial
DP = dividendo anual
NP = recebimento líquido auferido pela empresa com a venda da ação

O valor de NP será apurado da seguinte maneira:
NP = preço de venda da ação – despesas com lançamento

Por despesas de lançamento nós temos os desembolsos de caixa que a empresa irá experimentar em função do underwriting (comissão de underwriting para os intermediários financeiros, publicações em jornais, registro em bolsa de valores etc.).

Tela 29
Módulo 01 – Conceito de Custo de Capital
Segundo Gitman (2004) como os dividendos de ações preferenciais são pagos com os fluxos de caixa da empresa depois do IR/CS, não é necessário fazer nenhum ajuste por causa dos impostos.

Quando do lançamento de ações preferenciais poderá ocorrer as seguintes situações:

• O papel sair ao par, isto é, o preço de venda ser igual ao valor nominal ou de face.
• O papel sair com ágio, isto é, o preço de venda ser maior que o valor de face ou nominal.
• O papel sair com deságio, isto é, o preço de venda ser menor que o valor de face ou nominal.

Exemplos

1) Determinar o custo de cada uma das seguintes ações preferenciais:

Ação
Preferencial
Valor de face
Preço de venda
Custo de lançamento
Dividendo anual
 
$
$
$ ou %
$ ou %
A
100
102
9,5
12%
B
40
39
3%*
3,51
C
70
70
4,5
8,0
D
25
24,5
3,5%*
10%

* Preço de venda

Clique para ver as resoluções:


Observamos que o preço de venda apresenta-se > que o valor de face (valor nominal), logo, este papel está sendo operado com ágio, isto é, com prêmio.

DP = $100 x 0,12
DP = $12,0 por ação
NP = Preço de venda – desembolso de caixa quando da emissão primária
NP = $102 - $9,5
NP = $92,5
kP = ($12,0/$92,5) x 100
kP =12,97%


Observamos que o preço de venda apresenta-se < que o valor de face (valor nominal), logo, este papel está sendo operado com deságio.

DP = $3,51 por ação
NP = Preço de venda – desembolso de caixa quando da emissão primária
NP = $39 (1 – 0,03)
NP = $37,83
kP = ($3,51/$37,83) x 100
kP = 9,28%


Observamos que o preço de venda apresenta-se = ao valor de face (valor nominal), logo, este papel está sendo operado ao par.

DP = $8,0 por ação
NP = Preço de venda – desembolso de caixa quando da emissão primária
NP = $70,0 - $4,5
NP = $65,50
kP = ($8,0/$65,50) x 100
kP = 12,21%


Observamos que o preço de venda apresenta-se < que o valor de face (valor nominal), logo, este papel está sendo operado com deságio.

DP = $25 x 0,10
DP = $2,5 por ação
NP = Preço de venda – desembolso de caixa quando da emissão primária
NP = $24,5 (1 – 0,035)
NP = $23,64
kP = ($2,5/$23,64) x 100
kP = 10,57%

Tela 30
Módulo 01 – Conceito de Custo de Capital
2) A Empresa Alpha S/A pode emitir ações preferenciais perpétuas a um preço de $50 cada. Espera-se que a emissão pague um dividendo anual constante de $3,80 por ação. O custo da emissão está estimado em 5%. Qual é o custo da ação preferencial, kP, da empresa?

Resolução

3) A Empresa JJ S/A planeja emitir algumas ações preferenciais ao valor de face de $100 cada com um dividendo de 11%. A ação está sendo vendida no mercado por $97 e a empresa deve pagar custos de 4,5% do preço de mercado. Qual é o custo da ação preferencial da JJ?

Resolução

4) A Empresa TS S/A acaba de emitir ações preferenciais. O título promete um dividendo anual de 12% e se u valor de face é igual a $100. Foi vendido a $97,50 por ação. Além disso, devem ser pagos custos de lançamento de $2,50 por ação.

a) Calcule o custo de capital obtido com a emissão de ações preferenciais.
b) Se a empresa lançar a ação com dividendo anual de 10% e receber $90 após os custos de lançamento, qual será o custo?

Resolução


Nesse exemplo dispomos:
Preço de venda = $50
Dividendo perpétuo = $3,80
Custo de emissão = 5% (está implícito que esses 5% serão sobre o preço de venda).
NP = ?
kP = ?

Vamos operar inicialmente o valor de NP.
NP = $50 (1 – 0,05)
NP = $47,50
kP = ($3,80/$47,50) x 100
kP = 8%


Nesse exemplo dispomos:
Valor de face =$100
Dividendo anual = $100 x 0,11
Dividendo anual = $11
Preço de venda = $97
Valor líquido recebido pela empresa = $97 (1 – 0,045)
Valor líquido recebido pela empresa = $92,635

O custo da ação preferencial será:
KP = DP/NP
KP = ($11/$92,635) x 100
KP= 11,87%


a) Nesse exemplo dispomos:
Valor de face = $100
Dividendos perpétuos = $12% do valor de face
Preço de venda = $97,50
Custos de lançamento = $2,5

Vamos calcular o valor dos dividendos perpétuos:
DP = $100 x 0,12
DP = $12 por ação

Vamos calcular o valor líquido recebido pela empresa
NP = $97,50 - $2,5
NP = $95 por ação

Vamos calcular o custo da ação preferencial
kP = DP/NP
kP = ($12/$95) x 100
kP = 12,63%

b) Nessa pergunta dispomos:
Valor de face = $100
Dividendos perpétuos = $10% do valor de face
Valor líquido recebido =$90 por ação

Vamos calcular o valor dos dividendos perpétuos:
DP = $100 x 0,10
DP = $10 por ação

Vamos calcular o custo da ação preferencial
kP = DP/NP
kP = ($10/$90) x 100
kP = 11,11%

Tela 31
Módulo 01 – Conceito de Custo de Capital
Resumo

As empresas de capital aberto (S/A) podem lançar mão, a qualquer tempo, da oferta pública de novas ações ordinárias e preferenciais. A emissão de novas ações seguir um processo onde, num primeiro momento irá envolver a empresa emissora, os investidores e instituições financeiras especializadas na colocação de títulos no mercado de capitais.

Denomina-se operação de underwriting a emissão primária ou a oferta (leilão) pública de novas ações. Essa operação envolve a empresa – recebendo dinheiro e entregando novas ações–, o investidor – entregando dinheiro e recebendo novas ações–, e as instituições financeiras especializadas – recebendo uma comissão pelos serviços prestados para a empresa emissora.

O custo de emissão de novas ações ordinárias envolve emissão, corretagem, deságios e será calculado pelo modelo de crescimento constante dos dividendos (modelo de Gordon) com destaque para a o underpricing e para os gastos com a colocação do título. Para efetuar o cálculo do custo de emissão de novas ações ordinárias, utilizamos a seguinte equação: kn = (D1/Nn) + g.

O custo dos lucros retidos será calculado também pelo modelo de crescimento constante dos dividendos (modelo de Gordon) com o detalhe de que o tratamento será o mesmo das ações ordinárias já existentes.

O custo da ação preferencial quando o pagamento dos dividendos se caracteriza como sendo perpétuo (para sempre o mesmo valor) será calculado por meio da seguinte equação: kP = DP/NP.

Unidade 3 Módulo 3
Tela 32
Módulo 01 – Conceito de Custo de Capital

1 - Custo da dívida

Pense numa empresa de grande porte como a Gerdau S/A, atualmente, uma das maiores multinacionais brasileira, com unidades produtivas em 14 países, com destaque para América Latina e América do Norte. A Gerdau começou a operar em 1901, com a fábrica de Pregos Pontas de Paris, na cidade de Porto Alegre, Rio Grande do Sul. No início, como a maior parte das empresas, ela era pequena, com o tempo, foi crescendo e tomando porte até alcançar a posição de 13° maior produtor de aço do mundo. Certamente no começo do século XX a maior fonte do dinheiro que bancava os negócios tinha como origem o bolso dos seus proprietários, juntamente com os lucros gerados no negócio.

Um dado interessante é que a Gerdau, em seus 108 anos de existência, ainda não experimentou prejuízo um ano sequer, sempre operou no azul.

Será que ela irá conseguir passar pela crise atual no azul?

A maior parte das empresas, não todas, com o tempo, para poder dar saltos em termos de porte precisam buscar dinheiro fora do eixo proprietário/lucros retidos. Esse dinheiro que virá de fontes de fora da empresa poderá ser obtido de muitas fontes: bancos de fomento (BNDES, BRDE, BIRD, BID etc.), bancos comerciais, bancos múltiplos, bancos de investimento, investidores etc.

Tela 33
Módulo 01 – Conceito de Custo de Capital

Quais as diferenças entre o dinheiro oriundo do patrimônio líquido e o dinheiro oriundo de empréstimos e da emissão de dívida?

Segundo Damodaran (2004) a maioria das pessoas interpreta dívida e patrimônio líquido em termos de títulos e ações, mas a diferença entre dívida e patrimônio líquido está na natureza dos direitos sobre os fluxos de caixa da empresa.

Dinheiro oriundo do patrimônio líquido

Dinheiro oriundo de empréstimos e da emissão de dívida

Confere ao portador das ações direito sobre quaisquer fluxos de caixa residuais, após todos os outros compromissos terem sido atendidos.

Confere ao portador direito sobre um conjunto contratado de fluxos de caixa, normalmente o serviço da dívida: principal + encargos.

O acionista preferencial é o penúltimo na escala de direito sobre o ativo.
O acionista ordinário fica com o valor residual, ou seja, é o último a ter direitos sobre os ativos.

Tem um direito prévio tanto sobre os fluxos de caixa em uma base de período a período, para pagamentos de encargos (juros, variação cambial, correção monetária etc.) e do principal, quanto sobre os ativos da empresa, no caso de liquidação.

No caso do Brasil, nós temos os juros sobre capital próprio, que é uma remuneração para o acionista (um dividendo disfarçado) em que a empresa contabiliza o valor como despesa financeira, portanto, goza dos mesmos direitos da dívida em termos tributários. Os dividendos são determinados com base no lucro líquido, portanto, depois dos efeitos dos impostos (IR/Contribuição Social).

As leis tributárias, em geral, têm tratado as despesas financeiras de forma muito diversa, e muitas vezes com mais vantagens, do que os dividendos ou outros fluxos de caixa que resultam do patrimônio líquido.

As ações geralmente têm uma vida infinita.

A dívida normalmente tem uma data de vencimento fixa, quando o principal e os encargos devem ser pagos.

Finalmente, os investidores em ações, em virtude dos seus direitos sobre os fluxos de caixa residuais da empresa, têm controle total, ou muito abrangente, da administração da empresa. Os credores, por outro lado, têm um papel muito mais passivo na administração, exercendo, no máximo, o poder de veto sobre decisões financeiras importantes.


Tela 34
Módulo 01 – Conceito de Custo de Capital

2 - Fontes de dinheiro fora da empresa

Se você entrar no site da Gerdau S.A. (www.gerdau.com.br) e olhar as demonstrações financeiras encerradas em 31/12/2007 irá observar que as obrigações financeiras (nota explicativa n°14 – Empréstimos e Financiamentos) estão distribuídas nas seguintes moedas: real, dólar dos EUA, euro, peso colombiano, peso argentino e peso chileno. Na área internacional, costuma-se dizer que câmbio não é para amadores, isso é válido para as nossas multinacionais; deve ser um bom desafio operar no departamento financeiro da Gerdau. Além das diferentes moedas, você irá observar que a Gerdau deve para instituições financeiras, por exemplo, o BNDES e também para investidores, por exemplo, via debêntures. Qual a diferença entre esses dois tipos de credores?

Num empréstimo feito junto a um banco, no caso da Gerdau, o normal é que a garantia seja dada pela própria Gerdau, logo, o negócio fica entre a Gerdau e o banco. Suponha o Banco do Brasil (BB), se a Gerdau tiver problemas na geração de seu fluxo de caixa, o BB terá que arcar com as consequências, o risco de crédito será do BB.

Agora, pense numa debênture. Esse tipo de papel é um título de crédito emitido pelas empresas de capital de aberto e que é comprado por investidores (agentes econômicos com sobras de dinheiro em busca de oportunidades de aplicações financeiras). Se a Gerdau tiver qualquer tipo de problema no seu fluxo de caixa o risco será do investidor. Enquanto o empréstimo é feito diretamente com a instituição financeira, a emissão de dívida é feita via mercado de capitais.


Tela 35
Módulo 01 – Conceito de Custo de Capital

A emissão de dívida via mercado de capitais irá seguir o mesmo caminho da emissão de uma nova ação ordinária ou de uma nova ação preferencial, será via uma operação de underwriting. A empresa irá contratar os serviços de um ou mais bancos de investimentos, corretoras de valores mobiliários e, distribuidoras de valores mobiliários. Esses intermediários financeiros farão a ponta entre a empresa emissora e os potenciais investidores. O papel (a dívida) poderá ser emitido com ágio (quando o investidor paga pelo papel um valor maior que o valor de face ou valor nominal), deságio (quando o investidor paga pelo papel um valor menor que o valor de face, é o que predomina) e ao par (quando o papel é comprado pelo investidor pelo valor de face ou nominal).

Observe, para que uma empresa de capital aberto emita uma nova dívida se faz necessária a aprovação dos acionistas comuns (detentores de ações ordinárias); isso será feito em uma assembleia, onde normalmente é especificado o valor de face do papel e a taxa de juros nominal do papel (mais conhecida como juros de cupom). A empresa terá gastos com comissão de underwriting, escritório de advocacia, publicações em jornais, rodadas de reuniões com investidores (road show), solicitação de emissão nos órgãos reguladores (a CVM no Brasil; a SEC nos EUA), registro em bolsa de valores etc.


Tela 36
Módulo 01 – Conceito de Custo de Capital
3 - Custo de capital de terceiros de longo prazo - ki

Segundo Gitman (2004) o custo de capital de terceiros de longo prazo, ki, é o custo após o IR/CS (Imposto de Renda/Contribuição Social) hoje, de levantar recursos emprestados de longo prazo.

Equação para apurar o custo do capital de terceiros:

ki = kd x (1 – T)

Onde:

ki = custo de capital de terceiros depois dos impostos
kd = custo de capital de terceiros antes dos impostos
T = alíquota do IR/CS da empresa

Parte da dívida de longo prazo é assumida por meio da emissão de obrigações (emissão de dívida). Os recebimentos líquidos com a venda de uma obrigação ou de qualquer título são os fundos efetivamente recebidos com ela. Os gastos de lançamento – os gastos totais de emissão e venda de um título – reduzem os recebimentos líquidos proporcionados pela venda. Esses gastos aplicam-se a todos os lançamentos públicos de títulos: ações, debêntures, notes, bonds etc. Incluem dois componentes:

• gastos de underwriting;
• gastos administrativos.

Quando do lançamento de um título de dívida devemos ficar atentos para dois termos normalmente utilizados:

• valor de face ou valor nominal;
• cupom ou valor de cupom.


Remuneração recebida pelos bancos de investimento/corretoras/distribuidoras de valores mobiliários para realizar a colocação do papel.


Despesas do emitente, como gastos com serviços de assistência jurídica e contábil, impressão, publicações em jornais, road shows, registro em bolsas de valores e outros.


Valor de face é o valor de uma obrigação que aparece em seu certificado. Também é chamado de valor nominal ou principal.


Cupom são os juros nominais de um instrumento de dívida, isto é, os juros que aparecem no certificado.

Tela 37
Módulo 01 – Conceito de Custo de Capital

Suponha que a Empresa Alpha tenha convocado uma assembleia de acionistas para aprovar o lançamento (emissão) de novas debêntures não conversíveis, no mercado. Na assembleia de acionistas foi estipulado que cada debênture sairá com o valor nominal (face) de $1.000,00, tendo também sido estipulado juros de 15% ao ano. O valor aprovado foi de 20.000 novas debêntures onde os juros serão anuais e o pagamento do principal no final do contrato, isto é, daqui a cinco anos.

Neste caso, teríamos:

• o valor de face das debêntures = $1.000,00.
• o juro de cupom = 15% ao ano.

Exemplos

1) Calcule o custo da dívida depois dos impostos sob cada uma das seguintes condições:

Taxa de juros

Alíquota do imposto de renda
20%
0%
20%
24%
20%
28%
20%
34%

Resolução

2) Empréstimo bancário. A Empresa Alpha fez uma captação de dinheiro de longo prazo para tocar projetos de expansão em seu parque fabril pagando uma taxa nominal 12% ao ano. Esse dinheiro foi captado no BNDES tendo como agente repassador o Bradesco. Suponha que a alíquota do IR/CS da empresa seja de 30%, qual o custo desse empréstimo depois dos impostos?

Resolução


Nesse exemplo, basta aplicar a equação do custo da dívida; iremos observar que na medida em a alíquota dos impostos aumenta, menor será o custo da dívida depois dos impostos.

Informações fornecidas:
Kd = 20% ao ano
T = 0%; 24%; 28% e 34%
Ki = ?

Vamos para os cálculos:
Para T= 0%
Ki = Kd (1 – T)
Ki = 20 (1 – 0)
Ki = 20%

Para T= 24%
Ki = Kd (1 – T)
Ki = 20 (1 – 0,24)
Ki = 15,20%
 Para T= 28%
Ki = Kd (1 – T)
Ki = 20 (1 – 0,28)
Ki = 14,40%
 Para T= 34%
Ki = Kd (1 – T)
Ki = 20 (1 – 0,34)
Ki = 13,20%



Ki = Kd (1 – T)
Nesse exemplo temos:
Kd = 12% ao ano
T = 30%
Ki = 12 (1 – 0,30)
Ki = 8,4% ao ano.

Tela 38
Módulo 01 – Conceito de Custo de Capital

3) Emissão de dívida. A Empresa Alpha S/A acabou de emitir um título de dívida de longo prazo com as seguintes características:

 

Valor nominal ou de Face
Juros de cupom % ao ano
Prazo em anos
Pagamento dos juros
Deságio sobre o valor de face
Comissão de underwriting e outros gastos/Face

$1.000

13%

5

anual

0,5%

4%

A alíquota do IR/CS da empresa foi estimada em 34%.

Resolução

4) Emissão de dívida. A Empresa JJ tem condições de captar um volume ilimitado de capital de terceiros vendendo obrigações com valor de face de $1.000, cupom de 10% ao ano e prazo de 10 anos. Os pagamentos de juros seriam anuais. Para vender as obrigações o papel sofrerá um deságio de 0,25% sobre o valor de face e os gastos com comissão de underwriting e outras despesas serão de 2% do valor de face. A alíquota do IR/CS da JJ é de 34%. Calcule o custo anual da dívida antes do IR/CS, depois do IR/CS, bem como, o retorno anual para o investidor (opere com a hipótese de o investidor está isento do IR).

Resolução

5) Com base em Brigham e Ehrhardt (2006). Os títulos de dívida da Empresa Alpha S/A têm nove anos remanescentes até o vencimento. Os juros são pagos anualmente, os títulos de dívida têm um valor nominal de $1.000 e a taxa de juros cupom é de 8%. Os títulos de dívida têm um rendimento até o vencimento de 9,75%. Qual é o preço de mercado atual desses títulos de dívida?

Resolução

Tela 39
Unidade 01 - Matemática Básica

Nesse exemplo nós iremos fazer algumas operações:

a) Calcular o valor líquido que a empresa irá receber pela oferta pública dos títulos.
b) Calcular o valor dos juros anuais.
c) Calcular o valor do principal + juros no último ano
d) Apresentar o DFC da operação
e) Calcular o custo da dívida antes dos impostos, kd. Nesse cálculo iremos seguir o mesmo caminho do observado quando estimamos a IRR.
f) Calcular o custo da dívida depois dos impostos, ki.

O valor de face da obrigação é de $1.000, porém, o papel foi comprado pelos investidores por um preço menor. Por quê? O papel foi comprado por:

$1.000 (1 – 0,005) = $995 cada, isto é, operou com um deságio de $5 por título. Isto ocorreu porque os investidores não aceitam ganhar apenas 13% ao ano, eles querem ganhar mais do que 13% ao ano, logo, o papel neste caso, sofre deságio, ou seja, o investidor desembolsa um valor menor do que o valor de face estipulado no título.

Valor líquido (VL) que irá entrar no caixa da empresa, por título:

VL = Valor de face ± ágio/deságio – comissão de underwriting – outros gastos de lançamento
VL = $1.000 [1 – (0,5/100) – (4/100)]
VL = $1000 (1 – 0,005 – 0,04)
VL = $955

Cálculo dos juros anuais:

O cálculo dos juros será sempre calculado sobre o valor de face (não interessa se o papel saiu com ágio ou com deságio) e com base na taxa de cupom, portanto:
j = $1.000 (13/100)
j = $130

Tela 40
Unidade 01 - Matemática Básica

Cálculo do valor que será desembolsado no último ano (P + J).

P+J = Valor de face + juros
P+J = $1.000 + $130
P+J = $1.130

DFC dessa emissão de dívida:

Cálculo do custo da dívida antes dos impostos, kd.

$955 - [$130/(1+ kd)1 + $130/(1+ kd)2+.....+ $1.130/(1+ kd)5] =$0
kd = IRR

Utilizando-se uma máquina financeira (HP 12 C) encontramos:

955 g CF0
130 CHS g CFJ
4 g NJ
1130 CHS g CFJ
f IRR
No visor da máquina teremos 14,32089989
Portanto: kd = 14,32% ao ano

Cálculo do custo da dívida depois dos impostos, ki.

Ki = Kd (1 – T)
Ki = 14,32 (1 – 0,34)
Ki = 9,45% ao ano

Tela 41
Unidade 01 - Matemática Básica

Nesse exemplo primeiro iremos operar o custo da dívida para a empresa para, logo a seguir operar a taxa de juros recebida pelo investidor.

Valor líquido (VL) que irá entrar no caixa da empresa, por título:

VL = Valor de face ± ágio/deságio – comissão de underwriting – outros gastos de lançamento
VL = $1.000 [1 – (0,25/100) – (2/100)]
VL = $1000 (1 – 0,0025 – 0,02)
VL = $977,50

Cálculo dos juros anuais:

O cálculo dos juros será sempre calculado sobre o valor de face (não interessa se o papel saiu com ágio ou com deságio) e com base na taxa de cupom, portanto:
j = $1.000 (10/100)
j = $100

Cálculo do valor que será desembolsado no último ano (P + J).

P+J = Valor de face + juros
P+J = $1.000 + $100
P+J = $1.100

DFC dessa emissão de dívida:

Tela 42
Unidade 01 - Matemática Básica

Cálculo do custo da dívida antes dos impostos, kd.

$977,50 - [$100/(1+ kd)1 + $100/(1+ kd)2 +.......+ $1.100/(1+ kd)10] =$0
kd = IRR

Utilizando-se uma máquina financeira (HP 12 C) encontramos:

977,5 g CF0
100 CHS g CFJ
9 g NJ
1100 CHS g CFJ
f IRR
No visor da máquina teremos 10,3720499
Portanto: kd = 10,37 % ao ano

Cálculo do custo da dívida depois dos impostos, ki.

Ki = Kd (1 – T)
Ki = 10,37 (1 – 0,34)
Ki = 6,84% ao ano

Vamos agora operar a taxa de juros ganha pelo investidor, ou seja, pelo comprador do papel (obrigação).

Valor desembolsado pelo investidor por obrigação:
VD = valor de face ± ágio/deságio
VD = $1.000 x (1 – 0,25/100)
VD = $997,50

O valor dos juros anuais e o valor que será recebido no último ano serão iguais aos cálculos já operados para a empresa, portanto:

Juros anuais = $100
Recebimento no último ano= $1.100
O DFC para o investidor será:

Cálculo da taxa de retorno para o investidor

[$100/(1+ kd)1 + $100/(1+ kd)2 +.......+ $1.100/(1+ kd)10) - $997,50 =$0
kd = IRR

Utilizando-se uma máquina financeira (HP 12 C) encontramos:

997,5 CHS g CF0
100 g CFJ
9 g NJ
1100 g CFJ
f IRR
No visor da máquina teremos 10,04075761
Portanto: kd =10,04 % ao ano

Tela 43
Unidade 01 - Matemática Básica

DFC da divida

Nesse exemplo o caminho será trazer todos os valores futuros para valor presente, o caminho mais indicado é a aplicação do fator de valor presente, FPV.

Você pode operar o FPV por dois caminhos:

FPV = 1 – (1 + i)-n/i
ou
FPV = (1 + i)n -1/(1 + i)n x i

Por uma questão de gosto iremos operar a primeira fórmula.

Juros anuais = $1.000 x 0,08
Juros anuais = $80
Valor a ser desembolsado no último ano= ($1.000 + $80)
Valor a ser desembolsado no último ano = $1.080

Portanto:

PV = (PMT x FPVi,n-1) + (P + J)/(1+i)n
PMT = valor dos juros anuais
i = rendimento dos títulos
n-1 = 9 -1 = 8 anos
n = 9
P + j = Valor de face + juros do último ano
PV = $80 x [1 – (1 + 0,0975)-8/0,0975] + [$1.080/(1 + 0,0975)9]
PV = $430,71 + $467,49
PV = $898,19 (preço de mercado atual dos papéis).

Tela 44
Módulo 01 – Conceito de Custo de Capital

6) Com base em Brigham e Ehrhardt (2006). Os títulos de dívida da Empresa Alpha têm oito anos remanescentes até o vencimento. Os juros são pagos anualmente, os títulos de dívida têm um valor nominal de $1.000 e a taxa de juros cupom é de 10%. Os títulos de dívida são vendidos ao preço de $850. Qual é o seu rendimento até o vencimento?

Resolução

7) Com base em Brigham e Ehrhardt (2006). Os títulos de dívida da Empresa Alpha vão vencer em dezesseis anos. Os títulos de dívida têm um valor de face de $1.000 e uma taxa cupom de 7,0% paga semestralmente. O preço do título de dívida é $1.070. Os títulos de dívida são resgatáveis em oito anos ao preço de resgate antecipado de $1.035. Qual é o rendimento até o vencimento? Qual é o rendimento até o resgate antecipado?

Resolução


DFC da dívida

Nesse exemplo o caminho será encontrar a IRR (TIR), para tanto, vamos indicar os cálculos e operar a HP 12C (o caminho mais rápido e simples você já sabe: operar via Excel).

O exemplo informa:
Valor líquido recebido pelo papel = PV = $850
Juros anuais = $1.000 x 0,10
Juros anuais = $100
Valor no último ano = P + J
Valor no último ano = $1.000 + $100
Valor no último ano = $1.100
IRR = %?

Indicação do cálculo:
$850 – [$100(1+r)1 + $100(1+r)2 + $100(1+r)3 +.... + $100(1+r)7 + $1.100(1+r)8] = $0

Operando via HP 12C
850 g CF0
100 CHS g CFj
7 g Nj
1100 CHS g CFj
f IRR
No visor da máquina encontramos 13,14089257
O rendimento do papel até o vencimento é igual a 13,14% ao ano.

Tela 45
Unidade 01 - Matemática Básica

Nesse exemplo o aluno precisa ficar atento para a taxa de cupom. Aqueles 7% estão ao ano e não ao semestre. Para o cálculo dos juros semestrais se faz necessário apurar a taxa de juro semestral, nesse caso o cálculo será dessa maneira:

Taxa semestral = Taxa anual/2
Taxa semestral = 7,0/2
Taxa semestral = 3,5% a.s.

Vamos para o DFC da dívida supondo o resgate no vencimento do papel, ou seja, em quinze anos. Observe que nesse exemplo o papel está sendo negociado no mercado com ágio ($1.070 > $1.000).

DFC da dívida

O exemplo informa:

Valor líquido recebido pelo papel = PV = $1.070
Juros semestrais = $1.000 x 0,035
Juros semestrais = $35
Valor no último semestre = P + J
Valor no último semestre = $1.000 + $35
Valor no último semestre = $1.035
IRR = %?

Indicação do cálculo:

$1.070 – [$35(1+r)1 + $35(1+r)2 + $35(1+r)3 +.... + $35(1+r)31 + $1.035(1+r)32] = $0

Operando via HP 12C

1070 g CF0
35 CHS g CFj
31 g Nj
1035 CHS g CFj
f IRR
No visor da máquina encontramos 3,149645482


Tela 46
Unidade 01 - Matemática Básica

O rendimento do papel até o vencimento é igual a 3,149645482% ao semestre.

Ocorre que a taxa de rendimento do papel precisa ser expressa ao ano, portanto:

IRR = [(1 + 0,03149645482)2 -1] x 100
IRR = 6,3984937% ao ano ou 6,40% ao ano.

Observe que a taxa efetiva é menor que a taxa de cupom, por quê? Porque o papel está sendo operado no mercado com ágio.

Vamos para a hipótese de o investidor resgatar o papel antes do vencimento, agora iremos operar o cálculo direto na HP 12C, ou seja, iremos até a taxa efetiva ao ano.

DFC da dívida

O exemplo informa:

Valor líquido recebido pelo papel = PV = $1.035
Juros semestrais = $1.000 x 0,035
Juros semestrais = $35
Valor no último semestre = P + J
Valor no último semestre = $1.000 + $35
Valor no último semestre = $1.035
IRR = %?

Indicação do cálculo:

$1.035 – [$35(1+r)1 + $35(1+r)2 + $35(1+r)3 +.... + $35(1+r)15 + $1.035(1+r)16] = $0

Operando via HP 12C
1035 g CF0
35 CHS g CFj
15 g Nj
1035 CHS g CFj
f IRR
100 ÷ 1 + 2 yx 1 – 100 x
No visor da máquina encontramos 6,5369234
O rendimento do papel para vencimento antecipado é igual a 6,54% ao ano.

Tela 47
Módulo 01 – Conceito de Custo de Capital

Resumo

A captação de empréstimo por parte de uma empresa junto à instituição financeira irá gerar uma obrigação da empresa tomadora com a instituição financeira; na maior parte das vezes, o risco da operação será da instituição que concedeu o empréstimo. Por sua vez, a captação de dinheiro por parte de uma empresa no mercado de capitais, por meio da emissão de dívida será coordenada por instituições financeiras especializadas na colocação de títulos de dívida junto aos investidores. Tais instituições são os bancos de investimento, as corretoras de títulos e valores mobiliários e as distribuidoras de títulos e valores mobiliários. O serviço dessas instituições será pago pela empresa emissora de dívida por meio de uma comissão, também conhecida por comissão de underwriting.

No ato do leilão dos títulos de dívida, poderá acontecer de o papel ser negociado com: ágio, deságio e ao par.

A maioria das pessoas interpreta dívida e patrimônio líquido em termos de títulos e ações, mas a diferença entre dívida e patrimônio líquido está na natureza dos direitos sobre os fluxos de caixa da empresa.

O custo de capital de terceiros de longo prazo, ki, é o custo após o IR/CS (Imposto de Renda/Contribuição Social) hoje, de levantar recursos emprestados de longo prazo.


Unidade 3 Módulo 4
Tela 48
Módulo 01 – Conceito de Custo de Capital
1 - Custo médio ponderado de capital – Ka

Vimos como se calcula o custo das diversas fontes de dinheiro que uma empresa pode vir a utilizar: custo da dívida, custo da ação ordinária e custo da ação preferencial. Agora, precisamos operar o custo de capital de uma empresa olhando ao mesmo tempo para a composição da(s) fonte(s) utilizada(s) pela empresa. Se pensarmos numa sociedade por ações, podemos encontrar as seguintes composições de capital:

a) Ações ordinárias + ações preferenciais + dívida
b) Ações ordinárias + dívida
c) Exclusivamente ações ordinárias.

Portanto, será possível nos defrontar com empresas onde a fonte de dinheiro seja exclusivamente de ações ordinárias. O que não será possível, numa sociedade por ações, é uma situação onde não exista a participação de ações ordinárias.

Para apurarmos o custo de capital ou custo médio ponderado de capital de uma empresa será necessário dispormos do custo específico de cada fonte de dinheiro utilizada pela empresa e o peso (a proporção) de cada uma das fontes. Iremos representar o peso de cada fonte da seguinte maneira:


peso das ações ordinárias = ws
peso das ações preferenciais = wp
peso da dívida/empréstimos = wi
wi + wp + ws = 1,0 ou 100%

Segundo Gitman (2004) os pesos podem ser calculados com base no valor contábil ou no valor de mercado e podem ser usadas proporções históricas ou ideais.


Os pesos baseados em valores contábeis usam os dados contidos nas demonstrações financeiras para medir a proporção de cada tipo de capital na estrutura financeira da empresa.


Os pesos baseados em valores de mercado medem a proporção de cada tipo de capital ao preço de mercado dos títulos envolvidos. Os pesos baseados em valores de mercado são preferíveis aos pesos baseados em valores contábeis.

Tela 49
Módulo 01 – Conceito de Custo de Capital

O custo médio ponderado de capital, ka, reflete o custo médio futuro de fundos esperado no longo prazo. É obtido multiplicando o custo de cada tipo específico de capital por sua proporção na estrutura de capital da empresa.

A equação que especifica o CMPC é a seguinte:


ka =(wi x ki) + (wP x kP) + (ws x ks)

Onde:

ka = custo médio ponderado de capital
ki = custo da dívida depois dos impostos
wi = peso da dívida
kp = custo da ação preferencial
wp = peso da ação preferencial
ks = custo da ação ordinária
ws = peso da ação ordinária

Segundo Brigham e Ehrhardt (2006) o custo de capital é afetado por uma variedade de fatores. Alguns estão além do controle da empresa, mas outros são influenciados por suas políticas de financiamento e de investimento.

Custo de capital da empresa

Fatores que a empresa não pode controlar

Fatores que a empresa pode controlar

nível das taxas de juros

política de estrutura de capital

prêmio pelo risco de mercado

política de dividendos
impostos política de investimento (orçamento de capital)

Tela 50
Módulo 01 – Conceito de Custo de Capital

Exemplos

1) Suponha uma empresa que apresente, a preços de mercado, a seguinte composição de fontes de dinheiro bancando os seus projetos de investimento: Ações ordinárias = $100; Ações preferenciais =$40 e Dívida = $60. Qual o peso de cada fonte?

Resolução

2) Considere o quadro abaixo, com a estrutura financeira existente da Empresa ALPHA. O Valor do Capital Próprio da empresa é de R$ 2.000.000,00.

FONTE
CUSTO(%a.a)
PROPORÇÃO (%)

Debêntures

12,5

15

Empréstimos

13,75

30

Ações Preferenciais

17

10

Capital Próprio

18

45

Calcule o custo médio ponderado de capital.

Resolução

3) A Empresa Gama S/A compilou as informações apresentadas na seguinte tabela:

Fonte de capital

Valor contábil

Valor de mercado

Custo depois do imposto de renda

Dívida de longo prazo

$3.150

$3.780

8,0%

Ações preferenciais

$ 700

$ 805

14%

Ações ordinárias

$3.150

$3.654

17%

a) Calcule o custo médio ponderado de capital usando como peso os valores contábeis.
b) Calcule o custo médio ponderado de capital usando como peso os valores de mercado.
c) Compare as respostas obtidas nos itens a e b. Explique as diferenças.

Resolução


Primeiro será necessário operar o valor do capital total:
Capital total = $100 + $40+ $60
Capital total = $200

De posse do capital total será possível operar o peso de cada fonte de dinheiro utilizada pela empresa:

wi = $60/$200 = 0,30 ou 30%
wp = $40/$200 = 0,20 ou 20%
ws = $100/$200 = 0,50 ou 50%

Observe que a soma dos pesos será igual a 1,0 ou 100%, veja:
0,30 + 0,20 + 0,50 = 1,0 ou 30% + 40% +100% = 100%


Observe que a soma dos pesos será:
15% + 30% + 10% + 45% = 100%
ka = (12,5 x 0,15) + (13,75 x 0,30) + (17 x 0,10) +(18 x 0,45)
ka = 15,80%

>


a) Custo de capital com base nos valores contábeis (pesos).

Primeiro será preciso calcular o valor do capital total.
Capital total = $3.150 + $700 + $3.150
Capital total = $7.000

De posse do capital total podemos calcular o peso de cada fonte:
wi = $3.150/$7.000 = 0,45 ou 45%
wP = $700/$7.000 = 0,10 ou 10%
wS = $3.150/$7.000 = 0,45 ou 45%

De posse dos pesos calculados e dos custos de cada fonte (fornecidos no exemplo) podemos calcular o CMPC:
ka = (8 x 0,45) + (14 x 0,10) + (17 x 0,45)
ka = 12,65%

Observe, tomando por base os pesos com valor contábil, nessa empresa novos projetos de investimento seriam estudados somente com IRR (TIR) > 12,6% ao ano, apenas assim irá ocorrer VPL >$0. A riqueza dos acionistas,dessa maneira, poderá ser maximizada.

b) Custo de capital com base nos valores de mercado (pesos).

Primeiro será preciso calcular o valor do capital total.
Capital total = $3.780 + $805 + $3.654
Capital total = $ 8.239

De posse do capital total podemos calcular o peso de cada fonte:
wi = $3.780/$8.239 = 0,4588 ou 45,88%
wP = $805/$8.239 = 0,0977ou 9,77%
wS = $3.654/$8.239 = 0,4435 ou 44,35%

De posse dos pesos calculados e dos custos de cada fonte (fornecidos no exemplo) podemos calcular o CMPC:
ka = (8 x 0,4588) + (14 x 0,0977) + (17 x 0,4435)
ka = 12,58%

Observe que, tomando por base os pesos com valor de mercado, nessa empresa novos projetos de investimento seriam estudados somente com IRR (TIR) > 12,58% ao ano, apenas assim irá ocorrer VPL >$0. A riqueza dos acionistas, dessa maneira, poderá ser maximizada.

c) Nesse exemplo, o ágio sobre o papéis da dívida estão acima do ágio das ações ordinárias e preferenciais, como o custo da dívida é menor que o custo das outras duas fontes ela puxa para baixo o custo médio ponderado de capital. Independente disso, se a empresa vier a ser vendida, ela será avaliada a preço de mercado, por esse motivo, o cálculo, tomando os pesos a preço de mercado, se aproxima mais do mundo real dos negócios.
Tela 51
Módulo 01 – Conceito de Custo de Capital

4) Na Empresa Alpha S/A o valor contábil das dívidas é igual a $90 milhões. Atualmente, os títulos de dívida estão sendo negociados a 110% do valor contábil e rendem, antes dos impostos, 13% ao ano. Os 6 milhões de ações da empresa estão sendo negociados a $19 por unidade. O retorno exigido pelos acionistas é igual a 19%. A alíquota do imposto de renda da empresa é de 34%. Calcule o custo médio ponderado de capital da Empresa Alpha. Responda: novos projetos de investimento nessa empresa seriam analisados em que condições?

Resolução

5) Vamos supor que no exemplo anterior (N° 4) ao invés de a dívida estar sendo negociada a 110% do valor contábil ela estivesse sendo negociada a 95% do valor contábil, o que iria acontecer com as nossas perguntas?

Resolução

6) A Empresa XYZ S/A possui uma estrutura de capital desejada de 51% de ações ordinárias, 9% de ações preferenciais e 40% de títulos de dívida. O custo das ações ordinárias é de 21%, o custo das ações preferenciais é de 18% e o custo de capital de terceiros antes dos impostos é de 12%. A alíquota do IR/CS é igual a 34%. Qual é o CMPC da JJ? Qual a condição para a análise de novos projetos de investimento nessa empresa?

Resolução

7) Com base nas seguintes informações sobre a Empresa Alpha S/A descubra seu WACC (weighted average cost of capital). Suponha que a alíquota de IR/CS da empresa seja de 34%. Nessa empresa novos projetos de investimento serão analisados em que condições?

Dívida: 100 obrigações com cupom de 7,5%, valor de face de $1.000, prazo de cinco anos, cotadas a 104% de seu valor nominal; sendo o pagamento dos juros anuais.

Ações ordinárias: 10.000 ações, vendidas a $15 cada; beta igual a 0,8; taxa livre de risco de 10% e prêmio pelo risco de mercado igual a 4,5%.

Ações preferenciais: 3.000 ações de $13 com dividendos de 11%.

Resolução


Nesse exemplo, nós temos:
Ks = 19% ao ano
Kd = 13% ao ano
T = 34%

Como já dispomos do custo da ação ordinária, vamos operar logo o custo da dívida depois dos impostos:
ki kd (1 – T)
ki 13 ( 1 – 0,34)
ki 8,58%

Vamos agora para o cálculo do peso de cada fonte de dinheiro de longo prazo:
Valor de mercado da dívida = $90.000.000 x (110/100)
Valor de mercado da dívida = $99.000.000
Valor de mercado das ações = 6.000.000 x $19
Valor de mercado das ações = $114.000.000

De posse do valor de cada fonte precisamos calcular agora o valor do capital total para termos condições de apurar os pesos.

Capital total = $ 99.000.000 + $114.000.000
Capital total = $ 213.000.000

Peso da dívida = $99/213 = 0,4648 ou 46,48%
Peso da ação ordinária = $114/213 = 0,5352 ou 53,52%

Estamos com o custo de cada fonte e o seu respectivo peso, vamos para o CPMC:
ka = (8,58 x 0,4648) + (19 x 0,5352)
ka = 14,16%

Nessa empresa, novos projetos de investimento terão que apresentar IRR > 14,16% ao ano, isso irá possibilitar que os projetos apresentem VPL > $0, somente dessa maneira será possível o alcance da maximização da riqueza dos acionistas da empresa.


Nesse caso, o valor da dívida seria:
Valor da dívida = $90.000.000 x (95/100)
Valor da dívida = $85.500.000

Com isso, teremos uma nova posição para o valor total e o peso das fontes de dinheiro:
Capital total = $ 85.500.000 + $114.000.000
Capital total = $199.500.000

Peso da dívida = $85,5/199,5 = 0,4286 ou 42,86%
Peso da ação ordinária = $114/199,5 = 0,5714 ou 57,14%
Com isso o custo de capital ficará em:
ka = (8,58 x 0,4286) + (19 x 0,5714)
ka = 14,53%

Com isso, novos projetos de investimento terão de apresentar IRR > 14,53% ao ano, ou seja, ficou mais difícil para a empresa porque quanto maior o custo de capital, menores as chances de novos projetos de investimento. Sabemos que a saída de uma situação de ágio para um deságio na dívida certamente iria afetar o custo da dívida, os investidores iriam exigir uma taxa maior que 13%. O mesmo iria acontecer com as ações, além de exigir um retorno maior, certamente o preço das ações iria cair para um valor menor que $14 por ação, em síntese, o valor da empresa seria afetado, portanto, o CMPC certamente seria maior que 14,53% ao ano.


Nesse exemplo, nos dispomos:
Ks = 21%
KP = 18%
Kd = 12%
wi = 0,40 ou 40%
wP = 0,09 ou 9%
wS = 0,51 ou 51%

Precisamos calcular o custo da dívida, depois dos impostos:
ki Kd (1 – T)
ki 12 (1 – 0,34)
ki 7,92%

Agora, estamos em condições de calcular o CMPC:
ka (7,92 x 0,40) + (18 x 0,09) + (0,51 x 21)
ka 15,50% ao ano

Nessa empresa, novos projetos de investimento deverão apresentar IRR >15,50% ao ano. Desta forma, esses projetos apresentarão VPL >$0 e assim será possível a maximização da riqueza dos acionistas da empresa.

Seria interessante o aumento do peso da dívida na estrutura de capital dessa empresa já que o custo da dívida é menor que as outras duas fontes de dinheiro?

Vamos supor que o peso da dívida fosse para 50% e que o peso da ação ordinária caísse para 41%, sem qualquer outra alteração nos demais valores inicialmente fornecidos, qual seria o novo CMPC?
ka (7,92 x 0,50) + (18 x 0,09) + (0,41 x 21)
ka 14,19% ao ano

De forma estática percebemos uma melhora no CMPC da empresa, com isso, ela se tornaria mais competitiva porque ao invés de IRR > 15,50% ao ano a nova situação traria a IRR para uma taxa menor, IRR >14,19%. Ocorre que existe um pequeno grande problema: a dívida exige geração de fluxo de caixa para o pagamento do serviço da dívida (Principal + encargos), independentemente de a empresa atingir ou não as suas vendas estimadas. Quanto maior o peso da dívida maior será o risco de crédito da empresa. Conclusão: o risco da empresa tende a aumentar; os valores que se mantiveram no novo cálculo não ficariam estáticos, certamente a taxa de juros exigida pelos investidores e banqueiros seria maior que 12% ao ano, isso para não mencionar o reflexos sobre o preço das ações. Portanto, todo cuidado é pouco quando pensarmos em aumentar o peso da dívida, levando em conta apenas o fato de que ela costuma ser mais barata que as outras duas fontes de dinheiro.


Tela 52
Unidade 01 - Matemática Básica
a) Vamos inicialmente calcular os pesos:

Valor da dívida = 100 x $1000 x (104/100)
Valor da dívida = $104.000
Valor das ações preferenciais = 3.000 x $13
Valor das ações preferenciais = $39.000
Valor das ações ordinárias = 10.000 x $15
Valor das ações ordinárias = $150.000
Agora vamos operar o valor do capital total:
Capital total = $104.000 + $39.000 + $150.000
Capital total = $293.000

De posse do valor de cada fonte individual e do capital total vamos para os pesos das fontes de dinheiro de longo prazo:

wi = 104/293
wi = 0,36 ou 36%
wp = 39/293
wp = 0,13 ou 13%
ws = 150/293
ws = 0,51 ou 51%

b) Operar o custo da ação preferencial

kp = 11% (fornecido no exercício)

c) Operar o custo da ação ordinária: nesse exemplo estamos operando o CAPM:

Ks = RF + [ß (KM – RF)]
ks = 10 + (0,8 x 4,5)
ks = 13,6%

d) Operar o custo da dívida

Valor líquido = $1000 x (104/100)
Valor líquido = $1.040
Juros anuais = $1.000 x (7,5/100)
Juros anuais = $75
Valor a ser pago no Ano 5 = $1.000 + $75
Valor a ser pago no Ano 5 = $1.075

DFC da dívida

Tela 53
Unidade 01 - Matemática Básica

Custo da dívida antes dos impostos, kd.

$1.040 –[$75/(1 + kd)1+$75/(1 + kd)2+.....+$1.075/(1 + kd)5] =$0

Observe, o valor inicial é maior que o valor de face ($1.040 > $1.000) enquanto que os juros foram operados sobre o valor de face, isso significa que o custo nominal para a empresa será menor que a taxa de cupom.

Operando o custo da dívida antes dos impostos via HP 12C

1040 g CF0
75 CHS g CFJ
4 g NJ
1075 CHS g CFJ
f IRR
No visor da máquina teremos 6,536513142
Portanto: kd = 6,54% ao ano

Vamos operar o custo da dívida depois dos impostos:

Ki = kd (1 – T)
Ki = 6,54 (1 – 0,34)
Ki = 4,32%

e) Agora, estamos em condições de operar o CMPC da empresa, pois, já dispomos dos pesos e do custo de cada fonte de dinheiro de longo prazo.

Ka = (ki x wi) + (kp x wP) + (ks x ws)
Ka = (4,32 x 0,36) + (11 x 0,13) + (13,6 x 0,51)
Ka = 9,92% ao ano

Novos projetos de investimento deverão apresentar taxa de retorno > 9,92%, com isso será possível alcançar VPL >$0 e atender ao objetivo de uma empresa em finanças corporativas: a maximização da riqueza do(s) proprietário(s).

Vamos treinar um pouco mais o DFC. Suponhamos que os papéis da empresa estivessem sendo cotados a 100% do valor de face, como ficaria o DFC da dívida?

DFC da dívida

Você irá observar que o custo nominal da dívida antes dos impostos será exatamente igual à taxa de cupom, veja:

Custo da dívida antes dos impostos, kd.

$1.000 –[$75/(1 + kd)1+$75/(1 + kd)2+.....+$1.075/(1 + kd)5] =$0

Observe, o valor inicial é igual ao valor de face ($1.000 = $1.000), por quê?

Valor líquido = $1.000 x (100/100)
Valor líquido = $1.000

Operando o custo da dívida antes dos impostos via HP 12C

1000 g CF0
75 CHS g CFJ
4 g NJ
1075 CHS g CFJ
f IRR
No visor da máquina teremos 7,500000000
Portanto: kd =7,5% ao ano

Tela 54
Unidade 01 - Matemática Básica
Vamos avançar um pouco mais no DFC, suponhamos agora que o papel esteja sendo negociado a 96% do valor de face, isso irá implicar em um kd maior que a taxa de cupom.

Valor líquido = $1.000 x (96/100)
Valor líquido = $960

Custo da dívida antes dos impostos, kd.

$960 –[$75/(1 + kd)1+$75/(1 + kd)2+.....+$1.075/(1 + kd)5] =$0

Operando o custo da dívida antes dos impostos via HP 12C

960 g CF0
75 CHS g CFJ
4 g NJ
1075 CHS g CFJ
f IRR
No visor da máquina teremos 8,515473780
Portanto: kd =8,52% ao ano

Portanto, diante de um DFC onde o pagamento dos juros será anual e no último ano teremos principal mais o juro daquele ano, o custo da dívida antes dos impostos em relação à taxa de cupom, será decidido pelo valor na data focal zero.

Tela 55
Módulo 01 – Conceito de Custo de Capital

8) Com base nas seguintes informações sobre a Empresa Alpha S/A, descubra seu custo médio ponderado de capital, bem como, utilizando-se o custo de capital como taxa de corte, de que maneira novos projetos de investimentos teriam condições de ser analisados nessa empresa? Suponha que o custo de capital da empresa esteja maior que a mediana do setor, isso torna a Empresa Alpha menos competitiva, o que você recomendaria para a administração da empresa para tornar a mesma mais competitiva em termos de CMPC?

Dívida: 4.000 obrigações com cupom de 8,5% ao ano, valor de face de $1.000,00, pagamento de juros anuais, prazo da operação de cinco anos, sendo que o principal deverá ser pago no final da operação; as obrigações estão cotadas a 97,70% de seu valor nominal. A alíquota do IR/CS da empresa é de 34,0%.

Ações ordinárias: 73.000 ações, vendidas a $50 cada; seu beta é de 1,25; o prêmio pelo risco de mercado é igual a 5,5% e a taxa livre de risco é de 10,0%. O dividendo por ação pago mais recentemente foi de $4,95, e espera-se que os dividendos cresçam a uma taxa de 5,5% ao ano indefinidamente.

Ações preferenciais: 30.000 ações cotadas a $48, com dividendos de 13,0%.

Resolução

E como poderíamos melhorar (reduzir) o custo de capital da Empresa Alpha S/A? Olhando-se apenas para o cálculo matemático, podemos aumentar o peso da dívida – porque é a fonte mais barata – e reduzir (por meio da compra de ações por parte da própria empresa, por exemplo) o peso das ações ordinárias. Vamos aumentar o peso da dívida para 50% e reduzir o peso das ações ordinárias para 34%:

Ka = (ki x wi) + (kp x wP) + (ks x ws)
Ka = (6,0 x 0,50) + (13 x 0,16 ) + (16,41 x 0,34)
Ka = 10,66% ao ano

Tela 56
Unidade 01 - Matemática Básica

a) Vamos começar pelos pesos das fontes de dinheiro de longo prazo.

Valor da dívida = 4.000 x $1.000 x (97,70/100)
Valor da dívida = $3.908.000

Valor das ações preferenciais = 30.000 x $48
Valor das ações preferenciais = $1.440.000

Valor das ações ordinárias = 73.000 x $50
Valor das ações ordinárias = $3.650.000

Agora vamos operar o valor do capital total:

Capital total = $3.908.000 + $1.440.000 + $3.650.000
Capital total = $8.998.000

De posse do valor de cada fonte individual e do capital total vamos para os pesos das fontes de dinheiro de longo prazo:

wi = 3.908/8.998
wi = 0,43 ou 43%
wP = 1.440/8.998
wP = 0,16 ou 16%
wS = 3.650/8.998
wS = 0,41 ou 41%

b) Operar o custo da ação preferencial

kp = 13% (fornecido no exercício)

c) Operar o custo da ação ordinária. Nesse exercício teremos que operar o custo da ação ordinária utilizando os dois modelos: CAPM e o modelo de Gordon, caso o valor encontrado não seja o mesmo, será necessário operar o custo médio entre os dois modelos.

Tela 57
Unidade 01 - Matemática Básica

Modelo de Gordon:

Ks = (D1/P0) + g
Ks = [$4,95 (1 + 0,055)/$50] + 0,055
Ks = 15,94%

Modelo de precificação de ativos de capital (CAPM):

Ks = RF + [ß (KM – RF)]
Ks = 10 + (1,25 x 5,5)
Ks = 16,875%

Custo médio da ação ordinária:

Ks médio = (15,94+ 16,875)/2
Ks médio = 16,41%

d) Operar o custo da dívida

Valor líquido = $1000 x (97,70/100)
Valor líquido = $977

Juros anuais = $1.000 x (8,5/100)
Juros anuais = $85


Valor a ser pago no Ano 5 = $1.000 + $85
Valor a ser pago no Ano 5 = $1.085

DFC da dívida

Tela 58
Unidade 01 - Matemática Básica

Custo da dívida antes dos impostos, kd.

$977 –[$85/(1 + kd)1+$85/(1 + kd)2+.....+$1.085/(1 + kd)5] =$0

Observe, o valor inicial é menor que o valor de face ($977 < $1.000) enquanto que os juros foram operados sobre o valor de face, isso significa que o custo nominal para a empresa será maior que a taxa de cupom.

Operando o custo da dívida antes dos impostos via HP 12C

977 g CF0
85 CHS g CFJ
4 g NJ
1085 CHS g CFJ
f IRR
No visor da máquina teremos 9,092736151
Portanto: kd = 9,09% ao ano

Vamos operar o custo da dívida depois dos impostos:

Ki = kd (1 – T)
Ki = 9,09 (1 – 0,34)
Ki = 6,0%

e) Agora, estamos em condições de operar o CMPC da empresa, pois, já dispomos dos pesos e do custo de cada fonte de dinheiro de longo prazo.

Ka = (ki x wi) + (kp x wP) + (ks x ws)
Ka = (6,0 x 0,43) + (13 x 0,16 ) + (16,41 x 0,41)
Ka = 11,39% ao ano

Novos projetos de investimento deverão apresentar taxa de retorno > 11,39%, com isso será possível alcançar VPL >$0 e atender ao objetivo de uma empresa em finanças corporativas: a maximização da riqueza do(s) proprietário(s).

Tela 59
Módulo 01 – Conceito de Custo de Capital

A situação melhorou um pouco, pois agora a empresa poderá tocar projetos não mais com IRR >11,39%, mas sim com IRR >10,66%. Ocorre que a alteração dos pesos poderia ser vista de outra maneira pelo mercado. Os investidores poderiam enxergar aumento do risco de crédito da empresa, pois o aumento do peso da dívida irá exigir mais fluxo de caixa para o pagamento do serviço da dívida. Isso poderia vir a prejudicar a empresa ao invés de ajudar, portanto, mudanças baseadas em alterações nos pesos das fontes tendo como pano de fundo o custo das fontes é muito perigoso.

O melhor caminho será a empresa tratar de administrar melhor os seus ativos procurando encontrar uma estrutura de capital ótima para o seu negócio. Por exemplo, nada de ficar expondo as sobras de caixa da empresa em aplicações financeiras fora da realidade. O melhor a fazer é adotar uma política de crédito conservadora e operar instrumentos que permitam uma administração de estoques eficiente. No parque fabril, é importante não deixar os equipamentos virarem sucata; políticas de manutenção dos equipamentos acompanhadas de muito treinamento da mão-de-obra deverão fazer parte do dia a dia da empresa etc.


Tela 60
Módulo 01 – Conceito de Custo de Capital

Na administração do passivo exigível todo cuidado deve ser observado com a captação de dinheiro, ou seja, saber escolher as instituições financeiras que melhor atendam as necessidades da empresa.

Por exemplo, suponha que a empresa tenha facilidade de colocar seus produtos na Ásia, nesse caso, seria interessante que uma das instituições financeiras da empresa fosse um banco com forte penetração na Ásia. Se a empresa está num segmento com potencial de grande crescimento, se faz necessária uma aproximação com bancos que tenham forte atuação com produtos do BNDES etc.

O que fazer caso a empresa não consiga gerar projetos de investimento com IRR maior que a taxa de corte? Segundo Damodaran (2004, p. 608):


“Se não há investimentos suficientes que cubram a taxa de corte, deve-se devolver recursos aos proprietários da empresa. A forma das devoluções – dividendos e recompra de ações – dependerá das características dos acionistas”.

Tela 61
Módulo 01 – Conceito de Custo de Capital

Resumo

O custo médio ponderado de capital (CMPC) ou custo de capital reflete a política de utilização de dinheiro adotada pela administração de uma empresa. Três são as fontes de longo prazo mais utilizadas pelas empresas: ações ordinárias, ações preferenciais e dívida. Em sociedades por ações uma dessas fontes estará sempre presente na estrutura de capital da empresa: a ação ordinária.

Além do custo individual de cada fonte, será necessário que seja apurado o peso de cada fonte de dinheiro empregado pela empresa. Os pesos poderão ser calculados com base no valor contábil ou no valor de mercado e poderão ser usadas proporções históricas ou ideais.

O custo de capital será afetado por uma variedade de fatores. Alguns estarão além do controle da empresa, enquanto outros serão influenciados pelas políticas de financiamento e de investimento adotadas pela administração da empresa.