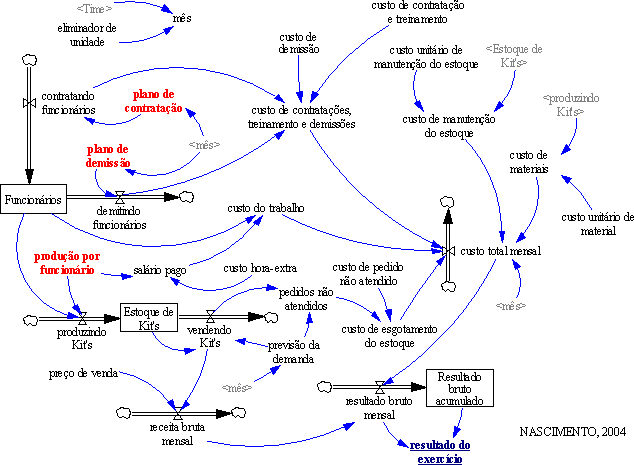
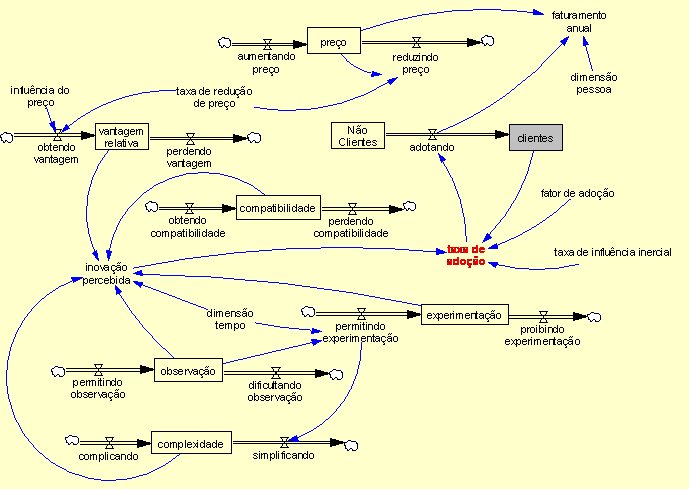
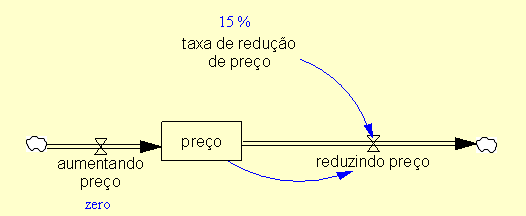
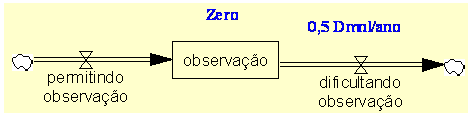
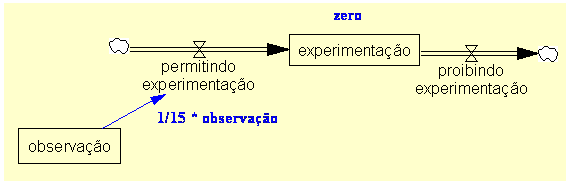
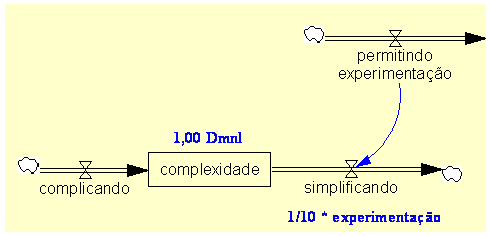
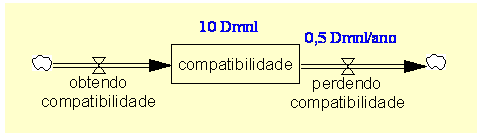
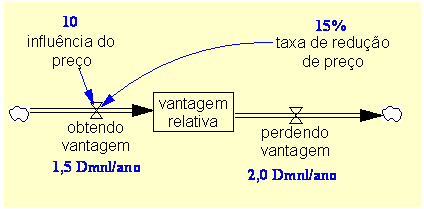
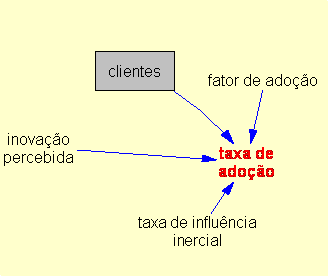
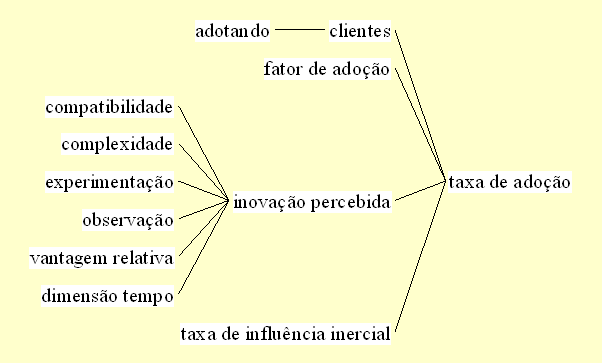
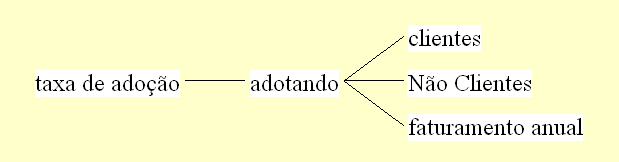
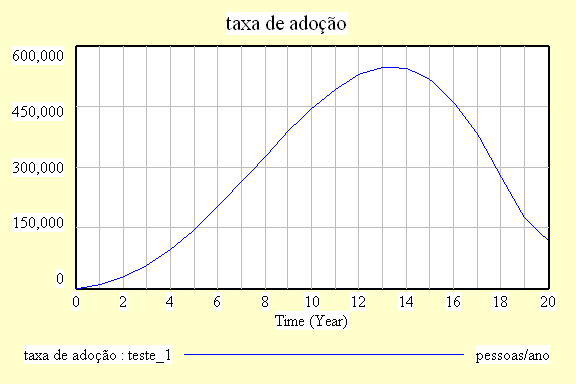
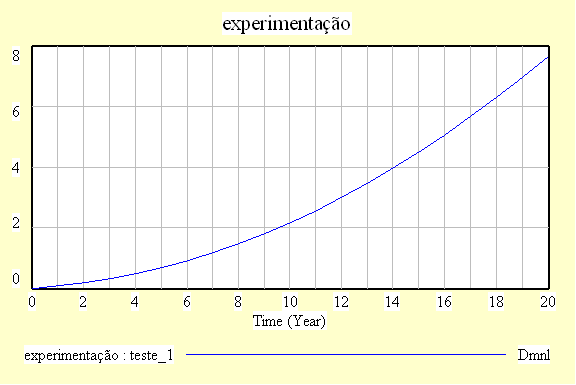
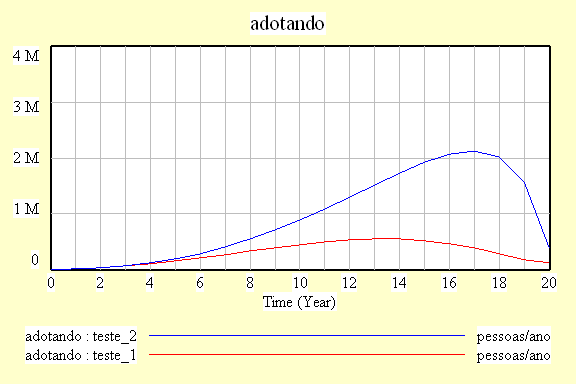
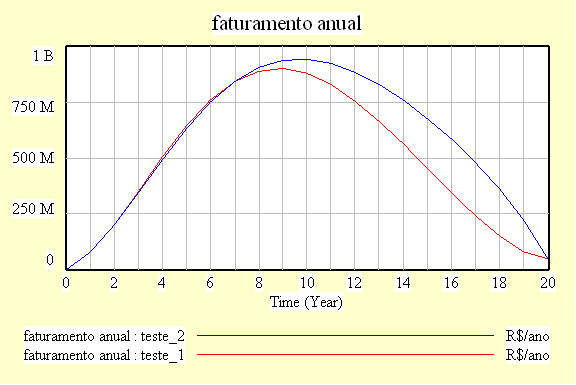
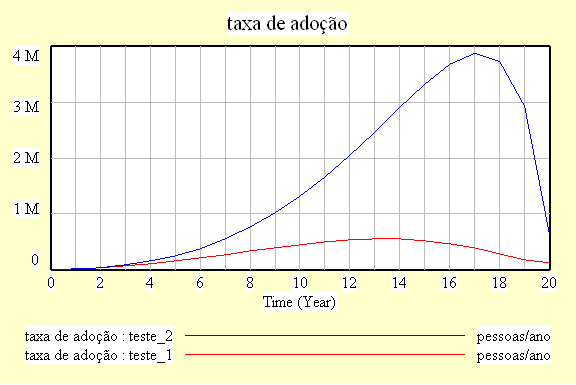
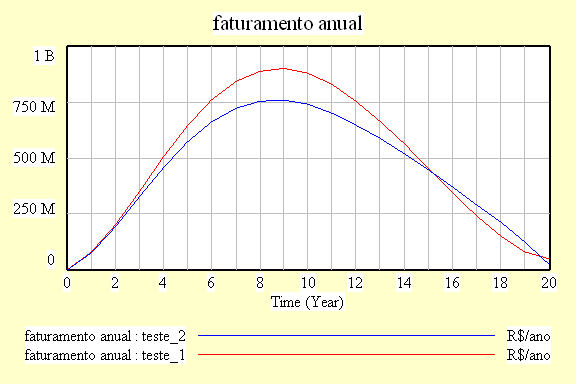
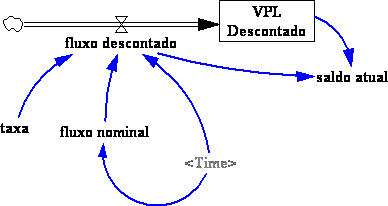
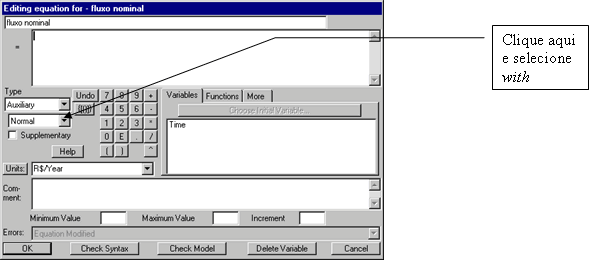
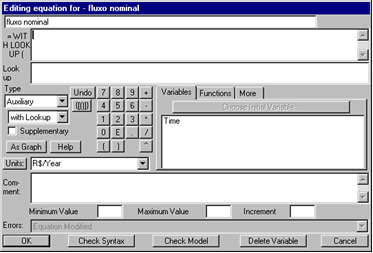
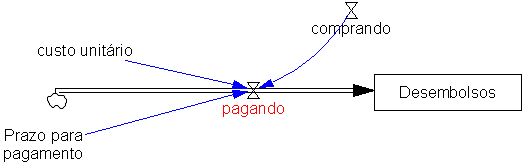
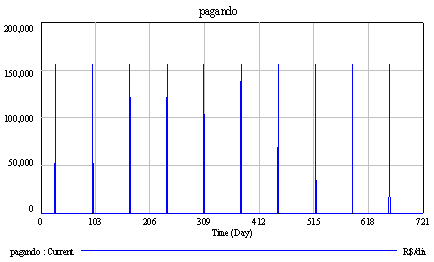
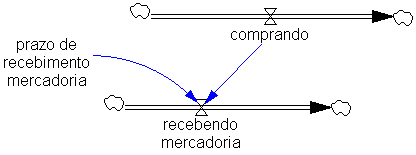
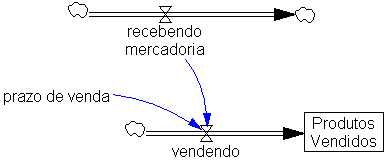
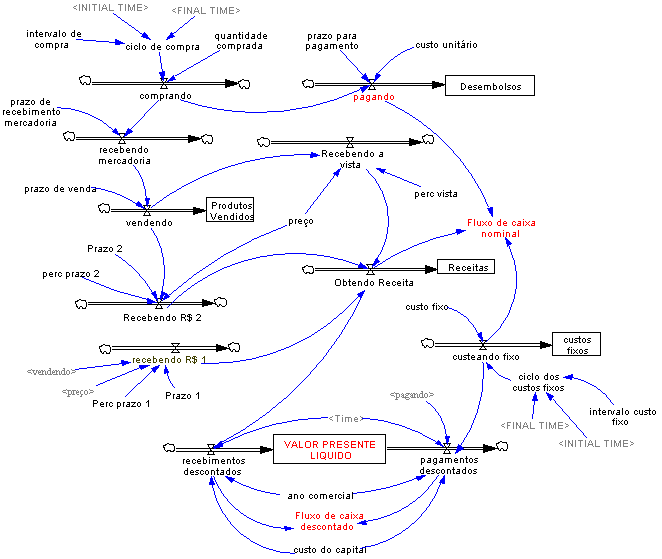
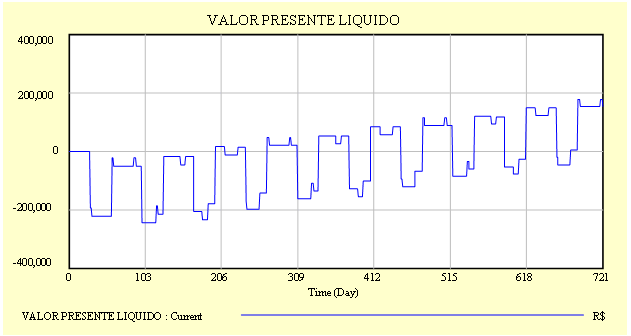
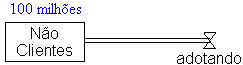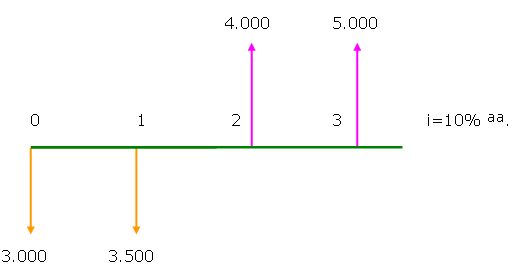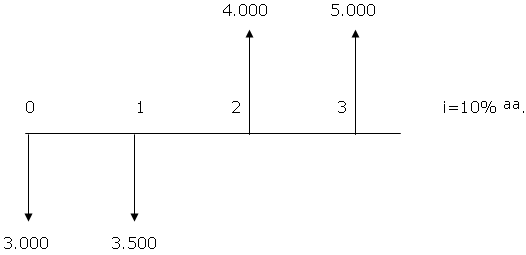| Diagrama
do modelo
| (01) |
contratando
funcionários=plano de contratação
Units: funcionários/mês |
| (02) |
custo
de contratação e treinamento=300
Units: R$/funcionário |
| (03) |
"custo
de contratações, treinamento e demissões"=(contratando
funcionários*custo de contratação e treinamento)+(demitindo
funcionários*custo de demissão)
Units: R$/mês |
| (04) |
custo
de demissão=500
Units: R$/funcionário |
| (05) |
custo
de esgotamento do estoque=custo de pedido não atendido*pedidos
não atendidos
Units: R$/mês |
| (06) |
custo
de manutenção do estoque=Estoque de Kit's*custo unitário
de manutenção do estoque
Units: R$/mês |
| (07) |
custo
de materiais=produzindo Kit's*custo unitário de material
Units: R$/mês |
| (08) |
custo
de pedido não atendido=5
Units: R$/Kit |
| (09) |
custo
do trabalho=Funcionários*salário pago
Units: R$/mês |
| (10) |
"custo
hora-extra"=21.6
Units: R$/Kit |
| (11) |
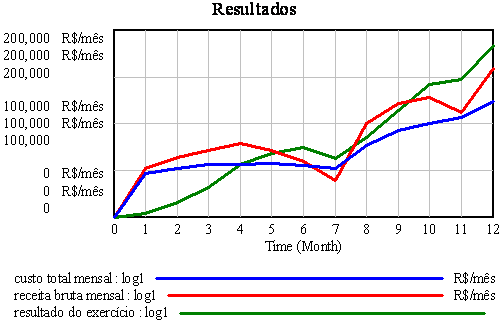
custo
total mensal=IF THEN ELSE (mês>0,"custo de contratações,
treinamento e demissões"+custo de esgotamento do estoque+custo
de manutenção do estoque+custo de materiais+custo do
trabalho,0)
Units: R$/mês |
| (12) |
custo
unitário de manutenção do estoque=2
Units: R$/Kit/mês |
| (13) |
custo
unitário de material=10
Units: R$/Kit |
| (14) |
demitindo
funcionários=plano de demissão
Units: funcionários/mês |
| (15) |
eliminador
de unidade=1
Units: mês |
| (16) |
Estoque
de Kit's= INTEG (produzindo Kit's-vendendo Kit's,100)
Units: kits |
| (17) |
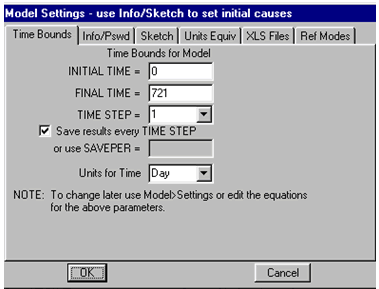
FINAL
TIME = 12
Units:
Month
The final time for the simulation. |
| (18) |
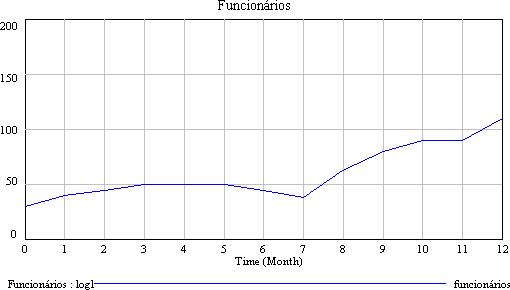
Funcionários=
INTEG (contratando funcionários–demitindo funcionários,30)
Units: funcionários |
| (19) |
INITIAL
TIME = 0
Units: Month
The initial time for the simulation. |
| (20) |
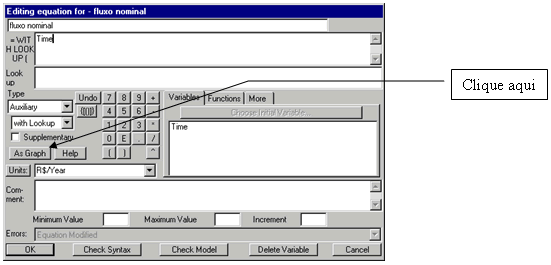
mês=
Time/eliminador de unidade
Units: Dmnl
mês assume os valores dos meses, representados
pela variável <time> do Vensim. Como essa variável
é utilizada na função lookup, o Vensim gera uma
mensagem de erro de unidade. Para eliminar essa mensagem, cria-se
a variável mês dividindo time pelo eliminador de unidade. |
| (21) |
pedidos
não atendidos=previsão da demanda-vendendo Kit's
Units: kits/mês |
| (22) |
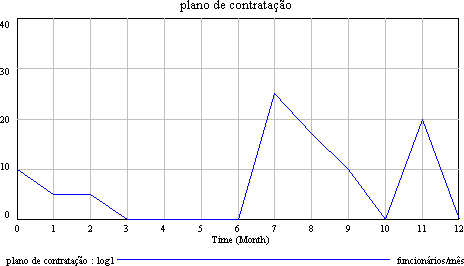
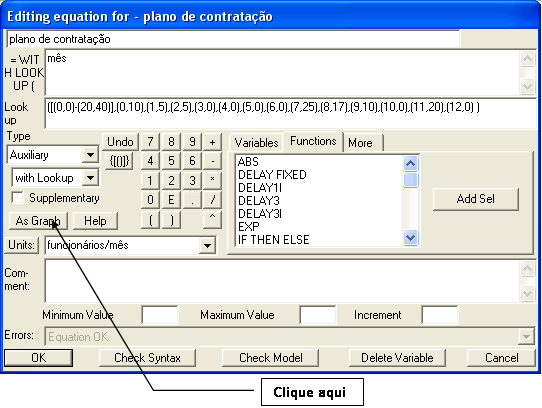
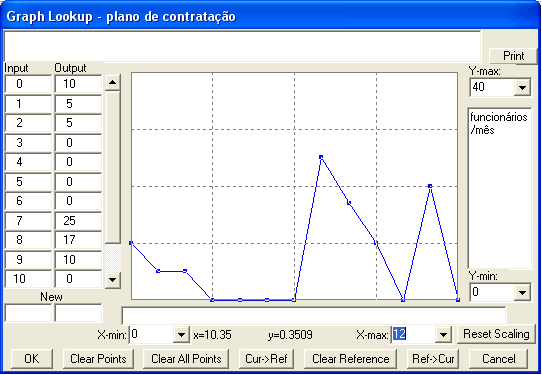
plano
de contratação = WITH LOOKUP (mês,([(0,0)-(20,40)],(0,10),(1,5),(2,5),(3,0),(4,0),(5,0),(6,0),(7,25),(8,17),(9,10),(10,0),
(11,20),(12,0) ))
Units: funcionários/mês |
| (23) |
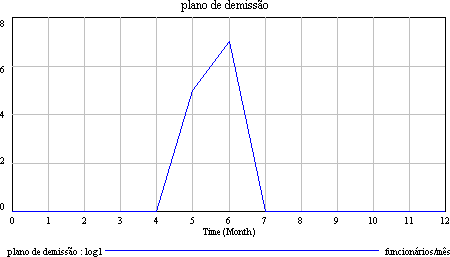
plano
de demissão = WITH LOOKUP (mês,([(0,0)-(20,10)],(0,0),(1,0),(2,0),(3,0),(4,0),(5,5),(6,7),(7,0),(8,0),(9,0),(10,0),
(11,0),(12,0) ))
Units: funcionários/mês |
| (24) |
preço
de venda=40
Units: R$/Kit |
| (25) |
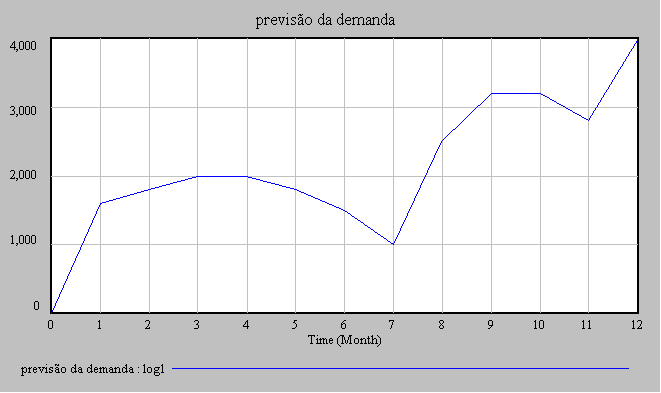
previsão
da demanda = WITH LOOKUP (mês,([(0,0)-(12,4000),(0,0),(1,1600),
(2,1800),(3,2000),(4,2000),(5,1800),(6,1500),(7,1000),(8,2500),(9,3200),
(10,3200),(11,2800),(12,4000),(13,0)],(0,0),(1,1600),(2,1800),(3,2000),
(4,2000),(5,1800),(6,1500),(7,1000),(8,2500),(9,3200),(10,3200),
(11,2800),
(12,4000) ))
Units: kits/mês |
| (26) |
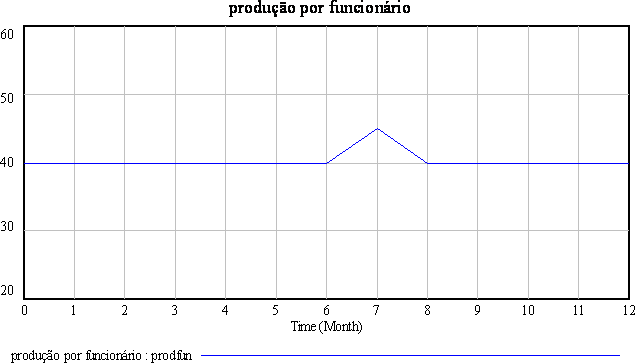
produção
por funcionário=40
Units: kits/mês/funcionário |
| ( 27) |
produzindo
Kit's=Funcionários*produção por funcionário
Units: kits/mês |
| (28) |
receita
bruta mensal=preço de venda*vendendo Kit's
Units: R$/mês |
| (29) |
Resultado
bruto acumulado= INTEG (resultado bruto mensal, 0)
Units: R$ |
| (30) |
resultado
bruto mensal=receita bruta mensal-custo total mensal
Units: R$/mês |
| (31) |
resultado
do exercício=Resultado bruto acumulado+resultado bruto mensal
Units: R$ |
| (32) |
salário
pago=640+((produção por funcionário-40)*"custo
hora-extra")
Units: R$/mês/funcionário |
| (33) |
SAVEPER=TIME
STEP
Units: Month [0,?]
The frequency with which output is stored. |
| (34) |
TIME
STEP = 1
Units:
Month [0,?]
The time step for the simulation. |
| (35) |
vendendo
Kit's=IF THEN ELSE (Estoque de Kit's>=previsão da demanda,
previsão da demanda, Estoque de Kit's)
Units: kits/mês |
Você
agora está em um micromundo gerencial. Que tenha um ótimo
desempenho!
|