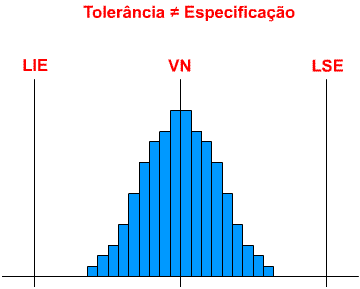
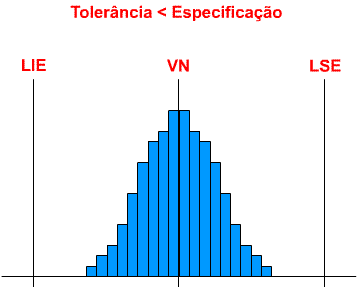
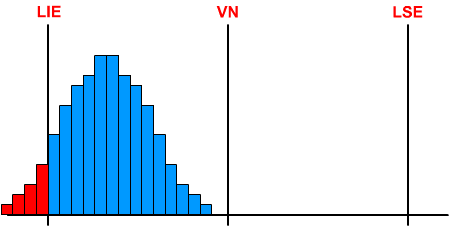
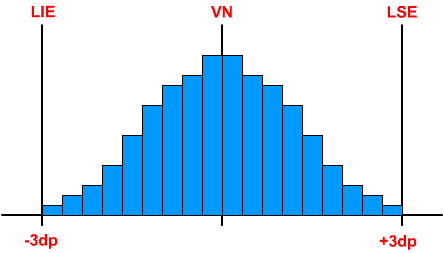
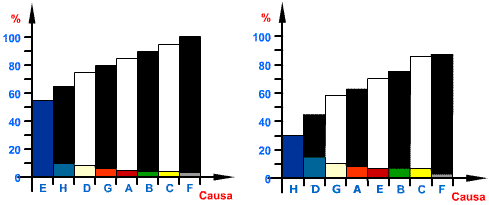
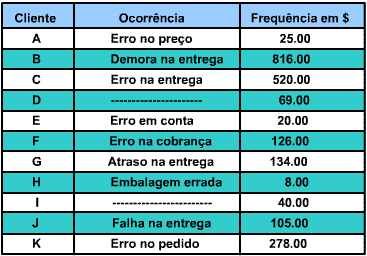
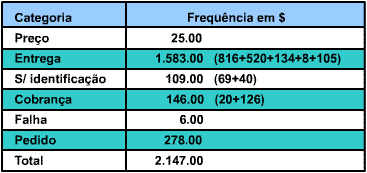
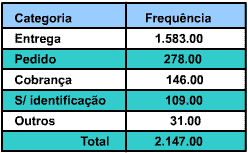
Resumo
Causas especiais podem atuar sobre um processo, deixá-lo fora de
controle leva a diferenças nos resultados. A significância
das diferenças deve, muitas vezes, ser avaliada com o auxílio
de técnicas estatísticas. Essas causas são descritas
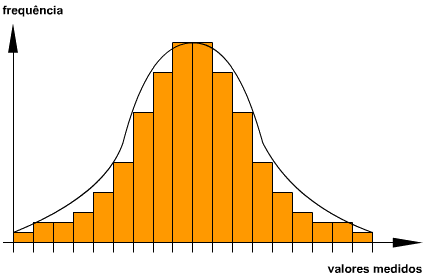
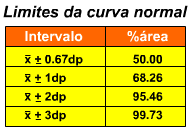
com base na distribuição normal de frequência, que
constitui a base do critério estatístico.
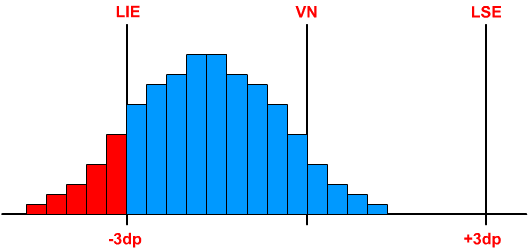
Uma variação
anormal ocorre quando o desempenho fica fora dos limites inferiores e
superiores do gráfico de controle. Este tipo de variação
não pode ser previsto, pois ela acontece em virtude de causas especiais.
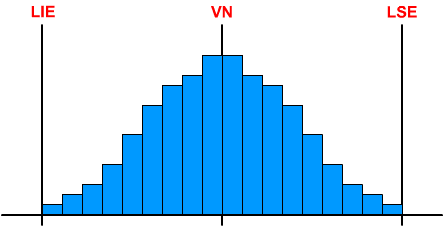
Uma variação
normal é a flutuação no desempenho de rotina graças
à existência de certa quantidade de causas comuns. No decorrer
de um determinado tempo, os dados indicadores do processo podem aumentar
ou diminuir, mas é possível predizer, com grau razoável
de certeza, qual será a faixa de variação.
As causas especiais,
que ocasionam variações anormais, são responsáveis
por apenas, em média, 15% do nível de variação
do processo. As causas comuns, responsáveis pelas variações
normais, são responsáveis pelos restantes 85%.
Quando se remove uma
causa especial de variação anormal, o processo está
sendo consertado, isto é, o processo volta a funcionar normalmente.
Quando se elimina ou reduz a intensidade de uma causa comum, o processo
é melhorado.
Para se melhorar um
processo é necessário torná-lo estável. Mas,
um processo estável pode não atender ao cliente. Para atendê-lo
são necessárias melhorias no processo, isto é, reduzir
a variação normal.
O Controle Estatístico
de Processo (CEP) se baseia no uso de Gráficos de Controle. Eles
permitem que o processo "fale" com os operadores, eles ajudam
a manter o processo sob controle por meio dos gráficos de controle
de variáveis: Gráfico da Média e Gráfico da
Amplitude.
|