Módulo 1

Página 1
Módulo 03 - Modelo da Equipe de Trabalho e Estoque
1 - Modelo Dinâmico de Simulações - Pressupostos

Serão focalizadas determinadas características, análises e uso de um modelo organizacional. Depois de estudá-lo, terá uma compreensão muito melhor de como pensar e trabalhar um modelo dinâmico por meio de simulações com o Vensim. A partir de agora, não haverá instruções passo a passo, exceto se houver necessidade. Caso tenha dificuldade, deverá consultar os conteúdos de Modelagem e Simulação de Negócios I para dirimir dúvidas.

Suponha uma determinada empresa que é envolvida na produção e venda de perfis para janelas. Embora a empresa esteja indo bem, atravessa alguns períodos em que a produção trabalha muito abaixo de sua capacidade e outros em que precisaria operar acima de seus limites. Normalmente, coloca-se a culpa na demanda do mercado e na economia por essas oscilações, no entanto, o dono da empresa tem suas dúvidas. Analisando as vendas e a produção dos últimos oito anos, lhe pareceu que as vendas são mais estáveis que a produção. Ele decide, então, identificar o problema e procurar alguma solução.


UPIS | EAD

Página 2
Módulo 03 - Modelo da Equipe de Trabalho e Estoque
Para abordar esse problema, ele decide simplificar, na medida do possível, a dimensão do modelo, pelas seguintes razões:
  • É mais fácil compreender um modelo simples.
  • É possível obter resultados mais rapidamente.
  • É mais eficiente iniciar com um modelo simples e ir adicionando detalhes do que construir um modelo complexo para depois analisá-lo.
  • Usar um modelo simples força a ter uma visão geral do problema o que é particularmente interessante nas fases iniciais de modelagem.

Porém, não é sempre que devemos começar com modelos simples. Em muitos casos, o problema pode ser resultado da própria complexidade e, nesse caso, será necessário construir um modelo mais complexo. Contudo, até que se adquira experiência, é melhor trabalhar com modelos simples. Não é incomum descobrir que um determinado modelo não é rico o suficiente para lidar com um problema, mas é raro não aprender e adquirir novos conhecimentos com o processo.

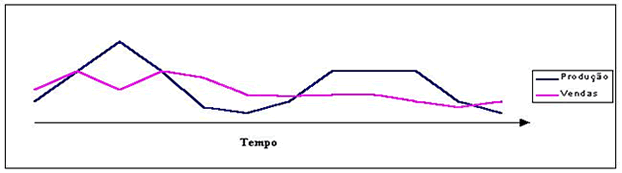
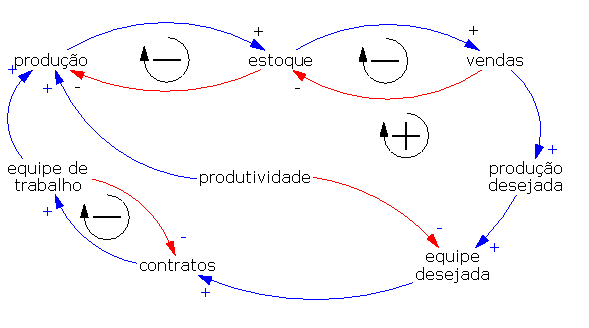
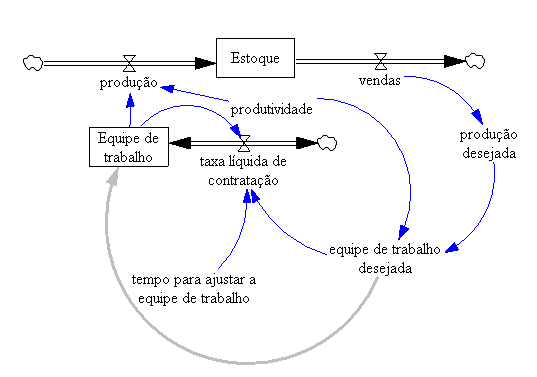
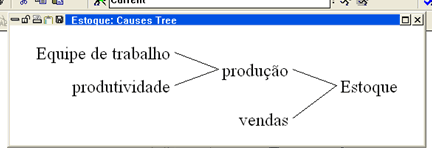
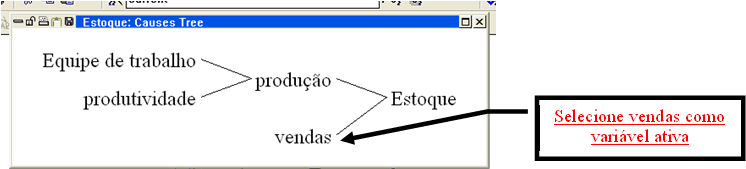
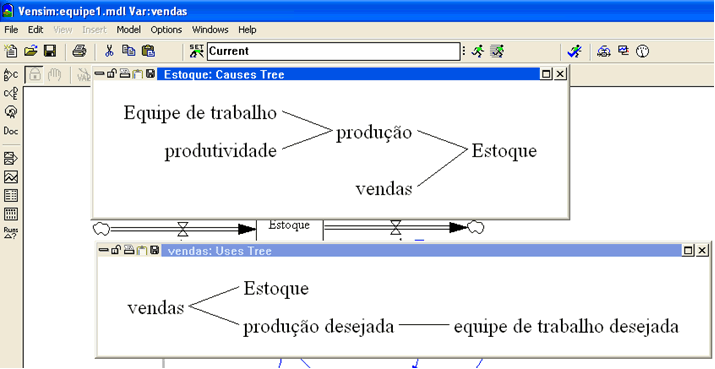
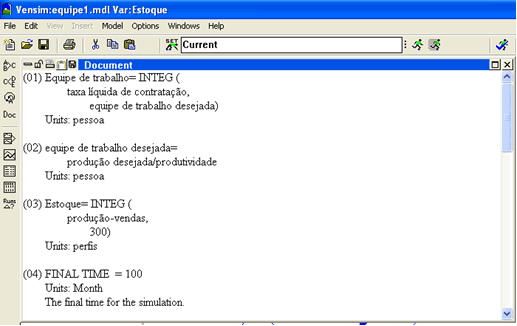
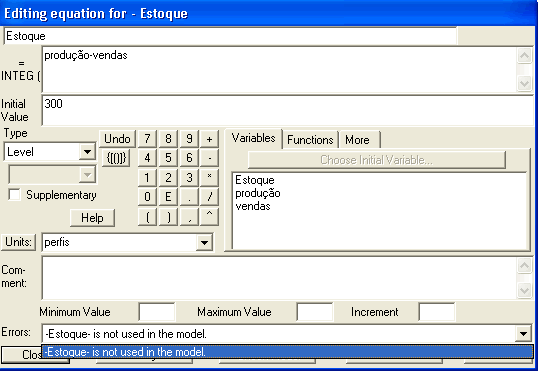
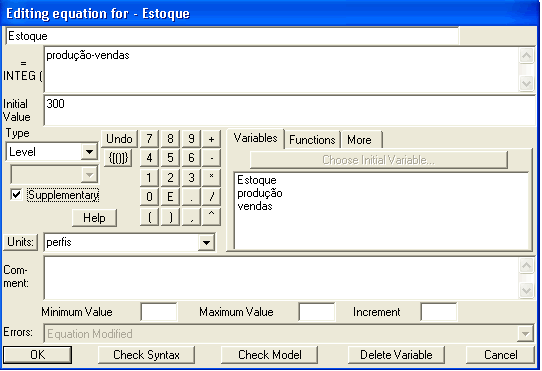
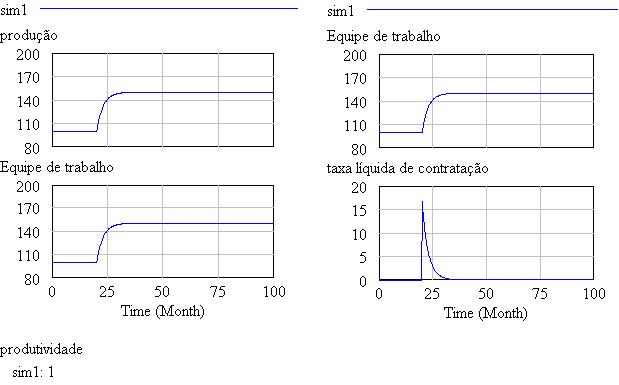
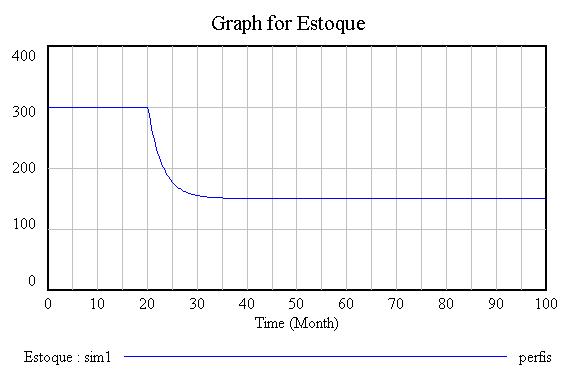
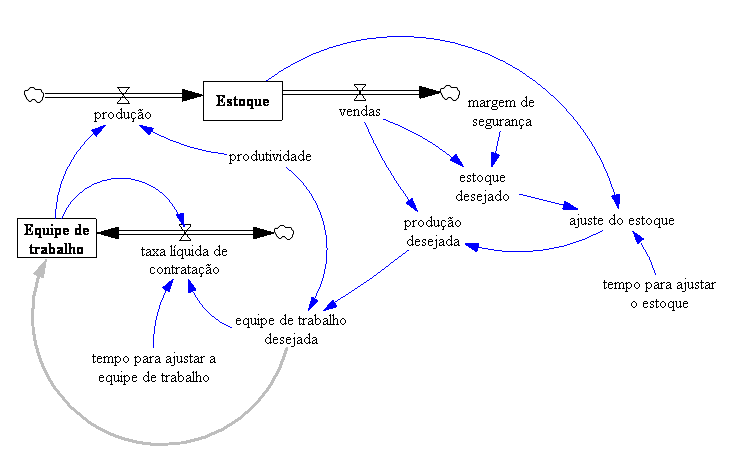
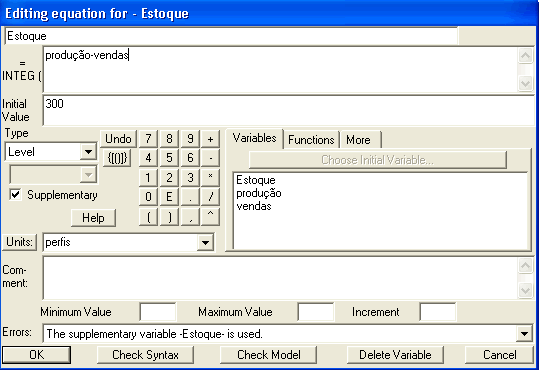
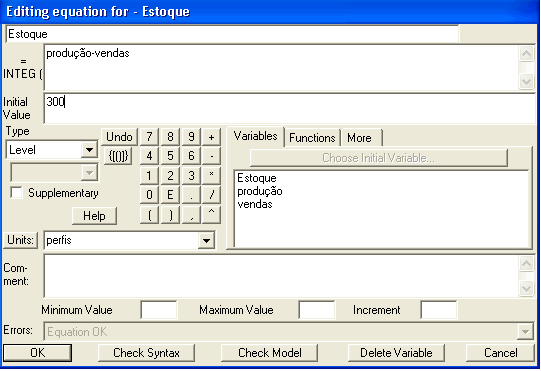
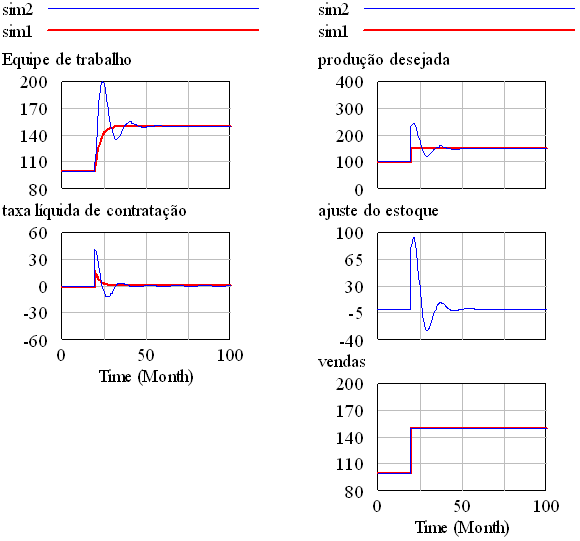
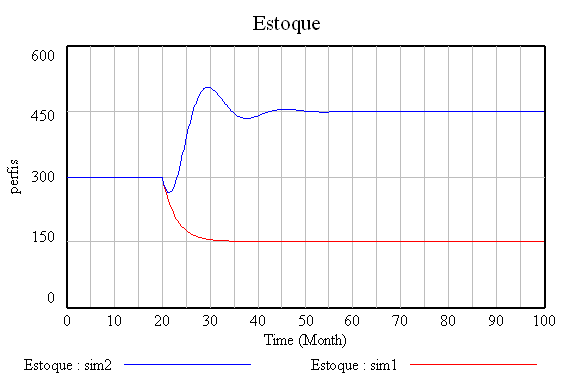
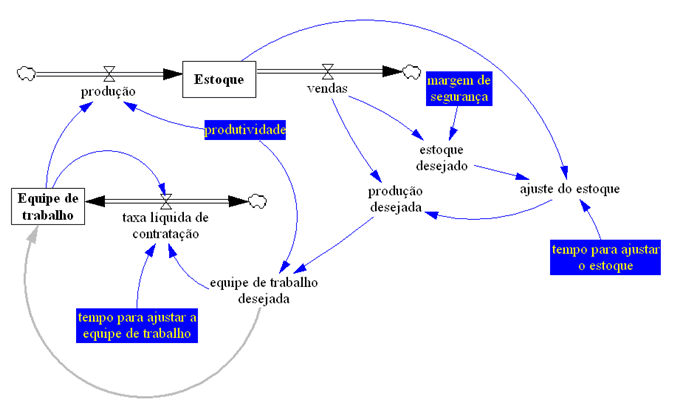
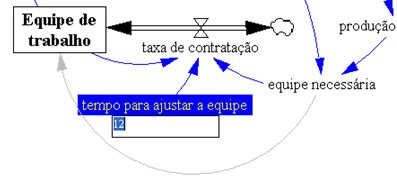
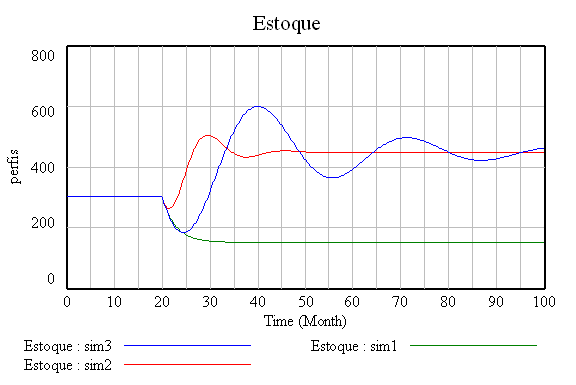
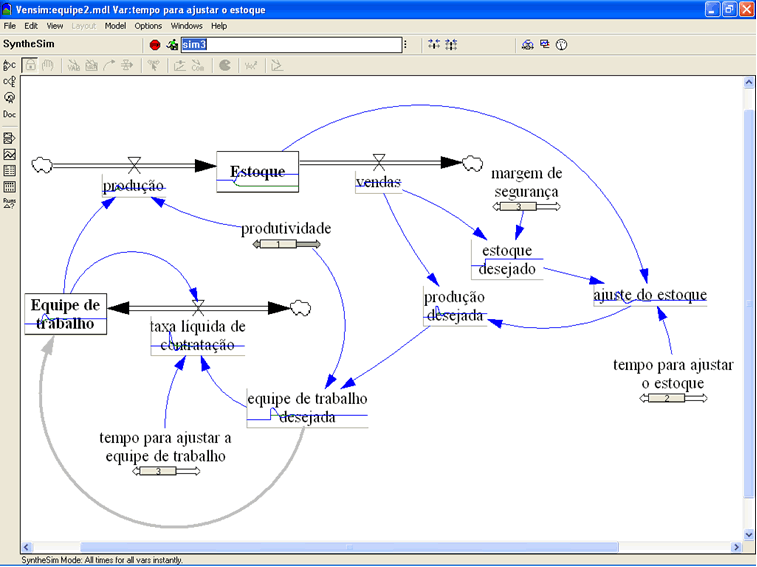
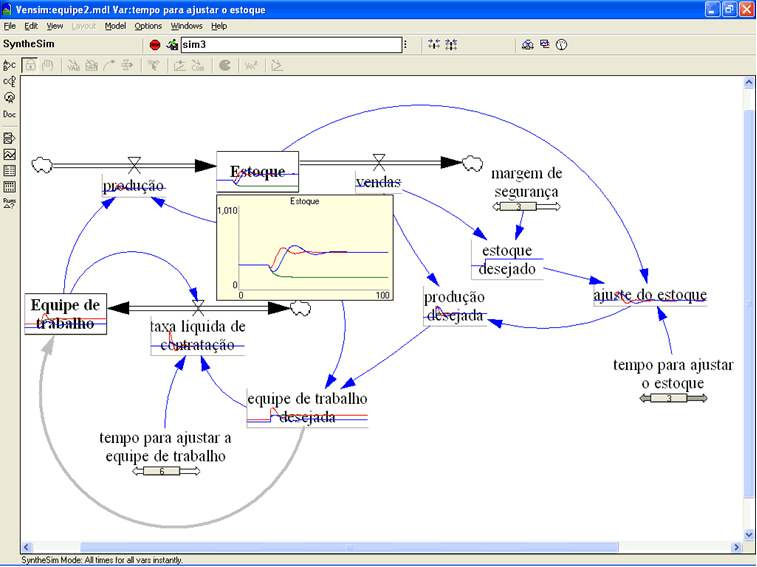
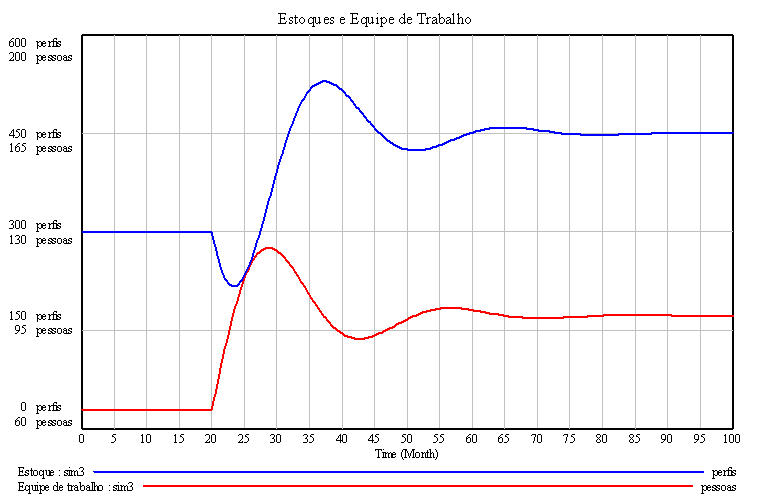
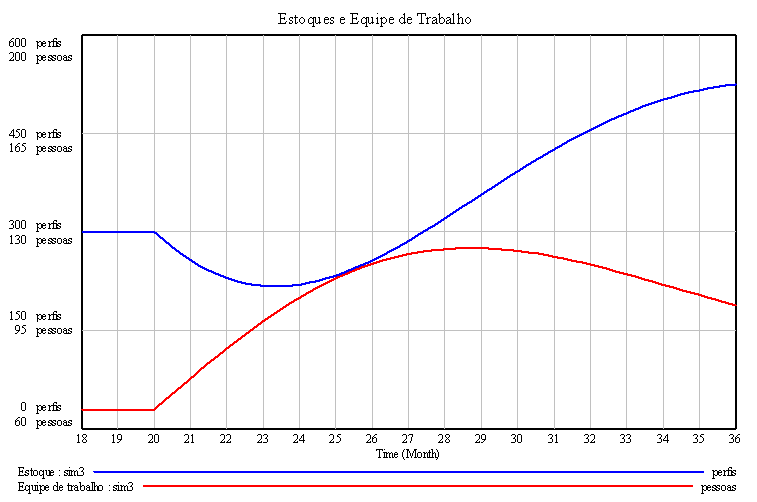
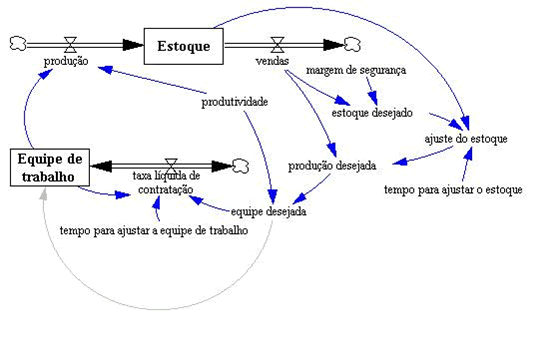
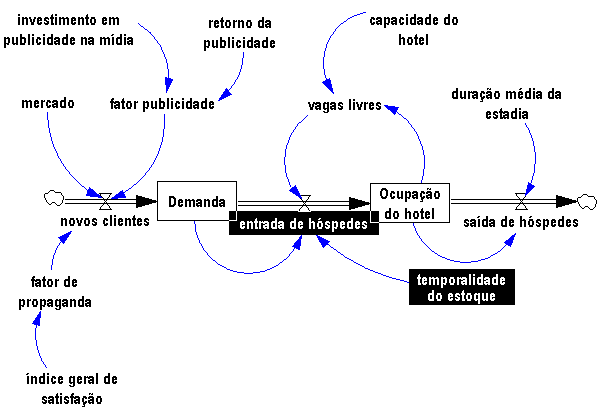
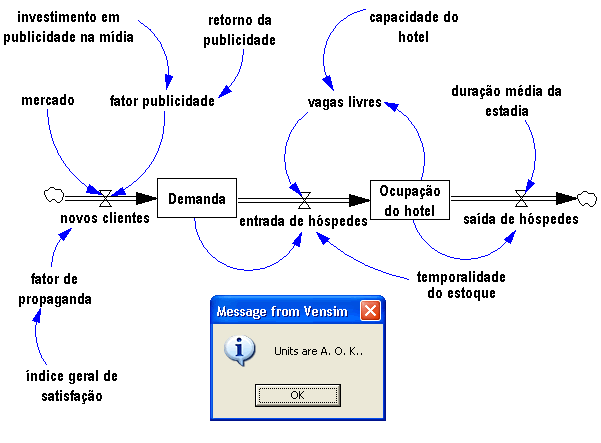
Coerente com qualquer realidade administrativa, o estoque é determinado pela produção (aumento do estoque) e pelas vendas (redução do estoque). Completando o diagrama, excesso de estoque reduz a produção e promove as vendas. Portanto o estoque é regulado por dois feedbacks negativos.


UPIS | EAD

Página 3
Módulo 03 - Modelo da Equipe de Trabalho e Estoque
Outro modelo referencial pode ser obtido com uma visão gráfica do problema. Dissemos que "a produção é menos estável do que as vendas", o que pode ser observado no histórico de 8 anos da empresa, detalhado no gráfico a seguir:

Esse modelo referencial é um rascunho do comportamento que esperamos que o modelo venha a produzir. Ele é utilizado para focar nossa atividade. Uma vez que tenhamos analisado um ou mais desses modelos, o objetivo passa a ser a definição de uma estrutura simples e capaz de gerar padrões de comportamento próximos aos modelos referenciais. Se necessário, pode-se, por exemplo, construir um modelo que possa ser validado quantitativamente contra dados reais.


UPIS | EAD

Página 4
Módulo 03 - Modelo da Equipe de Trabalho e Estoque
Uma hipótese dinâmica é uma idéia sobre que tipo de estrutura pode ser capaz de gerar um comportamento semelhante aos modelos de referência. No exemplo utilizado, podemos formular a hipótese dinâmica pensando sobre como as duas variáveis do modelo de referência estão relacionadas, ou seja, que regras determinam produção e vendas.

A hipótese dinâmica para essa empresa é a de que o gerente estabelece a produção com base nas vendas, porém sempre aumenta (ou diminui) um pouco a quantidade de modo que algumas vezes se produz mais (ou menos) do que seria necessário.

O modelo de referência nos fornece duas variáveis - produção e vendas - que iremos utilizar. Essa já é uma boa base para iniciarmos a construção de nosso modelo.


UPIS | EAD

Página 5
Módulo 03 - Modelo da Equipe de Trabalho e Estoque
2 - Construindo o Modelo
  • Inicie o Vensim e clique no botão New Model ou excute o comando File>New Model.
  • Estabeleça os parâmetros na caixa de diálogo Time Bounds como:
    • INITIAL TIME = 0
    • FINAL TIME = 100
    • TIME STEP = 0.25
    • Units for time = Month

    • Dê um clique na guia Units Equiv (Unidades equivalentes). Selecione com o mouse a linha em que está escrito Person,People,Persons e clique no botão Modify Selected.
    • Na caixa de edição, digite uma vírgula e complete com Pessoa,Pessoas.
    • Dê um clique no botão Make these synonyms the New Model default synonyms, confirme a mudança nas equivalências (Do you want to replace default units equivalences?) e OK para fechar a janela do Model Settings. Isso fará com que essas unidades fiquem disponíveis para os novos modelos que forem criados.
    • Agora, para o Vensim, Person,People,Persons, Pessoa,Pessoas significam a mesma coisa.
    • Abra novamente as configurações do modelo (Model Settings) e acesse a guia Units Equiv. Dê um clique no botão Replace these with the New Model default synonyms, para recuperar os sinônimos cadastrados, inclusive a alteração realizada anteriormente.

    • Salve o modelo como equipe1.mdl.

Antes de adicionar as variáveis produção e vendas ao modelo, devemos perguntar como estão relacionadas. Está claro que guardam um relacionamento muito próximo, já que é necessário produzir alguma coisa para poder vendê-la. Na verdade, produção e vendas se relacionam de duas formas:

  1. Física: a produção é necessária para criar as mercadorias a serem vendidas;
  2. Informacional: os gerentes baseiam a produção nas vendas atuais ou recentes.


UPIS | EAD

Página 6
Módulo 03 - Modelo da Equipe de Trabalho e Estoque
Vamos iniciar o modelo do ponto de vista físico. As indústrias, de modo geral, trabalham de duas formas: ou produzem sob encomenda ou produzem para venda posterior. Nos dois casos, utiliza-se um estoque de produtos acabados, porém, se fôssemos modelar a produção sob encomenda, deveríamos considerar as ordens de produção e os embarques para distribuição. No nosso exemplo, vamos considerar a venda posterior.

Vamos construir o Estoque como uma variável Level (estoque) e adicionar os fluxos de entrada e saída, ou seja, produção e vendas, respectivamente.

Dúvidas sobre diagramação de fluxos e estoques?



Uma vez que se consiga reconhecer os padrões desses sistemas, obtém-se entendimento mais profundo sobre eles (...) As estruturas determinam o comportamento dos sistemas de modos notavelmente semelhantes. Pode-se, além disso, pensar em termos mais amplos sobre suas implicações. Passa-se a ver a "floresta", assim como as "árvores", os inter-relacionamentos entre os elementos do sistema ficam mais visíveis.
Verifique como os comportamentos dos modelos simulados na disciplina de modelagem I assemelham-se ao comportamento do modelo equipe1:

“Estoque” está para “População” assim como “produção” está para “nascimentos” e “vendas” está para “mortes” do Estoque.


UPIS | EAD

Página 7
Módulo 03 - Modelo da Equipe de Trabalho e Estoque
3 - Equipe de Trabalho

Agora, necessitamos representar como a produção é determinada. No longo prazo, investimentos e capacidade de produção são relevantes, mas vamos considerá-los estáveis. No curto prazo, pessoas podem ser contratadas e podem ocorrer aumentos na produção. Essas mudanças, muitas vezes, podem trazer problemas como alterações nos programas de manutenção, entrosamento entre os funcionários, etc. Entretanto, como uma abordagem inicial, vamos considerar que mais pessoas produzem mais mercadorias. Nesse caso, vamos adicionar uma variável do tipo Level chamada Equipe de trabalho, que vai atuar na produção. Para construir a figura abaixo, com a seta bidirecional, siga os passos a seguir.

  • Selecione a variável Level e dê um clique logo abaixo de produção. Digite Equipe de trabalho e tecle Enter.
  • Selecione a variável Rate dê um clique no espaço em branco à direita de Equipe de trabalho. Mova o mouse para a esquerda, sem pressioná-lo, e dê um clique sobre Equipe de trabalho.Identifique o fluxo taxa líquida de contratação.


UPIS | EAD

Página 8
Módulo 03 - Modelo da Equipe de Trabalho e Estoque
Para criar a seta bidirecional, faça o seguinte:
  • Selecione a ferramenta Move/Size (o ícone da mãozinha).

  • Dê um clique no handle do fluxo que não tem seta com o botão direito do mouse, conforme figura abaixo:

  • Na caixa de diálogo que se abre, marque o quadradinho no alto à esquerda onde está escrito Arrowhead. Clique OK.


UPIS | EAD

Página 9
Módulo 03 - Modelo da Equipe de Trabalho e Estoque
4 - Relacionamentos Comportamentais

Essa é a parte física do problema, sendo necessário fazer algumas das conexões comportamentais. Construir os estoques e fluxos físicos do modelo é sempre um bom ponto de partida, pois nos leva a conhecer o sistema concretamente, simplificando a conceitualização de outras partes do sistema.

Uma excelente abordagem para identificar relacionamentos é construir, primeiramente, um diagrama de ciclos causais (sem se preocupar com estoques ou fluxos):

Posteriormente, convertemos em um diagrama de fluxos e estoques.


UPIS | EAD

Página 10
Módulo 03 - Modelo da Equipe de Trabalho e Estoque
Identificando os relacionamentos, vamos tentar manter as coisas o mais simples possível, estabelecendo que a produção é proporcional à Equipe de trabalho. Para isso, adicionamos a constante produtividade. Convém lembrar também que a taxa líquida de contratação é dependente do valor da Equipe de trabalho, ou seja, quanto maior a Equipe de trabalho menor a taxa líquida de contratação e vice-versa. Complete as conexões conforme o modelo abaixo:


UPIS | EAD

Página 11
Módulo 03 - Modelo da Equipe de Trabalho e Estoque
A taxa líquida de contratação é o número líquido de pessoas contratadas. A melhor maneira de formular isso é como um processo de ajustamento de estoque. Nesse processo, tomamos um valor de um estoque e comparamos com o nível desejado para esse estoque. Então, tomamos uma ação no sentido de diminuir a diferença entre os dois. Suponha, por exemplo, que esteja dirigindo um carro a 70 Km/h e deseje atingir 80 Km/h. Para isso, deve-se pressionar o acelerador. A velocidade do carro (o estoque) vai aumentar na taxa proporcional à pressão no acelerador e vai demorar certo tempo até atingir a velocidade desejada.


UPIS | EAD

Página 12
Módulo 03 - Modelo da Equipe de Trabalho e Estoque
Para estabelecer esse processo de ajustamento do estoque, vamos adicionar as variáveis equipe de trabalho desejada e tempo para ajustar a equipe de trabalho e conectá-las como mostrado abaixo:


UPIS | EAD

Página 13
Módulo 03 - Modelo da Equipe de Trabalho e Estoque
A variável tempo para ajustar a equipe de trabalho representa o espaço de tempo necessário para gerenciar as mudanças na equipe, como a entrada de novos funcionários (necessitam de treinamento) ou a demissão de outros (devem cumprir aviso prévio). A variável equipe de trabalho desejada é o número de trabalhadores necessário para produzir uma determinada quantidade de mercadorias desejada. A variável Equipe de trabalho é inicializada com esse valor. Agora, vamos adicionar o conceito de produção desejada e conectá-lo a variável equipe de trabalho desejada. Em seguida, vamos estabelecer a produção desejada em relação às vendas.


UPIS | EAD

Página 14
Módulo 03 - Modelo da Equipe de Trabalho e Estoque
Faça as modificações de acordo com a figura a seguir.

O modelo está pronto, embora tenha um erro crítico que será eliminado durante a simulação. O próximo passo é transformar esse modelo conceitual em um modelo para simulação por meio da adição das equações (fórmulas).


UPIS | EAD

Página 15
Módulo 03 - Modelo da Equipe de Trabalho e Estoque
5 - Equações para o modelo equipe1.mdl

Todas as equações para o modelo são listadas abaixo, com suas respectivas unidades. O cadastro correto de cada tipo (level, auxiliary e Constant) é detalhado nos modelos da Unidade IV de Modelagem I. Preste bastante atenção no momento de digitá-las no modelo para evitar erros.

Estoque = INTEG (produção - vendas, 300)
Unidades: perfis

taxa líquida de contratação = (equipe de trabalho desejada - Equipe de trabalho) / tempo para ajustar a equipe de trabalho
Unidades = pessoas/mês

Produção = Equipe de trabalho * produtividade
Unidades: perfis/mês

produção desejada = vendas
unidades: perfis/mês

equipe de trabalho desejada = produção desejada / produtividade
unidades: pessoa

tempo para ajustar a equipe de trabalho = 3
unidades: mês

Produtividade= 1
Unidades: perfis/mês/pessoa


UPIS | EAD

Página 16
Módulo 03 - Modelo da Equipe de Trabalho e Estoque

6 - Dica para a Fórmula de vendas

Todas as variáveis descritas anteriormente geram um comportamento linear ao sistema. Contudo a realidade não é linear, é difusa e complexa. Para aproximar o comportamento dos modelos dinâmicos a realidade podemos atribuir perturbações no sistema e verificar o tempo para ele chegar a um novo equilíbrio.

De acordo com o gerente a produção ajusta-se às vendas, contudo as vendas podem manifestar um comportamento imprevisto. O que aconteceria com a dinâmica do estoque se as vendas aumentassem 50% em um determinado tempo?

O Vensim possui uma série de funções pré-programadas que auxiliam na construção das fórmulas e na simulação de determinadas situações. Uma delas é a função STEP que é utilizada na variável vendas.

vendas = 100 + STEP(50,20)

No caso acima, vendas será 100 até o mês 20 e depois será acrescida de 50 no mês 21, ficando com o valor 150 até o final da simulação, que é de 100 meses.

A função é descrita como:

STEP(A,B)

Onde o valor será zero até o tempo B e, a partir daí, assume o valor A.

Essa variação nas vendas causa certo choque no nosso modelo (assim como causaria em uma indústria, na vida real) e permite analisar como esse efeito se propaga no sistema.


UPIS | EAD

Página 17
Módulo 03 - Modelo da Equipe de Trabalho e Estoque

Inicialmente, estima-se 100 perfis vendidos por mês.

Escolha a função STEP:

Digite 50 no parâmetro height (valor para alterar)

Digite 20 para representar o tempo para atribuir o valor da função STEP.

E acrescente a unidade perfis/mês


UPIS | EAD

Página 18
Módulo 03 - Modelo da Equipe de Trabalho e Estoque
7 - Dica para a Fórmula de Equipe de trabalho

Ao clicar sobre Equipe de trabalho para colocar a fórmula:

Equipe de trabalho = INTEG (taxa líquida de contratação, equipe de trabalho desejada)
Unidades: pessoa

Observe que a variável que deverá ser seu valor inicial, equipe de trabalho desejada, não aparece na relação de variáveis.

Para selecionar essa variável, dê um clique sobre o botão Choose Initial Variable, conforme figura abaixo:


UPIS | EAD

Página 19
Módulo 03 - Modelo da Equipe de Trabalho e Estoque

• Em seguida, selecione equipe de trabalho desejada na lista de variáveis e atrbuindo-a como o valor inicial de Equipe de trabalho.

• Clique OK para confirmar o cadastro da equação:


UPIS | EAD

Página 20
Módulo 03 - Modelo da Equipe de Trabalho e Estoque

• Uma seta cinza fará a conexão entre as duas variáveis.

Obs: Se a seta cinza não aparecer, execute o comando
Model>Settings...
Clique na sua guia Info/Sketch e marque a opção "Show initial causes on model diagrams".

• Redimensione, externamente, a seta cinza, evitando o cruzamento com outras setas.



UPIS | EAD

Página 21
Módulo 03 - Modelo da Equipe de Trabalho e Estoque

8 - Examinando a estrutura

A estrutura do modelo pode ser investigada com as ferramentas de análise. Nesse estágio, responde-se às questões somente sobre a estrutura do modelo e não sobre o comportamento dinâmico do mesmo, que será analisado mais a frente, durante a simulação e com o uso das ferramentas de análise de dados.

• Dê um duplo clique sobre a variável “Estoque” que aparece no modelo para selecioná-la como variável ativa para análise estrutural:

Clique no ícone Causes Tree Diagram no topo da barra de ferramentas de análise. Uma janela será aberta mostrando essa estrutura:

• Pode-se observar que a variável ativa, Estoque, à direita e todas as demais que lhe causam mudanças à esquerda (até dois níveis de distância).


UPIS | EAD

Página 22
Módulo 03 - Modelo da Equipe de Trabalho e Estoque

Não feche a janela Causes Tree. Dê um duplo clique sobre a variável “vendas” que aparece nesta janela para selecioná-la como variável ativa.

Clique no ícone Uses Tree Diagram da barra de ferramentas de análise. Será aberta uma janela sobreposta a janela anterior. Mova a janela para a disposição a seguir:

 

Neste último diagrama pode-se observar onde a variável ativa - vendas - é utilizada no modelo (em quais variáveis ela provoca mudanças). Observe que este diagrama apenas apresenta as informações do modelo de outra maneira. É claro que todas as relações causais podem ser examinadas diretamente no esquema do modelo, no entanto, as representações Uses Tree e Causes Tree torna o modelo mais apresentável e fácil de ser compreendido.

• Clique no ícone Close no canto superior esquerdo , ou no ícone no canto superior direito, ou pressione a tecla Del, para o diagrama de árvore, para cada janela disponível.


UPIS | EAD

Página 23
Módulo 03 - Modelo da Equipe de Trabalho e Estoque

• Dê um duplo clique sobre a variável taxa de contratação que aparece no modelo para selecioná-la.

• Clique no ícone da ferramenta de análise Loops.

Abre-se uma janela que mostra a variável envolvida no feedback associado a variável ativa - taxa de contratação.

• Clique sobre o ícone Document das ferramentas de análise.

A janela que se abre mostra as equações e unidades de medida de todas as variáveis do modelo. Esta ferramenta não se baseia, obviamente, na variável ativa.


UPIS | EAD

Página 24
Módulo 03 - Modelo da Equipe de Trabalho e Estoque

9 - Simulando o modelo

É chegado o momento de examinar o comportamento dinâmico do modelo, examinando suas variáveis. Em particular, desejamos observar a variável Estoque ao longo do tempo. Para isso, necessitamos primeiramente:

Conferir a consistência de unidades do modelo (Ctrl + U):


UPIS | EAD

Página 25
Módulo 03 - Modelo da Equipe de Trabalho e Estoque

Confira a consistência do modelo (Ctrl + T):

Um erro foi identificado no modelo. Trata-se de uma advertência do Vensim verificando a variável Estoque não é usada no modelo. Como o objetivo da dinâmica de sistemas é diagramar modelos que retroalimentam comportamentos, o Vensim verifica as variáveis que não provocam causalidades em outras variáveis (is not used in the model). Podemos marcar a variável como Supplementary, eliminando o erro.


UPIS | EAD

Página 26
Módulo 03 - Modelo da Equipe de Trabalho e Estoque

Confira novamente a consistência do modelo:

Agora podemos simular o modelo.

• Dê um duplo clique na caixa de texto Runname (nome da simulação) na barra de ferramentas para selecionar o nome padrão Current (ou clique e arraste sobre o nome dentro da caixa de texto). Em seguida, digite o nome sim1 . Este será o nome dado ao conjunto de dados (dataset) que armazena os dados resultantes do processo de simulação.

• Clique no ícone de simulação na barra de ferramentas. O Vensim irá simular o modelo e armazenar os dados no dataset denominado sim1.


UPIS | EAD

Página 27
Módulo 03 - Modelo da Equipe de Trabalho e Estoque
Análise

Gere um gráfico para produção e Equipe de trabalho, utilizando a ferramenta Causes Strip, conforme figuras abaixo.

É possível perceber rapidamente que há poucas variações em produção e Equipe de trabalho. Há uma oscilação, basicamente, quando ocorre a mudança nas vendas de 100 perfis/mês para 150 perfis/mês.


UPIS | EAD

Página 28
Módulo 03 - Modelo da Equipe de Trabalho e Estoque
Crie um gráfico para a variável Estoque como mostrado a seguir.

Pode observar que o estoque diminui com certa suavidade do valor inicial de 300 para cerca de 150. Uma vez que o objetivo de se manter um estoque é assegurar que haja mercadorias disponíveis para os clientes, alguma coisa deve estar errada, pois o estoque mensal coincide com as vendas (as vendas são de 150 perfis/mês).

Em outras palavras, o modelo apresenta algum problema, pois não consegue manter um estoque de segurança.


UPIS | EAD

Página 29
Módulo 03 - Modelo da Equipe de Trabalho e Estoque

No sentido de aperfeiçoar o modelo, vamos introduzir as variáveis estoque desejado, ajuste do estoque e duas constantes, margem de segurança e tempo para ajustar o estoque.

A idéia é simples: estoque desejado é a quantidade de mercadorias que devem ser mantidas em estoque, baseada na expectativa de vendas. O ajuste do estoque é uma correção para o desvio do Estoque de seu objetivo.

Salve o seu modelo original (equipe1.mdl). Oportunamente, utilize a opção File-> Publish para publicar seu modelo no formato VPM (Vensim Package Model): equipe1.vpm.

Faça as alterações detalhadas a seguir e salve novamente o modelo renomeado como equipe2.mdl.



UPIS | EAD

Página 30
Módulo 03 - Modelo da Equipe de Trabalho e Estoque

Altere e inclua as equações adicionais conforme a lista a seguir.

produção desejada = vendas + ajuste do estoque
Unidades: perfis/mês

ajuste do estoque = (estoque desejado - Estoque) / tempo para ajustar o estoque
Unidades: perfis/mês

tempo para ajustar o estoque = 2
Unidades: mês

estoque desejado = vendas * margem de segurança
Unidades: perfis

margem de segurança = 3
Unidades: mês

O ajuste do estoque é uma fórmula de ajuste que atua da mesma maneira que taxa líquida de contratação. O tempo para ajustar o estoque representa o tempo necessário para ajustar a produção às novas metas da indústria.



UPIS | EAD

Página 31
Módulo 03 - Modelo da Equipe de Trabalho e Estoque

• Digite o nome sim2 na caixa Runname

Confira a consistência de unidades do modelo (Ctrl + U)

Confira a consistência do modelo (Ctrl + T):

A solução realizada no modelo anterior causou um erro na diagramação atual (The supplementary variable is used / “A variável suplementar é usada”).


UPIS | EAD

Página 32
Módulo 03 - Modelo da Equipe de Trabalho e Estoque

Devemos desmarcar a variável como Supplementary, eliminando o erro.

Confira novamente a consistência do modelo:


UPIS | EAD

Página 33
Módulo 03 - Modelo da Equipe de Trabalho e Estoque

• Simule o modelo. Assegure-se de que sim1 e sim2 estejam carregados no painel de controle e gere um gráfico para Equipe de trabalho.

O comportamento é totalmente diferente do modelo anterior. Equipe de trabalho está muito mais instável com várias oscilações.


UPIS | EAD

Página 34
Módulo 03 - Modelo da Equipe de Trabalho e Estoque
Gere um gráfico para Equipe de trabalho e produção desejada, utilizando a ferramenta Causes Strip.

A variável ajuste do estoque não estava presente na primeira versão do modelo, por isso não há nenhuma linha vermelha referente a sim1, aparecendo no gráfico.


UPIS | EAD

Página 35
Módulo 03 - Modelo da Equipe de Trabalho e Estoque
Todo o comportamento oscilatório de produção desejada é decorrente de ajuste no estoque. Um gráfico de Estoque mostra oscilação semelhante, porém, quando as vendas aumentam, o estoque não cai como na primeira simulação.


UPIS | EAD

Página 36
Módulo 03 - Modelo da Equipe de Trabalho e Estoque

10 – Alterando variáveis exógenas (constantes)

• Clique no ícone Set Up Simulation na barra de ferramentas.

Observe que o texto dos nomes de algumas variáveis aparecem em amarelo sobre um fundo azul. Essas variáveis têm valores pré-definidos (constantes) que não se alteram durante a simulação. Pode-se, entretanto, estabelecer outros valores antes da simulação e observar o efeito das mudanças no comportamento do modelo.

• Clique na variável tempo para ajustar a equipe que aparece em amarelo e azul no diagrama.


UPIS | EAD

Página 37
Módulo 03 - Modelo da Equipe de Trabalho e Estoque

Uma caixa de texto será aberta:

Vamos tentar um experimento no qual será diminuída a taxa de contratação de novos trabalhadores (e de dispensa) para ver se isso remove as oscilações analisadas anteriormente. Idealmente, o que se deseja é diminuir o crescimento do estoque (e da força de trabalho).

• Digite o número 12 na caixa de texto em substituição ao número 3 (isso implica em 12 meses).

• Em seguida, pressione a tecla Enter

• Dê um duplo clique na caixa de texto Runname da barra de ferramentas que contém o nome da simulação e digite o nome sim3.

• Clique no ícone de simulação na barra de ferramentas. O modelo irá simular e armazenar os dados no dataset a sim3.

• Dê um clique duplo na variável Estoque e, em seguida, clique no ícone da ferramenta de análise Graph.

No gráfico são apresentados os resultados dos três experimentos: sim1 (modelo simplificado), sim2 com o valor 3 para a variável tempo para ajustar a equipe e sim3 com o valor da mesma variável alterado para 12. Os valores mostram que uma taxa menor de contração faz crescer e torna mais longa a oscilação (antes a empresa contratava a cada 3 meses e agora alteramos para 12 meses).

Para ver as diferenças nos valores estabelecidos para a variável em cada uma das simulações faça o seguinte:

• Clique no ícone Runs Compare da barra de ferramentas de análise.

A ferramenta mostra os diferentes valores armazenados na variável nas duas simulações (sim2 e sim3).


UPIS | EAD

Página 38
Módulo 03 - Modelo da Equipe de Trabalho e Estoque
11 – Simulação Interativa

Para avaliar como as mudanças nas constantes do modelo (variáveis exógenas) afetam as variáveis endógenas, usamos o recurso simulação interativa das constantes (Automatically simulate on change ).

• Confirme se na caixa de texto Runname da barra de ferramentas que contém o nome da simulação sim3.
• Clique no ícone de simulação na barra de ferramentas.
• O programa advertirá que já existe uma simulação com este nome, perguntando se deseja gravar os novos dados da simulação para um arquivo já existente:

• Confirme a gravação do dataset sim3 com o mesmo nome. Esta operação apagará a última simulação realização com o dataset sim3 (tempo para ajustar a equipe de trabalho =12).
• O modelo apresentará botões deslizantes para alterar as constantes do modelo (tipo constant) e para gráficos minimizados para os demais tipos (level e auxiliary).


UPIS | EAD

Página 39
Módulo 03 - Modelo da Equipe de Trabalho e Estoque

• Outra alternativa para alterar as constantes é clicar com o botão esquerdo do mouse sob as setas, que abrirá uma caixa de diálogo, permitindo atribuição de valores e determinação dos limites e incrementos.
• Vamos proceder as seguintes alterações, clicando com o botão esquerdo do mouse em cada alteração:

o Aumentar a produtividade em 50%

o Aumentar o tempo para ajustar a equipe em 100%

o Aumentar o tempo para ajustar o estoque em 50%


UPIS | EAD

Página 40
Módulo 03 - Modelo da Equipe de Trabalho e Estoque

• Toda variável apresenta um gráfico associado. Apontando o ponteiro do mouse é exibido o gráfico do comportamento da variável.


UPIS | EAD

Página 41
Módulo 03 - Modelo da Equipe de Trabalho e Estoque

• Para maiores detalhes de cada gráfico, ative a variável e exiba com o recurso Graph:

As alterações realizadas nas constantes (sim3) proporcionaram um aumento na oscilação comparada a sim2.

Grave a simulação como sim3, acessando o ícone “Save this run to...”.


UPIS | EAD

Página 42
Módulo 03 - Modelo da Equipe de Trabalho e Estoque

12 - Customizando Gráficos

Algumas vezes há necessidade de ver todas as variáveis importantes juntas em um gráfico. Gráficos gerados a partir das ferramentas de análise mostram o comportamento apenas da variável ativa. Utilizando a ferramenta de customização de gráficos (Custom Graphs) é possível mostrar as variáveis desejadas e conjuntos de dados de simulação (dataset) em um único gráfico. Gráficos customizados são criados a partir do controle de gráficos (Graphs) localizado no Painel de Controle (Control Panel).

• Clique no ícone Control Panel na barra de ferramentas e em seguida na guia Datasets.

• Descarregue o dataset sim1 e sim2 dando um duplo clique sobre cada identificador na caixa Loaded do lado direito.

• Este procedimento exibirá apenas o resultado da simulação sim3.

• Clique na guia Graphs.

• Clique no botão New... O Editor de customização de gráficos será aberto com o cursor posicionado na caixa de texto Title.



UPIS | EAD

Página 43
Módulo 03 - Modelo da Equipe de Trabalho e Estoque

• Digite o nome "Estoque e equipe de trabalho" na caixa de texto Title.

• Usando o mouse, vá para as caixas de texto Variable no lado esquerdo do editor de gráficos e clique no primeiro botão (mais alto) chamado Sel.

• Aparece uma caixa de seleção de variáveis.

• Dê um duplo clique em Equipe de trabalho.

• Clique no segundo botão Sel, logo abaixo do primeiro. A caixa de seleção de variáveis se abre novamente. Dê um clique na variável Estoque e em seguida clique OK para fechar a caixa de seleção.



UPIS | EAD

Página 44
Módulo 03 - Modelo da Equipe de Trabalho e Estoque

• Clique em Ok para fechar o editor de gráficos.

• Clique no botão Display para apresentar o gráfico customizado.


UPIS | EAD

Página 45
Módulo 03 - Modelo da Equipe de Trabalho e Estoque

Vamos focar a oscilação que é nossa área de interesse. No Painel de controle, dê um clique na guia Time Axis para colocar o foco, aproximadamente, entre os meses 18 e 36, conforme figura abaixo.

Gere novamente o gráfico.


UPIS | EAD

Página 46
Módulo 03 - Modelo da Equipe de Trabalho e Estoque

Para fecharmos este módulo com “chave de ouro”, que tal compartilhar seu aprendizado no fórum?

• Utilize o recurso Salvar (ícone disquete):

Divulgue no fórum seu arquivo WMF (Windows Metafile).

Divulgue no fórum o arquivo equipe1.vpm e equipe2.vpm.

Continue por conta própria
Se desejar, continue a analisar a estrutura ou o comportamento do modelo, ou ainda, faça outras simulações alterando os valores das constantes.



UPIS | EAD

Página 47
Módulo 03 - Modelo da Equipe de Trabalho e Estoque
13 - Sensibilidade

É interessante fazer experiências com o modelo, alterando diferentes parâmetros. Uma política para melhorar o desempenho da empresa poderia ser a correção das variações no estoque mais rapidamente. Podemos fazer isso, simulando um prazo menor para tempo para ajustar o estoque, reduzindo-o de 2 para 1 mês, por exemplo.

Diferentes simulações nos levarão a um conhecimento mais profundo do modelo e dos problemas apresentados pela organização, contribuindo, assim, para a busca de melhores soluções antes de implementá-las. Isso pode evitar muitos prejuízos e investimentos desnecessários.


UPIS | EAD

Página 48
Módulo 03 - Modelo da Equipe de Trabalho e Estoque
Resumo

Analisou-se o caso de uma empresa que fabrica e vende perfis para janelas. Embora a empresa esteja indo bem, as oscilações na produção prejudicavam o andamento normal da mesma. Ao invés de culpar a demanda do mercado ou a economia por essas oscilações, procurou-se estudar o comportamento dessa organização.

Para isso, foi construído um modelo simples para reproduzir o comportamento da empresa, cujas vendas pareciam mais estáveis que a produção, o chamado modelo referencial.
Em seguida, foi estabelecida a hipótese dinâmica para essa empresa. A idéia é de que o gerente estabelece a produção, baseado nas vendas, porém sempre aumenta (ou diminui) um pouco a quantidade de modo que, algumas vezes, se produz mais (ou menos) do que seria necessário.

Após simulações e refinamento do modelo, um processo natural na modelagem, percebe-se que a oscilação de vendas para a produção é fisicamente inevitável, ou seja, a mudança na produção deve ser superior à mudança nas vendas por algum tempo no sentido de repor o estoque perdido.


UPIS | EAD
Módulo 2

Página 49
Módulo 04 - Modelo da ocupação de empreendimento hoteleiro

1 - O Problema

Neste ponto, serão focalizadas determinadas características e análises por meio do uso de um modelo organizacional, baseado na taxa de ocupação de um hotel e na eficiência da propaganda.

Em função de sua maior complexidade, e pelo fato de incorporar várias características de comportamento já vistas, constitui um modelo instigante, que irá enriquecer o aprendizado e proporcionar novas idéias sobre modelagem e simulação.

A empresa Businesstrip S.A. acabou de inaugurar o hotel Vitória Business em Vitória (ES). O empreendimento está direcionado para a área de negócios, ou seja, empresários, gerentes, executivos, técnicos e outros profissionais que mantêm negócios naquela capital, configurando uma demanda reprimida de grande potencial.

A empresa tem plena confiança de que será um empreendimento de sucesso. Afinal, foram muitos meses de pesquisa não apenas para identificar uma série de atributos valorizados pelos clientes, como também para identificar e adquirir insumos de qualidade e tecnologias que fizessem do Vitória Business um hotel diferenciado no segmento.



UPIS | EAD

Página 50
Módulo 04 - Modelo da ocupação de empreendimento hoteleiro

Tendo realizado tantos investimentos em qualidade, tecnologia e inovação, a Businesstrip espera obter um alto índice de satisfação dos clientes em relação aos serviços oferecidos pelo hotel. Ela sabe que isso é fundamental para o negócio uma vez que clientes satisfeitos trazem, naturalmente, novos clientes em decorrência da propaganda boca-a-boca. Isso não quer dizer que vá desprezar os canais tradicionais de mídia.

Pelo contrário, esse tipo de investimento é fundamental, principalmente no início das operações, quando poucos conhecem o hotel e não se formou ainda uma massa crítica de ex-clientes suficiente para realizar a propaganda boca-a-boca.

Nosso problema é construir um modelo para analisar a influência da propaganda boca-a-boca e dos investimentos de divulgação na mídia tradicional na ocupação das vagas do Vitória Business.

O modelador entrevistou vários empresários do setor e verificou a seguinte dinâmica qualitativa:


UPIS | EAD

Página 51
Módulo 04 - Modelo da ocupação de empreendimento hoteleiro

O modelo referencial a ser adotado é o de que a ocupação do hotel tenha um rápido crescimento no início, principalmente em função da demanda reprimida e que, em seguida, o índice de ocupação se mantenha alto em função da qualidade dos serviços oferecidos. O comportamento da ocupação deve obedecer a uma curva próxima da apresentada no gráfico, graças à ação da propaganda boca-a-boca e na mídia.

A hipótese dinâmica para o modelo do hotel Vitória Business é de que o papel da propaganda boca-a-boca seja muito mais eficiente do que os investimentos em publicidade na mídia. E, ainda, que a propaganda informal, realizada pelos próprios clientes, só ocorrerá caso se atinjam níveis elevados de satisfação dos hóspedes.


UPIS | EAD

Página 52
Módulo 04 - Modelo da ocupação de empreendimento hoteleiro

2 - Construindo o Modelo

  •  Inicie o Vensim e clique no botão New Model ou execute o comando  File>New Model.

  •  Estabeleça os parâmetros, na caixa de diálogo Time Bounds, como:

    • INITIAL TIME = 0

    • FINAL TIME = 90

    • TIME STEP = 1

    • Units for time = Day

  •  Antes clicar OK, inclua as seguintes unidades de equivalência  somente para este modelo:
    • cliente,clientes,hóspede,hóspedes,pessoa,pessoas
    • real,reais,R$
  •  Salve o modelo como vitoria.mdl.


UPIS | EAD

Página 53
Módulo 04 - Modelo da ocupação de empreendimento hoteleiro

Vamos começar a construção do modelo a partir de um conceito básico de ocupação de um hotel: entram clientes que se tornam hóspedes por um ou mais dias e depois vão embora. Ao estoque, vamos chamar Ocupação do hotel e aos fluxos, entrada de clientes e saída de clientes.

Veja o modelo:


UPIS | EAD

Página 54
Módulo 04 - Modelo da ocupação de empreendimento hoteleiro

Agora, precisamos representar como se dá a entrada de hóspedes. Fazemos isso com uma pergunta bastante óbvia: por que a empresa BusinessTrip construiu um hotel em Vitória? É um empreendimento de vulto e certamente ela não deseja ter prejuízo. Normalmente, as organizações, antes de decidirem por um investimento, fazem pesquisas para avaliar o mercado e, nesse caso, a Businesstrip deve ter identificado uma grande demanda por hospedagens de negócios. Nesse caso, vamos incluir, no modelo, uma variável estoque para representar essa demanda, como mostrado na figura:


Uma vez que o fluxo entrada de hóspedes inicia-se com uma nuvem, para associar com o estoque Demanda devemos:

• Excluir o fluxo entrada de hóspedes:

• Incluir o estoque Demanda:

• Diagramar, novamente, o fluxo entrada de hóspedes, iniciando na Demanda e finalizando na ocupação do hotel.:


UPIS | EAD

Página 55
Módulo 04 - Modelo da ocupação de empreendimento hoteleiro

A demanda é, então, o estoque de pessoas que desejam se hospedar no hotel. Obviamente, se a demanda for maior que as vagas disponíveis, nem todos poderão se hospedar no Vitória Business, criando o que chamamos de "demanda reprimida".

Estes são os dois estoques com os quais vamos trabalhar no momento. Para formar a demanda, temos que criar um fluxo de entrada, representando as pessoas que desejam se hospedar no Vitória Business. Proceda conforme o modelo abaixo:


UPIS | EAD

Página 56
Módulo 04 - Modelo da ocupação de empreendimento hoteleiro

Agora, necessitamos representar como se dá a ocupação do hotel. Obviamente, temos uma limitação que é a capacidade do hotel. Esta foi definida em 300 hóspedes, e a entrada de hóspedes depende do número de vagas disponíveis. Desse modo, a entrada de hóspedes vai ser igual ao número de vagas livres que, por sua vez, é calculado como sendo a capacidade do hotel menos a ocupação do hotel. Já a saída de hóspedes depende da duração média da estada. As ligações são apresentadas na figura abaixo:


UPIS | EAD

Página 57
Módulo 04 - Modelo da ocupação de empreendimento hoteleiro

E os novos clientes? Eles vêm do mercado e são influenciados tanto pela publicidade na mídia, quanto pela propaganda boca-a-boca, realizada pelas pessoas que já se hospedaram. É claro que isso só vai ocorrer se essas pessoas ficarem satisfeitas com os serviços oferecidos pelo hotel. Inclua, inicialmente, o mercado, como mostrado na figura abaixo:

 


UPIS | EAD

Página 58
Módulo 04 - Modelo da ocupação de empreendimento hoteleiro

3 - Criando o Comportamento da Publicidade

Pesquisas indicaram que para cada R$ 10,00 gastos com publicidade, o hotel consegue um novo cliente. Essa relação linear é definida pela variável fator publicidade a partir do valor do investimento em publicidade que pode ser realizado. Ele será adicionado à variável novos clientes. Observe a figura abaixo:


UPIS | EAD

Página 59
Módulo 04 - Modelo da ocupação de empreendimento hoteleiro

Para criar comportamento da publicidade boca-a-boca, vamos supor um fato muito comum em várias organizações: a pesquisa de satisfação. Por meio da aplicação de várias técnicas estatísticas é possível capturar e converter a satisfação (ou a insatisfação) dos clientes em um índice geral. No caso do nosso modelo, vamos chamá-lo de Índice Geral de Satisfação (IGS) que poderá variar de 0 a 10 (como se fosse uma nota geral dada pelos clientes aos serviços prestados pelo hotel). Esse índice define o fator de propaganda, um fator que multiplicado pelo tamanho do mercado dá a quantidade de clientes que o hotel ganha graças a esse tipo de propaganda.

No nosso modelo fizemos a seguinte escala:

IGS >= 7    ==>      fator de publicidade = 0.003 (equivale a 0.3%)
IGS >= 5    ==>      fator de publicidade = 0.001 (equivale a 0.1%)
IGS < 5      ==>      fator de publicidade = 0

Para implementar essa escala, utilizaremos a função IF THEN ELSE do Vensim.


UPIS | EAD

Página 60
Módulo 04 - Modelo da ocupação de empreendimento hoteleiro

O formato geral da equação é:

IF THEN ELSE( {cond} , {ontrue} , {onfalse} ), onde:

{cond} é a condição que queremos testar;
{ontrue} é o valor que será assumido pela variável se a condição for verdadeira;
{onfalse} é o valor que será assumido pela variável se a condição for falsa.

No nosso caso, precisaremos utilizar duas funções IF THEN ELSE, como mostrado:

IF THEN ELSE(índice geral de satisfação>=7, 0.003*índice geral de satisfação , IF THEN ELSE(índice geral de satisfação>=5, 0.001*índice geral de satisfação ,0 ) ).


UPIS | EAD

Página 61
Módulo 04 - Modelo da ocupação de empreendimento hoteleiro

Para completar o modelo, faça as alterações conforme a figura:

Podemos conferir a estrutura linear (causes tree e uses tree) ou a estrutura dinâmica de qualquer variável. Seguem esses recursos aplicados ao fluxo “entrada de hóspedes”:

4 – Inserindo as fórmulas

Essa primeira versão do programa está pronta. Insira as fórmulas conforme mostrado na próxima página para que possamos simular o modelo.



UPIS | EAD

Página 62
Módulo 04 - Modelo da ocupação de empreendimento hoteleiro

investimento em publicidade na mídia = 100
Unidades: reais

fator publicidade = investimento em publicidade na mídia / 10
Unidades: pessoas

mercado = 5000
Unidades: pessoas

índice geral de satisfação = 9
Unidades: Dmnl (sem dimensões)

fator de propaganda: IF THEN ELSE(índice geral de satisfação>=7, 0.003*índice geral de satisfação , IF THEN ELSE(índice geral de satisfação>=5, 0.001*índice geral de satisfação ,0 ) )
Unidades: Dmnl (sem dimensões)

novos clientes = (mercado*fator de propaganda)+fator publicidade
Unidades = clientes/dia

demanda = INTEG(novos clientes-entrada de hóspedes,500)
Unidades = clientes

entrada de hóspedes = IF THEN ELSE(Demanda>vagas livres , vagas livres
,Demanda)
Unidades: hóspedes/dia

capacidade do hotel = 300
Unidades: hóspedes

vagas livres = capacidade do hotel-Ocupação do hotel
Unidades: hóspedes

Ocupação do hotel = INTEG(entrada de hóspedes-saída de hóspedes,0)
Unidades: hóspedes

duração média da estadia = 3
Unidades: dias

saída de hóspedes = (Ocupação do hotel/duração média da estadia)
unidades: hóspedes/dia.

5 – Conferindo a consistência

Confira a consistência do modelo (Ctrl + T):


UPIS | EAD

Página 63
Módulo 04 - Modelo da ocupação de empreendimento hoteleiro

Confira a consistência de unidades do modelo (Ctrl + U)

É necessário revisar o modelo que apresenta 3 equações com inconsistência de unidades. Se você encontrou mais que 3 erros, revisar as unidades equivalentes em Model/Settings ou a digitação das unidades de cada equação.

Vamos revisar um conceito apresentado anteriormente?

Portanto, em um modelo quantitativo, os fluxos e estoques regem as unidades a “jusante” e a “montante” do modelo. Vamos avaliar cada erro separadamente (com a respectiva tradução didática) e verificar uma solução possível.

É indispensável que o aluno acompanhe esse raciocínio matemático com um papel e uma caneta, transcrevendo cada passo e acompanhando o que está sendo avaliado no diagrama do modelo hotel.mdl no Vensim.

Qualquer dúvida deve ser encaminhada no fórum ou e-mail do professor. Evite acumular dúvidas, que podem prejudicar o real aprendizado em todas as fases posteriores do conteúdo.


Um aspecto importante na simulação dinâmica é atribuir corretamente unidades às estruturas do diagrama de fluxos e estoques.

Os fluxos sempre possuem no denominador uma unidade temporal (segundos, dias, ano, etc.)

A simulação dinâmica consiste em avaliar, quantitativamente, o modelo em cada intervalo de tempo.

Portanto os estoques (acumulações do estado de um sistema em um determinado tempo) NÃO APRESENTAM UNIDADES DE TEMPO


Jusante: “o sentido da correnteza num curso de água (da nascente para foz)” Dicionário Houaiss. Seguem as variáveis a jusante do fluxo “novos clientes”:


Montante: “subida de maré”; “antônimo de jusante” Dicionário Houaiss. Seguem as variáveis a montante do fluxo “novos clientes”:


UPIS | EAD

Página 64
Módulo 04 - Modelo da ocupação de empreendimento hoteleiro

Análise da unidade incoerente à equação novos clientes:

Error in units for the following equation:
novos clientes =
     ( mercado
          * fator de propaganda )
          + fator publicidade

novos clientes --> clientes/dia
mercado --> pessoas
fator de propaganda --> Dmnl
fator publicidade --> pessoas

Analysis of units error:
Right hand and left hand units do not match
novos clientes
Has Units: clientes/Day
      ( mercado
           * fator de propaganda )
           + fator publicidado

Has Units: clientes

Tradução:

Erro nas unidades para a seguinte equação:
novos clientes =
     ( mercado
          * fator de propaganda )
          + fator publicidade

novos clientes --> clientes/dia
mercado --> pessoas
fator de propaganda --> Dmnl
fator publicidade --> pessoas

Análise dos erros nas unidades:
Não coincidem as unidades do lado direito (destacado com fundo azul) e do lado esquerdo (destacado com fundo laranja) da equação:


UPIS | EAD

Página 65
Módulo 04 - Modelo da ocupação de empreendimento hoteleiro

O erro refere-se que as variáveis que determinam o valor do fluxo novos clientes não apresenta unidades clientes/dia (lembre que clientes e pessoas são sinônimos).

O fluxo é representando corretamente com as unidades clientes/dia. Portanto a incosistência das unidades é gerada pelas variáveis à jusante:

Devemos verificar a fórmula:
( mercado * fator de propaganda ) + fator publicidade

Equação
Unidade resultante
(mercado * fator de propaganda)
pessoas*dmnl = pessoas
fator publicidade
pessoas
(mercado * fator de propaganda) + fator publicidade
pessoas + pessoas = pessoas = cliente

E alterar as unidades coerentes com o fluxo (clientes/dia ou pessoas/dia).

Equação relacionada
Unidade corrigida
(mercado * fator de propaganda) + fator publicidade
clientes/dia = pessoas/dia


UPIS | EAD

Página 66
Módulo 04 - Modelo da ocupação de empreendimento hoteleiro
Portanto, toda a equação deve resultar na unidade pessoas/dia. A equação inclui uma soma de 2 termos, então cada termo deve apresentar a unidade pessoas/dia.

Variável auxiliar fator publicidade: será alterada para pessoas/dia.
Justificativa: a publicidade, realizada diariamente, favorecerá o aumento dos novos clientes/dia.

Equação relacionada
Unidade corrigida
fator publicidade
pessoas/dia

Equação (mercado * fator de propaganda):
A constante mercado possui unidade coerente (pessoas). Se o resultado da equação deve ser pessoas/dia, qual deve ser a unidade da variável auxiliar fator de propaganda?

Equação relacionada
Unidade corrigida
(mercado * fator de propaganda)
pessoas/dia


UPIS | EAD

Página 67
Módulo 04 - Modelo da ocupação de empreendimento hoteleiro

Devemos substituir as unidades coerentes e verificar qual unidade da variável auxiliar fator de propaganda garante a consistência de unidades da equação:

mercado * fator de propaganda = pessoas * fator de propaganda =
pessoas
dia
pessoas * fator de propaganda =
pessoas
dia

Isolando fator de propaganda:

fator de propaganda =
    pessoas    
dia * pessoas
 

Cancelando unidades em comum:

fator de propaganda =
    pessoas    
dia * pessoas
 

fator de propaganda garante a consistência associada a unidade:

fator de propaganda =
  1  
dia
=
fraction
dia

A unidade fraction/dia é coerente?


UPIS | EAD

Página 68
Módulo 04 - Modelo da ocupação de empreendimento hoteleiro

Se a unidade não for coerente devemos revisar nosso modelo mental e a realidade investigada, pois a variável auxiliar pode agregar o comportamento de várias outras variáveis implícitas...

Todavia, a unidade obtida algebricamente é coerente. A variável auxiliar fator de propaganda extrai do contingente pessoas do mercado uma alíquota de clientes para o empreendimento hoteleiro (propaganda boca-a-boca).

Concordamos em realizar as seguintes alterações:

Variável auxiliar fator publicidade: pessoas/dia

Variável auxiliar fator de propaganda: fraction/dia

Como o índice geral de satisfação causa modificação no fator de propaganda, o índice geral de satisfação também deve ser alterado para fraction/dia.

Variável auxiliar índice geral de satisfação: fraction/dia

Altere as unidades de “fator publicidade”, “fator de propaganda” e índice geral de satisfação”.
Confira a consistência de unidades do modelo (Ctrl + U).


UPIS | EAD

Página 69
Módulo 04 - Modelo da ocupação de empreendimento hoteleiro
Análise da unidade incoerente à equação fator publicidade:

Existe um erro na consistência de unidades associado a “fator publicidade”.

Lembre que já concordamos que o fator publicidade deve apresentar a unidade pessoas/dia.

Se à montante da variável “fator publicidade” as unidades estão corretas:

Devemos revisar as variáveis à jusante do “fator publicidade”:

Error in units for the following equation:
fator publicidade =
       investimento em publicidade na mídia
            / 10
fator publicidade --> pessoas/dia
investimento em publicidade na mídia --> reais

Analysis of units error:
Right hand and left hand units do not match
fator publicidade
Has Units: clientes/Day
investimento em publicidade na mídia
     / 10
Has Units: reais

Tradução:

Erro na unidade para a seguinte equação:
fator publicidade =
        investimento em publicidade na mídia
             / 10
fator publicidade --> pessoas/dia
investimento em publicidade na mídia --> reais

Análise dos erros nas unidades:
Não coincidem as unidades do lado direito e do lado esquerdo da equação:
fator publicidade
Has Units: clientes/Day
investimento em publicidade na mídia
     / 10
Has Units: reais


UPIS | EAD

Página 70
Módulo 04 - Modelo da ocupação de empreendimento hoteleiro
Não podemos alterar, integralmente, todas as unidades das variáveis e constantes anteriores para pessoas/dia. A unidade reais tem coerência para o investimento em publicidade na mídia, contudo falta adicionar-lhe temporalidade. O empreendimento investirá, diariamente R$ 100,00. Portanto a unidade deve ser alterada para reais/dia.

Contudo, ainda permanece incoerente:

fator publicidade = investimento em publicidade na mídia/10
(pessoas/dia) = reais por dia

Esse é o caso que existe uma variável implícita na equação que, neste momento, deve ser incorporada no modelo.

Um indicativo é o divisor 10. Para a realidade investigada, sugerimos que R$ 100,00 investidos por dia retornam 10 pessoas (ou a décima parte) adicionados para o fluxo novos clientes.


UPIS | EAD

Página 71
Módulo 04 - Modelo da ocupação de empreendimento hoteleiro

Portanto, devemos criar uma nova variável associada ao fator de publicidade: retorno da publicidade:

Alterando a equação:
fator de publicidade = investimento em publicidade na mídia/retorno da publicidade

Se concordamos com as unidades:
fator de publicidade = pessoas/dia
investimento em publicidade na mídia = reais/dia

Qual deve ser a unidade da constante retorno da publicidade?



UPIS | EAD

Página 72
Módulo 04 - Modelo da ocupação de empreendimento hoteleiro
fator de publicidade =
investimento em publicidade na mídia
retorno da publicidade

 

pessoas
dia
=
reais
          ___   dia ___             
retorno da publicidade

Isolando retorno da publicidade:

retorno da publicidade =
reais
             dia              
pessoas
dia

Cancelado unidades em comum:

retorno da publicidade =
 reais 
             dia              
pessoas
dia

retorno da publicidade garante a consistência associada a unidade:

retorno da publicidade =
reais
pessoas
(plural)
=
reais
pessoas
(singular)

A unidade reais/pessoa é coerente?


UPIS | EAD

Página 73
Módulo 04 - Modelo da ocupação de empreendimento hoteleiro

A constante retorno da publicidade sendo divisora do investimento em publicidade na mídia apresenta unidade coerente, indicando que uma pessoa é convertida em cliente a cada R$ 10,00.

Concordamos em realizar a seguinte alteração:

Concordamos em realizar a seguinte alteração: retorno da publicidade = 10 unidade = reais/pessoa

Altere a unidade da constantes “retorno da publicidade” e confira a consistência de unidades do modelo.



UPIS | EAD

Página 74
Módulo 04 - Modelo da ocupação de empreendimento hoteleiro
Análise da unidade incoerente à equação entrada de hóspedes:

Segue a última inconsistência de unidades do modelo:

Error in units for the following equation:
entrada de hóspedes =
        IF THEN ELSE ( Demanda
                 > vagas livres ,
             vagas livres ,
             Demanda )
entrada de hóspedes --> hóspedes/dia
Demanda --> clientes
vagas livres --> hóspedes
vagas livres --> hóspedes
Demanda --> clientes

Analysis of units error:
Right hand and left hand units do not match
entrada de hóspedes
Has Units: clientes/Day
IF THEN ELSE ( Demanda
         > vagas livres ,
     vagas livres ,
     Demanda )
Has Units: clientes

Tradução:

Erro nas unidades para a seguinte equação:
entrada de hóspedes =
        IF THEN ELSE ( Demanda
                 > vagas livres ,
            vagas livres ,
            Demanda )
entrada de hóspedes --> hóspedes/dia
Demanda --> clientes
vagas livres --> hóspedes
vagas livres --> hóspedes
Demanda --> clientes

Análise dos erros nas unidades:
Não coincidem as unidades do lado direito e do lado esquerdo da equação:
entrada de hóspedes
Tem unidades: clientes/Day
IF THEN ELSE ( Demanda
         > vagas livres ,
    vagas livres ,
    Demanda )
Tem unidades: clientes


UPIS | EAD

Página 75
Módulo 04 - Modelo da ocupação de empreendimento hoteleiro
Este problema é típico quando relacionamos, em uma mesma equação, um fluxo e um estoque. Teoricamente, necessitamos de uma variável auxiliar para acrescentar temporabilidade no estoque e comparar com as variáveis dependentes do fluxo. Como obtivemos êxito no modelo clientes2.mdl? Verifique que o Estoque recebe a temporalidade com a constante tempo para ajustar o estoque, garantindo a consistência de unidades do modelo.



UPIS | EAD

Página 76
Módulo 04 - Modelo da ocupação de empreendimento hoteleiro

Sempre que possível, incorporem uma variável temporal para ajustar os fluxos/estoque. Os fluxos deveriam modificar os estoques gradualmente. Este comportamento é desejado para representar a realidade dinâmica presente na maioria das organizações:

Mudanças instantâneas ou abruptas são raras.


UPIS | EAD

Página 77
Módulo 04 - Modelo da ocupação de empreendimento hoteleiro
Para o modelo simplificado vitoria.mdl, vamos optarpor não incorporar a temporalidade na associação do estoque com o fluxo. Se os fluxos exigem temporalidade e estoques não permitem temporalidade, como podemos resolver esse impasse?.

Vamos criar uma constante (conversor para garantir a consistência de unidades) denominada temporalidade dos estoques, acrescentando a temporalidade nas equações que dependem dos estoques:


UPIS | EAD

Página 78
Módulo 04 - Modelo da ocupação de empreendimento hoteleiro

Editando a constante temporalidade do estoque conforme detalhamento a seguir:

E alterando o fluxo entrada de hóspedes:


UPIS | EAD

Página 79
Módulo 04 - Modelo da ocupação de empreendimento hoteleiro

Podemos garantir a consistência de unidades do modelo.


UPIS | EAD

Página 80
Módulo 04 - Modelo da ocupação de empreendimento hoteleiro

6 – Simulando o Modelo

Digite o nome hotel1 na caixa de edição runname e simule o modelo.

Análise

Gere um gráfico para Ocupação do hotel, utilizando a ferramenta Graph, conforme figura abaixo.

Podemos observar que o comportamento da Ocupação do hotel assemelha-se ao nosso modelo referencial, ou seja, a entrada de hóspedes é exponencial e se estabiliza em torno de 225 clientes dadas as condições iniciais do modelo.


UPIS | EAD

Página 81
Módulo 04 - Modelo da ocupação de empreendimento hoteleiro

Vamos fazer agora algumas mudanças. Vamos diminuir a satisfação do cliente para um valor intermediário, seis, por exemplo. Isso corresponderia a uma satisfação mediana dos hóspedes. Dê outro nome para a simulação para que possamos comparar as duas execuções (por exemplo, hotel 2). O resultado pode ser observado no gráfico:

Podemos observar que o comportamento da Ocupação do hotel é parecido, no início, com o da primeira simulação. Porém, o efeito da propaganda boca-a-boca já não é mais o mesmo, fixando uma ocupação bem menor para o hotel, em torno de 120 hóspedes/dia.


UPIS | EAD

Página 82
Módulo 04 - Modelo da ocupação de empreendimento hoteleiro

Para realizar a terceira simulação, vamos retornar o índice de satisfação para nove, como no início, e reduzir a propaganda na mídia para zero, ou seja, não será feito nenhum investimento em publicidade. Execute a simulação, dando-lhe um terceiro nome, e observe o resultado no gráfico abaixo:

A conclusão é que a publicidade não alterou em nada a ocupação do hotel, uma vez que a demanda já era por si suficientemente alta. Mas será que a publicidade não teria nenhum efeito na ocupação do hotel? Vamos realizar mais um experimento.


UPIS | EAD

Página 83
Módulo 04 - Modelo da ocupação de empreendimento hoteleiro

Vamos retirar totalmente o efeito da propaganda boca-a-boca, reduzindo o índice geral de satisfação para zero. Em seguida, mantemos um investimento de 100 reais/dia em publicidade.

Parece que o investimento em publicidade ajuda a manter pelo menos 10% de ocupação do Vitória, em torno de 30 clientes. Mas será que é isso mesmo? Que tal reduzir esse investimento para zero e observar o que acontece? Nessa última simulação, o hotel não terá nenhum tipo de divulgação, nem boca-a-boca nem em publicidade.


O vensim adverte que já existe um dataset com o nome hotel3 (Dataset hotel3 already exists) e pergunta se deseja sobrescrever os dados (Do you want to overwrite it?). Confirme (Sim) para manter o mesmo nome (hotel3) com a nova simulação.


UPIS | EAD

Página 84
Módulo 04 - Modelo da ocupação de empreendimento hoteleiro

O gráfico nos leva a crer que, em menos de 20 dias, o hotel não teria mais condições de sobreviver, uma vez que a tendência é a ocupação cair para limites próximos de zero.


UPIS | EAD

Página 85
Módulo 04 - Modelo da ocupação de empreendimento hoteleiro

Podemos concluir então, baseados no comportamento de nosso modelo, alguns fatos importantes:

  • se a qualidade dos serviços oferecidos for insatisfatória e não houver publicidade, o empreendimento se tornará inviável e tenderá a ir a falência;
  • o efeito da propaganda boca-a-boca na ocupação do hotel é muito mais significativo do que o investimento em publicidade;
  • apesar de não termos analisado custos, investir em publicidade também diminui a margem de lucro por cliente, o que pode representar riscos para o empreendimento;
  • investir na qualidade dos serviços ainda é a melhor opção para esse e outros empreendimentos.

Restrinja o período de análise até 30 dias e realize simulações adicionais, utilizando o recurso “simulate on change”

Publique o modelo como vitória.vpm e divulgue no fórum.


UPIS | EAD

Página 86
Módulo 04 - Modelo da ocupação de empreendimento hoteleiro

Resumo

Encerra o curso com a construção de um modelo que representa processos clássicos e muito discutidos dentro da área de administração: o efeito da propaganda boca-a-boca, da publicidade, da qualidade e satisfação do cliente.
Todos esses tópicos foram reunidos em único modelo que permite múltiplas simulações em sua riqueza de variáveis e constantes que podem ser alteradas, voltando o modelo a ser simulado e analisado sob diferentes situações.

As principais conclusões, após algumas simulações, são:

  • se a qualidade dos serviços oferecidos for insatisfatória e não houver publicidade, o empreendimento se tornará inviável e tenderá a ir a falência;
  • o efeito da propaganda boca-a-boca na ocupação do hotel é muito mais significativo do que o investimento em publicidade;
  • apesar de não termos analisado custos, investir em publicidade também diminui a margem de lucro por cliente, o que pode representar riscos para o empreendimento;
  • investir na qualidade dos serviços ainda é a melhor opção para esse e outros empreendimentos.