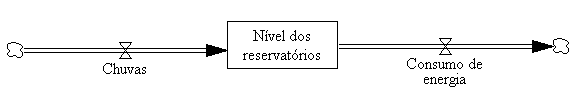Módulo 1

Página 1
Módulo 01 - Estrutura e Comportamento de Sistemas Dinâmicos
1 - Modos Fundamentais de Comportamento Dinâmico

O comportamento de um sistema deriva de sua estrutura, que consiste dos feedbacks, dos estoques e fluxos e das interações entre a estrutura física e a institucional, da qual faz parte o processo de tomada de decisão por agentes que retroalimentam o sistema. Este módulo oferece uma visão geral do relacionamento entre a estrutura e o comportamento dos sistemas dinâmicos. Os modos fundamentais de comportamento dos sistemas são identificados ao longo das estruturas de feedbacks que os geram. Esses modelos incluem o crescimento, criado pelos feedbacks positivos; a busca de um objetivo, criado por um feedback negativo e as oscilações, criadas por feedbacks negativos com algum tipo de atraso na resposta do sistema. Também serão abordados modelos mais complexos, como o crescimento em forma de S, o crescimento com oscilação e o crescimento e colapso, que se originam de interações não lineares das estruturas básicas dos sistemas.


UPIS | EAD

Página 2
Módulo 01 - Estrutura e Comportamento de Sistemas Dinâmicos
Dinâmica significa mudança e a quantidade e variedade a que estamos assistindo nos dias atuais é assustadora. Podemos imaginar que para lidar com tantas mudanças deve existir uma quantidade correspondente de feedbacks negativos. Na realidade, muitas mudanças são decorrentes de pequeno número de padrões de comportamento, como o crescimento exponencial ou a oscilação. Nos gráficos abaixo são apresentados alguns dos modos de comportamento mais comuns.

Desses mais comuns apresentados, os modos fundamentais de comportamento dinâmico são o crescimento exponencial, a busca de um objetivo e a oscilação.


UPIS | EAD

Página 3
Módulo 01 - Estrutura e Comportamento de Sistemas Dinâmicos
2 - O Crescimento Exponencial

O crescimento exponencial é decorrente de um feedback positivo. Alguns exemplos já vistos foram populações, juros, conhecimento, poder, etc. O chamado crescimento exponencial "puro" tem a propriedade de dobrar o tamanho do sistema em um período de tempo fixo. O tempo gasto para ir do tamanho 1 ao 2 é exatamente o mesmo gasto para ir do tamanho 1 milhão para 2 milhões. Essa propriedade é uma conseqüência direta do feedback positivo.

E o crescimento linear? Esse tipo de crescimento é, atualmente, cada vez mais raro. Ele requer que não exista um feedback entre o sistema e sua taxa de crescimento, que se mantém constante independentemente das mudanças e tamanho do sistema. Além disso, muitas coisas que aparentam ter um crescimento linear estão sendo analisadas em curtos períodos de tempo, de modo que é difícil observar sua aceleração.

Os gráficos a seguir mostram alguns exemplos de crescimento exponencial. As curvas que representam o crescimento desses sistemas nem sempre são perfeitas, devido às variações nas taxas de crescimento, nos feedbacks e outras perturbações do ambiente. O importante é notar o comportamento dominante no modelo.


UPIS | EAD

Página 4
Módulo 01 - Estrutura e Comportamento de Sistemas Dinâmicos



UPIS | EAD

Página 5
Módulo 01 - Estrutura e Comportamento de Sistemas Dinâmicos
3 - A busca de um objetivo

Os feedbacks positivos promovem o crescimento e a mudança. Já os negativos negam a mudança e tendem para o equilíbrio e podem agir no sentido de que um determinado sistema se oriente a um determinado objetivo. Para isso, o estado atual do sistema é comparado com o objetivo. Se existir alguma discrepância, ações corretivas vão ser tomadas para conduzir o sistema aos seus objetivos. Quando temos fome nos alimentamos, se estamos cansados, dormimos para restaurar as energias. Se os estoques de uma empresa caem abaixo do mínimo, novos pedidos de suprimentos serão feitos.

Cada feedback negativo inclui um processo para comparar a condição atual com a condição desejada e as ações corretivas a serem tomadas. Em alguns casos o objetivo de um sistema e as ações a serem tomadas são explícitas e controladas por um decisor (o gerente de compras, no exemplo dos estoques). Em outros casos, tanto os objetivos e as ações encontram-se implícitos. A quantidade de sono que necessitamos, por exemplo, é um fator psicológico que foge ao controle do consciente. O equilíbrio da temperatura da terra depende do fluxo de energia solar, da vegetação e dos gases presentes na atmosfera, entre outros fatores físicos. Uma xícara de café quente esfria por meio de um feedback negativo até o seu objetivo, que é a temperatura do ambiente (apesar de preferirmos café quente).


UPIS | EAD

Página 6
Módulo 01 - Estrutura e Comportamento de Sistemas Dinâmicos
Em alguns casos, a taxa pela qual um sistema se aproxima de seu objetivo diminui à medida que a discrepância é menor. É raro encontrar uma taxa de aproximação constante e que, assim que o objetivo é atingido, se reduz a zero. A taxa de aproximação é gradual porque a diferença entre o estado atual do sistema e seus objetivos é grande e se reduz na mesma proporção em que diminui a diferença.

Os gráficos a seguir mostram sistemas que têm comportamento orientado a um objetivo.


UPIS | EAD

Página 7
Módulo 01 - Estrutura e Comportamento de Sistemas Dinâmicos
4 - Oscilação

A oscilação é o terceiro modo fundamental de comportamento observado nos sistemas dinâmicos. Assim como a busca de um objetivo, as oscilações são causadas por um feedback negativo. O estado do sistema é comparado com seu objetivo e medidas corretivas são tomadas no sentido de eliminar as discrepâncias. Contudo, o objetivo é sempre ultrapassado, gerando o movimento oscilatório. Esse problema tem origem em "atrasos" no sistema 'que causam ações corretivas contínuas, que não param quando o sistema atingiu seu objetivo, forçando o mesmo a um ajuste e gerando uma nova correção no sentido inverso.

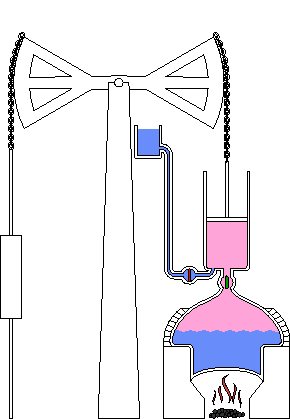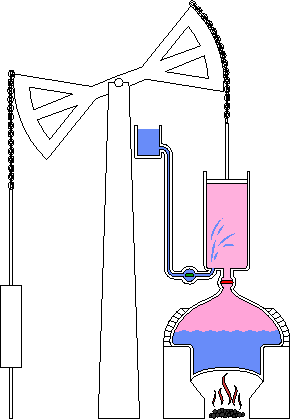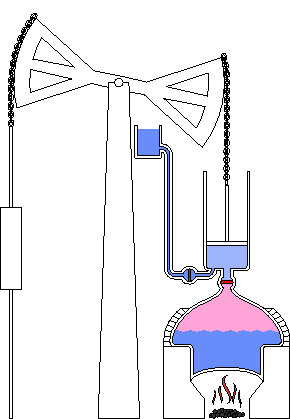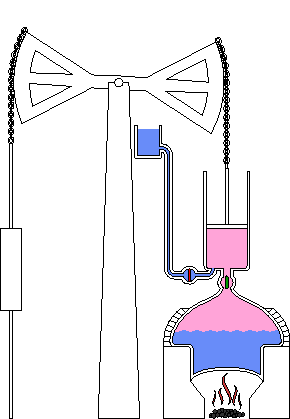
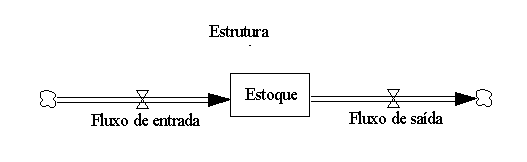
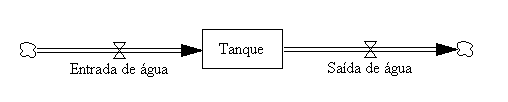
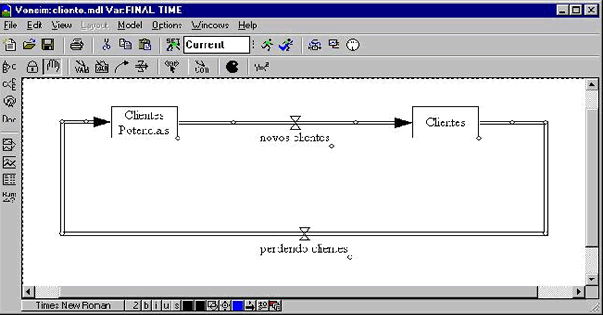
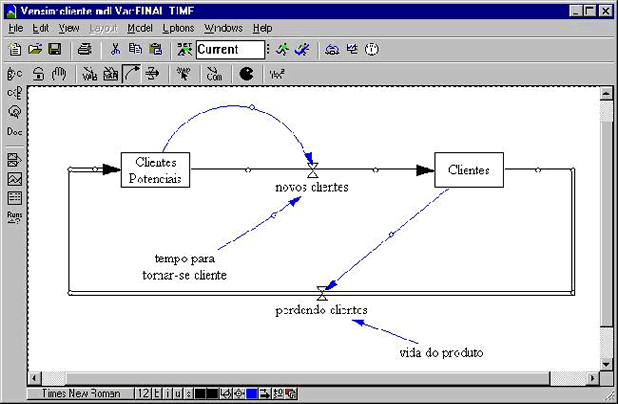
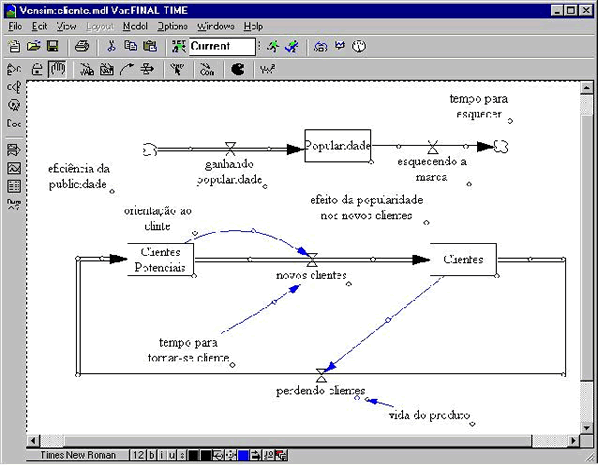
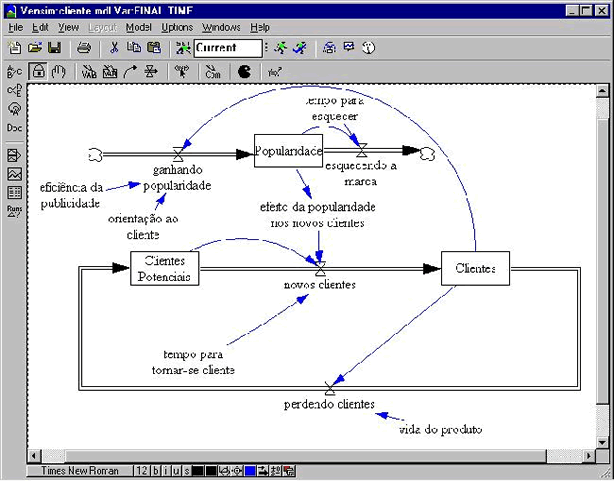
As oscilações estão entre os modos mais comuns de comportamento de sistemas. Como mostrado na figura abaixo, podem ocorrer atrasos nas informações do ciclo.

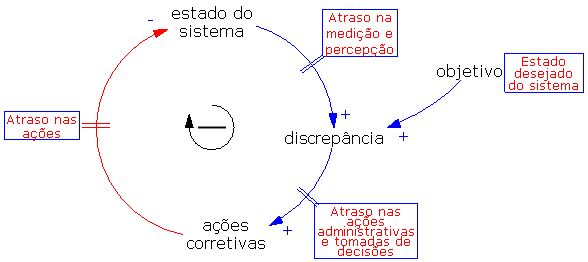
Pode ocorrer atraso na medição e percepção, nas ações administrativas e tomada de decisões e entre o início das ações corretivas e seu efeito no estado do sistema. Em uma empresa, por exemplo, leva tempo para se medir e fazer os relatórios dos estoques, leva tempo para os gerentes decidirem qual a quantidade a ser produzida, leva tempo para as matérias-primas chegarem na empresa, leva tempo para os produtos serem confeccionados, etc. Se esses atrasos forem longos haverá oscilação nos estoques da empresa.


UPIS | EAD

Página 8
Módulo 01 - Estrutura e Comportamento de Sistemas Dinâmicos
As oscilações nos sistemas de negócios (e em muitos outros sistemas da vida real) não são perfeitamente regulares e nem poderíamos esperar que fossem. Muitas pessoas imaginam que os sistemas são previsíveis como a órbita dos planetas ou o balanço do pêndulo de um relógio. Os planetas são controlados por rígidas forças universais e os pêndulos são cuidadosamente desenhados para gerar o movimento. Sistemas biológicos, sociais e econômicos, pelo contrário, são constantemente bombardeados por perturbações que fazem com que o movimento oscilatório ocorra, porém de uma maneira irregular. Isso é o que pode ser visto nos gráficos a seguir.



UPIS | EAD

Página 9
Módulo 01 - Estrutura e Comportamento de Sistemas Dinâmicos
5 - Interações dos modos fundamentais

Os três modos básicos de comportamento - crescimento exponencial, busca de um objetivo e oscilação - são causados por três estruturas básicas de feedbacks: feedback positivo, feedback negativo e feedback negativo com atrasos. Outros padrões mais complexos de comportamento ocorrem devido às interações não lineares dessas estruturas com outras.


UPIS | EAD

Página 10
Módulo 01 - Estrutura e Comportamento de Sistemas Dinâmicos

6 - Crescimento em forma de S

Nada pode crescer (ou diminuir) para sempre: em um momento ou outro esse crescimento será constrangido. Um modo comum de comportamento em sistemas dinâmicos é o crescimento em formato de S. O crescimento, no princípio, é exponencial mas, gradualmente, a velocidade de crescimento vai diminuindo até que o sistema encontra seu equilíbrio. O formato da curva lembra um S, daí o seu nome. Para que este comportamento seja melhor compreendido vamos utilizar um exemplo ecológico.

A capacidade de um determinado ecossistema suportar uma população de organismos é determinado pela disponibilidade de recursos no ambiente e pelas necessidades dessa população. À medida que a população se aproxima do limite do ecossistema os recursos disponíveis per capita vão diminuindo até que o equilíbrio populacional é encontrado.


UPIS | EAD

Página 11
Módulo 01 - Estrutura e Comportamento de Sistemas Dinâmicos
Similarmente, os negócios e as organizações crescem no contexto de um mercado que impõe limites aos seus crescimentos. Esses limites, como nas populações, podem variar em função das interações das empresas com seus clientes, fornecedores, funcionários, tecnologias, governo e outras entidades presentes no mercado. Os gráficos a seguir mostram alguns exemplos de crescimento em formato de S. Seja o crescimento de uma planta, a difusão de um novo produto ou serviço (como a TV a cabo) ou a adoção de uma nova idéia ou tecnologia, o crescimento sempre encontra os seus limites.


UPIS | EAD

Página 12
Módulo 01 - Estrutura e Comportamento de Sistemas Dinâmicos

7 - Crescimento em forma de S com oscilação

O crescimento em forma de S necessita que o feedback negativo aja rapidamente diminuindo o crescimento à medida que o sistema se aproxima de seu limite. Algumas vezes, entretanto, ocorrem significativos atrasos no feedback negativo levando à possibilidade de que o sistema ultrapasse um pouco o seu limite, retorne, em função das ações desencadeadas e fique oscilando. Dois exemplos são apresentados nos gráficos a seguir:


UPIS | EAD

Página 13
Módulo 01 - Estrutura e Comportamento de Sistemas Dinâmicos
8 - Crescimento e Colapso

Um fator crítico do crescimento em forma de S é que o limite dos sistemas é fixo. No entanto, algumas vezes esses limites podem ser rompidos, como no caso do crescimento de uma população. Quando isso ocorre é possível que os recursos do ambiente se esgotem e os indivíduos comecem a morrer de fome e doença provocando o declínio. Se não houver uma regeneração da capacidade do sistema (se os recursos não são renováveis, por exemplo) o sistema tenderá para a extinção.


UPIS | EAD

Página 14
Módulo 01 - Estrutura e Comportamento de Sistemas Dinâmicos
No mundo dos negócios podemos ver esse comportamento no ciclo de vida de um produto. É o caso das vendas da Atari, por exemplo, mostrado em um dos gráficos a seguir.



UPIS | EAD

Página 15
Módulo 01 - Estrutura e Comportamento de Sistemas Dinâmicos

Outros modos de comportamento

Os modos de comportamento mostrados nos itens anteriores são apresentados pela maior parte dos sistemas dinâmicos. Existem, no entanto, outros padrões, como por exemplo o equilíbrio e a variação randômica.

9 - Equilíbrio

Alguns sistemas parecem estar em equilíbrio porque as mudanças que os afetam são imperceptíveis de tão lentas ou porque possuem um poderoso feedback negativo que mantém o sistema praticamente constante apesar das mudanças no ambiente. Um exemplo é a força da gravidade que mantém nossos corpos presos à Terra.


UPIS | EAD

Página 16
Módulo 01 - Estrutura e Comportamento de Sistemas Dinâmicos
10 - Variação randômica

Muitas variáveis aparentam comportamentos randômicos. Em muitos casos, o comportamento randômico é a medida de nossa ignorância, aquilo que não conseguimos compreender. Quando alguém diz que há uma variação randômica na demanda de um produto de uma determinada empresa, por exemplo, pode ser que, na realidade, esse alguém desconheça as razões pelas quais isso acontece.

Ninguém pode conhecer todos os motivos pelos quais um cliente decide comprar amanhã quando poderia fazê-lo hoje ou porque uma determinada máquina quebrou agora e não três horas mais tarde.


UPIS | EAD

Página 17
Módulo 01 - Estrutura e Comportamento de Sistemas Dinâmicos

Resumo

A estrutura de feedback de um sistema guia seu comportamento. Muitos sistemas dinâmicos observados no mundo real são exemplos de um conjunto básico de padrões ou modos de comportamento. Três desses modos são fundamentais: crescimento exponencial, busca de um objetivo e oscilação. Cada um desses modos é gerado por uma estrutura específica de feedback. O crescimento exponencial é gerado por um c feedback positivo, a busca de um objetivo é gerado por um feedback negativo e a oscilação é gerada por um feedback negativo com atrasos. Padrões mais complexos como o crescimento em forma de S com ou sem oscilação e o crescimento e colapso resultam de interações não lineares das estruturas de feedback.


UPIS | EAD
Módulo 2

Página 18
Módulo 02 - Construindo modelos simples

1 - Diagramas de Ciclos Causais - DCC vs Diagramas de Fluxos e Estoques - DFE

Os modelos que foram apresentados na Unidade I são denominados Diagramas de Ciclos Causais (ou simplesmente Diagramas de Causas), ou no original em inglês Causal Loop Diagrams. Esses diagramas, apesar de serem muito úteis na representação de sistemas, não mostram as acumulações que ocorrem no mesmo (conhecimento, capital, poder, populações, etc.). Eles recebem esse nome porque cada ligação entre as variáveis representadas tem uma interpretação de causa. Uma seta saindo da variável A em direção à variável B indica que A causa B.

Neste módulo, serão apresentados dois novos elementos que são fundamentais na modelagem de sistemas: os Fluxos e os Estoques.



UPIS | EAD

Página 19
Módulo 02 - Construindo modelos simples
Os DCC - Diagramas de Ciclos Causais - enfatizam a estrutura de feedback de um sistema enquanto os DFE - Diagramas de Fluxos e Estoques - enfatizam a estrutura física do sistema, mostrando os fluxos e acumulações de materiais, dinheiro, informação, etc. Os estoques podem ser as quantidades de um produto, o valor de um débito ou de um crédito, a quantidade de combustível no tanque de um automóvel, ou várias outras coisas sujeitas à acumulação e sobre as quais desejamos obter informações ou controlar.

Os fluxos são as taxas pelas quais os estoques aumentam ou diminuem, como a produção e distribuição de mercadorias, mortes e nascimentos, empréstimo e devolução, investimento e depreciação e vários outros. Os estoques mostram a situação de um sistema em um determinado momento e fornecem as informações nas quais as decisões são baseadas. Essas decisões irão modificar as taxas dos fluxos de um sistema, afetando seus estoques que, por sua vez irão gerar novas informações e assim por diante.


UPIS | EAD

Página 20
Módulo 02 - Construindo modelos simples
2 - Fluxos e Estoques

Qual a diferença entre um estoque e um fluxo? Estoques são acumulações que mostram o estado de um sistema em um determinado momento. Imagine que você está enchendo um copo de água e alguém tire uma foto sua neste momento. O nível da água no copo mostra com exatidão o estado do sistema no momento da tomada da fotografia. O volume de água acumulada é o estoque, que descreve a condição do sistema em um determinado instante do tempo.


UPIS | EAD

Página 21
Módulo 02 - Construindo modelos simples
Uma outra característica dos estoques e que eles não mudam instantaneamente: a mudança ocorre gradualmente durante um período de tempo que varia de sistema para sistema.

As mudanças são provocadas pelos fluxos. Em uma caixa d'água temos dois fluxos: o cano que traz a água (e aumenta o estoque) e o cano que drena a água (e diminui o estoque). Todos os sistemas que mudam através do tempo podem ser representados utilizando-se fluxos e estoques.



O programa de simulação Vensim apresenta as seguintes peculiaridades em relação a dinâmica do estoque:

(1) Sempre é atribuído o valor inicial do estoque no tempo inicial da simulação.

(2) O estoque atualiza os valores do fluxo após um intervalo de tempo;

As premissas (1) e (2) garantem que o estoque só atualiza os fluxos após a 2ª interação, mantendo na 1ª interação o valor inicial. O modelador deve atentar que no último tempo de simulação, o estoque não atualizará todos os valores dos fluxos, pois os fluxos retêm valores em cada intervalo de tempo antes de atualizar o estoque.
Este sistema é semelhante a uma bomba volumétrica, que primeiro enche o pistão com sua capacidade e depois o expele para o reservatório.

Semelhante a uma torneira que acumula água até que tensão superficial reduza formando uma gota de água;

Ou uma máquina a vapor que acumula pressão para realizar trabalho:


UPIS | EAD

Página 22
Módulo 02 - Construindo modelos simples
A seguir encontra-se uma série de variáveis dispostas em linhas. Cada linha representa um determinado sistema. O exercício consiste em identificar, para cada sistema, qual é a variável estoque e quais são as variáveis fluxo. As variáveis estoque são representadas dentro de um retângulo. Observe o exemplo: a população de andorinhas é o estoque que muda em decorrência dos fluxos de mortes ou de nascimentos ao longo do tempo.

  1. Clique sobre a variável que considere ser o estoque, em seguida clique OK.
  2. Se acertar, a variável será envolta em um retângulo. Se errar, você terá uma breve explicação.


UPIS | EAD

Página 23
Módulo 02 - Construindo modelos simples



UPIS | EAD

Página 24
Módulo 02 - Construindo modelos simples



UPIS | EAD

Página 25
Módulo 02 - Construindo modelos simples



UPIS | EAD

Página 26
Módulo 02 - Construindo modelos simples
3 - Identificando os fluxos

Identificar os fluxos é, a princípio, muito simples. Os fluxos que se dirigem ao estoque, de entrada, são representados por uma seta em direção ao estoque e aumentam o mesmo, enquanto os que se dirigem para fora do estoque, de saída, são representados por uma seta saindo do estoque e diminuem o mesmo. Observe o exemplo a seguir:


Os nascimentos aumentam a população de andorinhas enquanto que as mortes diminuem.

Agora, identifique, para os mesmos sistemas do exercício anterior, os fluxos de entrada e os de saída. Para isso, dê um clique em uma das pontas da reta dos fluxos. Na ponta escolhida aparecerá uma seta. Em seguida clique OK.


UPIS | EAD

Página 27
Módulo 02 - Construindo modelos simples



UPIS | EAD

Página 28
Módulo 02 - Construindo modelos simples



UPIS | EAD

Página 29
Módulo 02 - Construindo modelos simples



UPIS | EAD

Página 30
Módulo 02 - Construindo modelos simples
4 - Representando Fluxos e Estoques

A disciplina de Dinâmica de Sistemas, que é a base deste curso, reprsenta fluxos e estoques de acordo com os padrões adotados pelo programa de simulação Vensim:

  • Os estoques são representados por retângulos ( sugerindo uma caixa ou um tanque armazenando os conteúdos do estoque);

Estoques

  • Os fluxos de entrada são representados como "canos" com uma seta na ponta apontando para os estoques;
  • Os fluxos de saída são representados por "canos", com uma seta na ponta, que saem dos estoques (diminuindo-os);

  • As válvulas controlam os fluxos (da mesma forma que as torneiras ou registros controlam o volume de água que entra em um recipiente. Esse conceito será trabalhado nos próximos módulos).

Válvulas (regulam os fluxos)

  • As nuvens representam os limites dos sistemas. Podem ser a origem ou o final de um fluxo que não nos interessa analisar em um determinado momento. (esse conceito será trabalhado nos próximos módulos).

Nuvens



UPIS | EAD

Página 31
Módulo 02 - Construindo modelos simples
A estrutura de todos os diagramas de fluxos e estoques - DFE é composta desses elementos, como demonstrados na figura abaixo:

Vejamos um exemplo baseado no exercício anterior:

A nuvem da esquerda, no modelo acima, significa que não estamos interessados em analisar o fenômeno "Chuvas", não nos interessa de onde elas vêem, porque ocorrem, etc. Simplesmente nos interessa saber que elas afetam positivamente o nível dos reservatórios. Da mesma forma, não estamos interessados em analisar o fenômeno "Consumo de energia", mas sim, como ele afeta negativamente o nível dos reservatórios.

É importante ressaltar que os diagramas não precisam necessariamente serem desenhados nesta posição. Os canos dos fluxos podem fazer "curvas" para que o desenho do diagrama seja mais compreensível, por exemplo.

Para que a compreensão do funcionamento das válvulas seja mais intuitivo, faça o próximo exercício de simulação.


UPIS | EAD

Página 32
Módulo 02 - Construindo modelos simples
5 - Simulando o estoque de água em um tanque

Um tanque, ou ainda, um estoque de água tem dois fluxos: um cano que traz a água até a caixa e um outro que leva a água embora. Se a entrada de água for maior do que a saída, o tanque acabará transbordando (A). Se for o contrário, ele irá esvaziar aos poucos (B). E, se a entrada de água for igual à saída, o nível de água no tanque será mantido (C).


UPIS | EAD

Página 33
Módulo 02 - Construindo modelos simples
É possível prever o comportamento de um sistema com os seguintes dados?
(1) dimensões do tanque = 1metro x 1metro x 1metro = 1m3 = 1000 litros (l)
(2) fluxo de entrada = 20 litros por segundo (l/s)
(3) fluxo de saída = ausente

Se multiplicarmos o volume de água que entrava no tanque pelo tempo podemos dizer, a qualquer momento qual o volume de água no tanque. Por exemplo: em 5 segundos teríamos 100 litros (20 l/s X 5 s), em 10 segundos 200 litros (20 l/s X 10 s), etc. Se em 50 segundos o tanque se enche, isso significa que sua capacidade é de 1.000 litros (20 l/s X 50 s). Além disso, o tanque tem as seguintes dimensões: 1m x 1m x 1m. Ou seja, é um volume de 1 metro cúbico, que equivale a 1000 litros. Isso nos permite fazer outra previsão: o nível de água no tanque em função da altura do tanque. Se em 50 segundos o nível atinge um metro (100 cm), em 25 segundos (metade do tempo) o nível será de 50 cm, em 10 segundos o nível será de 20 cm, ou seja, a cada segundo o nível aumenta em 2 cm (2 cm/s).


UPIS | EAD

Página 34
Módulo 02 - Construindo modelos simples
6 - Integração gráfica

O que acabamos de fazer foi uma integração gráfica, apesar de que, na realidade, não termos desenhado gráfico algum. Podemos fazer isso porque o sistema em questão é muito simples. Muitos outros sistemas da vida real são mais complexos e, portanto, torna-se mais complicado prever seu comportamento. Com a prática, todavia, a utilização de integração gráfica para compreender o funcionamento de muitos sistemas torna-se fácil.

Embora tenhamos acesso a sofisticados programas de computadores que simulam muitos sistemas complexos, é importante que compreendamos e sejamos capazes de prever intuitivamente, por meio da análise gráfica, o comportamento dos sistemas.
Os diagramas de fluxos e estoques só podem ser simulados em computadores. Especificamente, o gráfico ao lado foi feito utilizando-se o Vensim, um programa de computador para fazer simulações que será usado durante esse curso.

A base para sua construção foi o exercício anterior, no qual o tanque foi cheio em 50 segundos. Seu aspecto linear é devido ao fluxo constante (20 l/s) que entra no tanque, o que torna o sistema totalmente previsível. Este gráfico, no entanto, poderia, facilmente, ter sido desenhado à mão.


UPIS | EAD

Página 35
Módulo 02 - Construindo modelos simples
Agora, imagine que haja um atraso de 10 segundos até que o cano que conduz água para o tanque comece a jorrar a mesma quantidade de água do exercício anterior (20 l/s). O gráfico representando essa simulação pode ser visto abaixo. Também bastante simples, não é mesmo?

Em seguida, simule mentalmente a seguinte situação:

  • Entrada de água: 17,7 l/s
  • Saída de água: 12,9 l/s

Após 50 segundos, qual será o volume de água no tanque?

Parece difícil, mas não é.

Basta calcular a entrada líquida de água e multiplicar pelo tempo, ou seja:

Entrada líquida de água = Entrada de água - Saída de água

ou

Entrada líquida de água = 17,7 - 12, 9
Entrada líquida de água = 4,8 litros
                                              segundo

Volume de água no tanque = Entrada líquida de água * Tempo
Volume de água no tanque = 4,8 litros * 50 segundos
                                                    segundo
Volume de água no tanque = 4,8 litros * 50 segundos
                                                    segundo

Volume de água no tanque = 240 litros Por que é importante considerar as unidades na representação de fluxos e estoques?

Os gráficos referentes a essa simulação podem ser observados a seguir:



Um aspecto importante na simulação dinâmica é atribuir corretamente unidades às estruturas do diagrama de fluxos e estoques.

Os fluxos sempre possuem no denominador uma unidade temporal (segundos, dias, ano, etc.)
A simulação dinâmica consiste em avaliar, quantitativamente, o modelo em cada intervalo de tempo.

Portanto os estoques (acumulações do estado de um sistema em um determinado tempo) NÃO APRESENTAM UNIDADES DE TEMPO


UPIS | EAD

Página 36
Módulo 02 - Construindo modelos simples

Lembramos que, caso o fluxo de saída de água fosse maior que o fluxo de entrada de água, não teríamos entrada líquida de água e sim saída líquida de água.


UPIS | EAD

Página 37
Módulo 02 - Construindo modelos simples

Como se pode verificar pelos dois exemplos, os sistemas lineares são relativamente simples de serem interpretados e previsíveis. Mas, como representaríamos esse sistema do tanque, no qual trabalhamos, em um modelo de fluxos e estoques? Veja a figura abaixo.

Muito simples, não é mesmo? Observe agora " ", as válvulas. Veja que elas fazem exatamente o papel das torneiras. Controlam o fluxo de entrada e/ou saída de um estoque. E isso pode ser, como foi dito antes, dinheiro, pessoas, animais, mercadorias, etc. Exatamente porque os sistemas obedecem a padrões de comportamento é que foi possível construir uma representação comum para os mesmos e transformar isso em um programa de computador.


UPIS | EAD

Página 38
Módulo 02 - Construindo modelos simples
Suponha agora que a torneira que controla o fluxo de entrada de água fosse sendo aberta aos poucos (crescimento gradual da vazão), aumentando 1 (um) litro a cada segundo. Em outras palavras, a torneira seria aberta, continuamente, e depois de um segundo estaria jorrando 1 litro de água, com 2 segundos 2 litros, com três segundos três litros e assim pode diante, durante 30 segundos, quando o fluxo de água atingiria 30 litros por segundo.

O gráfico representando o fluxo da entrada de água pode ser observado a seguir. Note que há uma correspondência exata entre os litros e o tempo em segundos, que pode ser melhor observado aos 10, 20 e 30 segundos.

Vamos ver como ficou o gráfico representando o crescimento do estoque (volume) de água?


UPIS | EAD

Página 39
Módulo 02 - Construindo modelos simples
Isso mesmo. O crescimento linear do fluxo de entrada de água provocou um crescimento exponencial no estoque de água(observação: o volume reduzido nos 3 segundos iniciais são imperceptíveis devido a escala do eixo Y dividida a cada 150 litros). No primeiro gráfico, o de entrada de água, a área representada pelo retângulo ABC é igual ao volume de água contida no tanque após os 30 segundos (450 litros, no caso). Em outras palavras, o volume de água contido no tanque é uma integração do fluxo de entrada de água. O cálculo dessa área é muito importante para estudar o comportamento dos estoques nos sistemas.


Para calcular a área de um triângulo retângulo utilizamos a seguinte fórmula:

Área = base x altura / 2

Então, observando o gráfico

Temos no eixo X 30 segundos (base) e no eixo Y 30 litros por segundo (altura):

                                                  litros
               30 segundos * 30 —————
                                                segundo
Área = —————————————————
                                      2

Área = 30 * 30 litros / 2 = 900 litros / 2

O que implica que:

Área = 450 litros

ou seja, exatamente a quantidade de água que temos no tanque após 30 segundos, coerente com a metodologia de cálculo integral.

Calculo errado para o volume do tanque:
Soma da progressão aritmética = 1+2+3+4+...+27+28+29+30 = 465 litros



UPIS | EAD

Página 40
Módulo 02 - Construindo modelos simples

7 - Integrando os fluxos de entrada e saída

As convenções do Diagrama de Fluxos e Estoques (criadas por Jay Forrester em 1961) foram baseadas nessa metáfora dos fluxos de água e do tanque. De fato, a quantidade de água no tanque em um determinado momento é o resultado da acumulação da água que entrou menos a que saiu (assumindo que não houve evaporação). Da mesma forma, a quantidade de mercadorias em um armazém é o resultado da acumulação das entradas e saídas de mercadorias. Como foi observado, os estoques e os fluxos têm um significado matemático preciso. Os estoques acumulam ou integram seus fluxos: o resultado líquido da taxa de entrada menos a de saída é a alteração que o estoque vai sofrer. Isso corresponde exatamente à seguinte integral:

O Fluxo de entrada(s) representa o valor da entrada no tempo s, situado entre o tempo inicial to e tempo atual t. De modo equivalente, a taxa líquida de mudança de um estoque é derivativa, definida pela seguinte equação:

d(Estoque)/dt = Fluxo de entrada(t) - Fluxo de saída(t)

A notação tradicional utilizada para cálculos, em especial no Vensim, é mostrada a seguir:

Essa equação é equivalente à integral apresentada e representa o conceito de que os estoques acumulam seus fluxos de entrada e saída, começando com um valor de estoque to, ou seja, seu valor inicial. No caso dos exemplos que foram apresentados, todos começaram com estoque inicial igual a zero.

É importante ressaltar que o foco de nosso curso é a modelagem e simulação de negócios, mas necessitamos construir uma base de conhecimentos sobre a qual assentaremos nossos futuros trabalhos. Mesmo não calculando as equações derivadas e integrais, uma vez que o programa de computador foi feito para isso, é importante ter uma idéia do tipo de cálculo utilizado nas simulações e, também, para compreender o que é uma simulação computadorizada. Lembramos que a análise gráfica é um requisito essencial para a compreensão dos padrões de comportamento dos sistemas e nos próximos módulos abordaremos essa questão com maior profundidade.


UPIS | EAD

Página 41
Módulo 02 - Construindo modelos simples

8 - Modelando e construindo as fórmulas

Vamos rever dois dos exercícios que fizemos no início desse módulo, reconstruí-los com os símbolos da modelagem e construir as fórmulas para solucioná-los, incluindo as unidades. Para isso, cada um deles será acompanhado de um enunciado, como se fosse um problema real que tivéssemos de solucionar por meio de simulação. Eles serão acompanhados de gráficos.

1. Quinhentas andorinhas vivem próximas a duas rodovias. Todos os anos nascem 100 andorinhas. Porém, todos os anos, 120 andorinhas morrem por morte natural ou atropelada. Quantas andorinhas estarão vivendo nesta área daqui a 10 anos?

Primeiro, vamos converter o modelo rascunhado abaixo:

no modelo padrão:

Em seguida, vamos construir as fórmulas:

População de andorinhas = INTEGRAL (100-120,500)
Unidades: andorinhas
Comentário: a população inicial de andorinhas é de 500 andorinhas

Nascimentos = 100
Unidades: andorinhas/ano
Comentário: 100 andorinhas nascem todos os anos

Mortes = 120
Unidades: andorinhas/ano
Comentário: 120 andorinhas morrem todos os anos


UPIS | EAD

Página 42
Módulo 02 - Construindo modelos simples
Essas fórmulas estariam prontas para serem digitadas em computador e realizar várias simulações, como por exemplo: Daqui a vinte e cinco anos, quantas andorinhas existirão? E se nascerem 115, quantas existirão daqui a vinte anos? E assim por diante. Posteriormente, poderemos observar que o Vensim constrói parte da integral automaticamente e, é claro, realiza todos os cálculos necessários.
Observe o gráfico que é a resposta para a questão colocada:

Mantidas as condições iniciais, em 10 anos a população de andorinhas irá decrescer de 500 para 300 indivíduos.

Este é um exemplo clássico de uma taxa de crescimento negativa. Porém, algumas dúvidas podem surgir. Se a população de andorinhas fica menor com o passar do tempo, como é que o número de andorinhas que nasce permanece o mesmo? Os casais que restarem terão mais filhotes para compensar a morte dos outros? Se existem menos andorinhas, não era de se esperar que o número de mortes também diminuísse? A resposta é que este é um exercício simplificado e, portanto, um pouco distante da realidade. À medida que o curso avança iremos sofisticando os modelos, a fim de representar sistemas mais complexos.


fluxo líquido = 100 – 120 = - 20 andorinhas / ano

Estoque = fluxo líquido * tempo

                  - 20 andorinhas
Estoque = ————————— * 10 anos
                          ano

Estoque = - 20 andorinhas * 10 = -200 andorinhas
Estoque final = Estoque inicial + Estoque
Estoque final = 500 – 200 = 300 andorinhas


UPIS | EAD

Página 43
Módulo 02 - Construindo modelos simples
2. Existem, atualmente, aproximadamente cinco milhões árvores em uma floresta. Uma madeireira vem derrubando aproximadamente 100.000 árvores por ano. Grupos ambientais, preocupados com a possibilidade da floresta ser totalmente destruída, têm trabalhado muito, plantando aproximadamente 33.000 árvores todos os anos. Quantas árvores existirão na floresta daqui a trinta anos?

Rascunho:

Modelo padrão:

Observe que o modelo pode ser construído tanto para um lado como para o outro. O importante é a coerência na direção dos fluxos.


UPIS | EAD

Página 44
Módulo 02 - Construindo modelos simples
Fórmulas:

Floresta = INTEGRAL(33000-100000,5000000)
Unidades: árvores
Comentário: a população inicial de árvores é de 5.000.000 de árvores

Replantio = 33000
Unidades: árvores/ano
Comentário: 33.000 árvores são plantadas todos os anos

Desmatamento = 100000
Unidades: árvores/ano
Comentário: 100.000 árvores são derrubadas todos os anos

Dentro de 30 anos a floresta terá aproximadamente 2 milhões de árvores a menos, apesar do esforço dos ambientalistas.


fluxo líquido = 33000 – 100.000 = - 67.000 arvore / ano
Estoque = fluxo líquido * tempo
                 - 67.000 árvores
Estoque = ————————— * 30 anos
                          ano
Estoque = - 67.000 árvores * 30 = -2.010.000 árvores
Estoque final = Estoque inicial + Estoque
Estoque final = 5.000.000 – 2.010.000 = 2.990.000 árvores


UPIS | EAD

Página 45
Módulo 02 - Construindo modelos simples
Resumo

Neste módulo aprendemos as diferenças entre os Diagramas de Ciclos Causais e os Diagramas de Fluxos e Estoques. Vimos que os primeiros são importantes para mostrar as influências e ligações entre as variáveis de um sistema, enquanto que o segundo apresenta o estado do sistema em um determinado momento, mostrando os fluxos e acumulações de materiais, dinheiro, informação, etc.

Um segundo passo foi aprender a diferenciar o que é estoque e o que é fluxo em um sistema. Também foi demonstrado como representar graficamente os fluxos e estoques. Aprendemos que as válvulas controlam a entrada e saída dos fluxos e que as nuvens representam os limites do sistema, ou seja, delimitam o que estamos interessados em estudar e analisar.

Na prática, observamos como a água se acumula e um tanque e que essa acumulação pode ser calculada matematicamente por meio de uma integral. Vimos que também podemos integrar graficamente, utilizando esse aprendizado para prever o comportamento dos sistemas. Finalmente, vimos como determinar as fórmulas para os modelos.


UPIS | EAD

Página 46
Módulo 02 - Construindo diagramas de fluxos e estoques
1 - Construindo um Diagrama

Os Diagramas de Fluxos e Estoques (ou de Taxas e Níveis) são meios para se representar a estrutura de um sistema geralmente com dados quantitativos, diferindo do diagrama de ciclos causais(geralmente qualitativos). Os Estoques são fundamentais para gerar e analisar o comportamento de um sistema. Os Fluxos provocam mudanças nos estoques. Os Diagramas de Fluxos e Estoques são importantes na construção de um modelo de simulação porque ajudam a definir que tipos de variáveis são importantes no comportamento do sistema. Neste módulo, será construído um diagrama que descreve os relacionamentos entre a publicidade de um produto e a quantidade de clientes existentes e potenciais.

Excepcionalmente, neste módulo, demonstraremos os recursos de diagrama dos fluxos e estoques sem incluir dados quantitativos.

  • Inicie o Vensim.

  • Clique no ícone New Model (ou execute o comando File>New Model...).

  • Clique OK na caixa de diálogo Model Settings para aceitar os valores padrão (default).

  • Clique no ícone Save na barra de ferramentas. Escolha uma pasta e salve o modelo como clientes ou outro nome de sua escolha.


UPIS | EAD

Página 47
Módulo 02 - Construindo diagramas de fluxos e estoques
2 - Inserindo Estoques (Level)

Estoques são também conhecidos como níveis, acumulações ou variáveis de estado (state variables). Os estoques mudam seus valores constantemente, com o passar do tempo. Os fluxos (Rates) são os responsáveis pelas mudanças nos valores dos estoques. Por sua vez, os estoques de um sistema determinam os valores dos fluxos. Conceitos intermediários ou cálculos são conhecidos como variáveis auxiliares e, como os fluxos, podem mudar instantaneamente.

Quando da construção de um diagrama de fluxos e estoques, deve-se analisar que variáveis acumulam valores com o passar do tempo. Uma outra maneira de pensar sobre isso é: se o tempo fosse reduzido a zero no seu sistema, que variáveis ainda permaneceriam com valor retido? Por exemplo, imagine um sistema no qual você coloca água em um copo. A água contida no copo é o estoque. Se o tempo é congelado, o fluxo (a água sendo colocada no copo) se interrompe, mas seria possível observar uma dada quantidade de água no copo (o estoque). Uma vez que tenham sido identificados os estoques do sistema, eles são inseridos no diagrama e, em seguida, faz-se as conexões com os fluxos e variáveis auxiliares.


Dica: A construção de modelos tende a ser interativa, portanto não espere (ou tente) construir tudo correto da primeira vez, sempre será possível alterar o diagrama posteriormente.

Vamos iniciar a construção do modelo.

  • Selecione a ferramenta Box Variable e clique uma vez sobre o diagrama. Digite Clientes Potenciais e pressione Enter.

  • Com a ferramenta Box Variable ainda selecionada, clique uma vez no diagrama aproximadamente 7 cm à direita de Clientes Potenciais. Digite Clientes e pressione Enter.


UPIS | EAD

Página 48
Módulo 02 - Construindo diagramas de fluxos e estoques
Para criar fluxos, é necessário que você:
  • Selecione a ferramenta Rate. Clique uma vez sobre Clientes Potenciais e então mova o cursor sobre Clientes e clique novamente. Aparece uma caixa de texto. Digite novos clientes e pressione Enter.

Atenção: sempre digite o nome (identificador) na caixa de texto após diagramar o fluxo. Se for pressionada a tecla “Esc” ou o botão do mouse fora da caixa de texto, o fluxo é representado sem identificador.

O fluxo tem uma ponta de seta simples, indicando a direção em que o material pode fluir (o Fluxo pode apenas aumentar o Estoque). Observe que isto é apenas um diagrama.

Em um modelo de simulação, as equações governam a direção em que o material pode fluir.


Atente também para o fato de que o padrão estabelecido para a ferramenta Rate pode ser modificado para fazer com que ela apresente duas pontas de seta (indicando duas direções).


UPIS | EAD

Página 49
Módulo 02 - Construindo diagramas de fluxos e estoques
Para construir o fluxo que vai de Clientes até Clientes Potenciais e fazer com que o diagrama tenha aproximadamente o formato do exemplo, siga as instruções passo a passo.

Instrução para diagramação.


Clique uma vez sobre Clientes, pressione e mantenha pressionada a tecla Shift enquanto move o cursor, aproximadamente 1 cm à direita de Clientes, e clique novamente.
  • Continue pressionando a tecla Shift para os próximos cliques.
  • Mova o cursor para baixo, em linha reta, aproximadamente 3,5 cm (abaixo e à direita de Clientes), e então clique novamente.
  • Mova o cursor para a esquerda, aproximadamente 2,5 cm abaixo e à esquerda de Clientes Potenciais, e clique uma vez.
  • Mova o cursor para cima e à esquerda de Clientes Potenciais e clique uma vez.
  • Mova o cursor sobre Clientes Potenciais e dê outro clique.
  • Solte a tecla Shift. Aparece uma caixa de texto. Digite o nome do fluxo: perdendo clientes e pressione Enter.


UPIS | EAD

Página 50
Módulo 02 - Construindo diagramas de fluxos e estoques
3 - Inserindo Variáveis Auxiliares e Setas

Para inserir as variáveis auxiliares e as setas, siga as instruções logo a seguir, de modo que seu diagrama fique aproximadamente como o apresentado.

Instrução para diagramação.


  • Selecione a ferramenta Variable. Clique uma vez à esquerda e abaixo de novos clientes e digite tempo para tornar-se cliente e pressione Enter.
  • Clique uma vez à direita e abaixo de perdendo cliente, digite vida do produto e pressione Enter.
  • Selecione a ferramenta Arrow. Clique sobre Clientes Potenciais e, em seguida, no espaço em branco acima e entre as variáveis Clientes Potenciais e novos clientes. Depois, clique sobre a válvula anexada a novos clientes.

Uma seta curva irá unir o estoque e a válvula do fluxo. O Vensim permite que se conecte a seta ao nome do fluxo ou à válvula. Estruturalmente, não faz nenhuma diferença.

  • Clique uma vez em tempo para tornar-se cliente e então sobre o nome do fluxo novos clientes.
  • Clique uma vez em Clientes e, em seguida, na válvula anexada ao fluxo perdendo clientes.
  • Clique uma vez sobre vida do produto e, em seguida, sobre o nome do fluxo perdendo clientes.


UPIS | EAD

Página 51
Módulo 02 - Construindo diagramas de fluxos e estoques
4 - Compondo a Estrutura

Vamos adicionar mais variáveis ao modelo. Ao terminar seu diagrama, estará parecido com o apresentado. Para isso, siga as instruções.

Instrução para diagramação.


Selecione a ferramenta Box Variable e clique uma vez no diagrama, aproximadamente 5 cm acima do estoque Clientes Potenciais.

  • Digite Popularidade e tecle Enter.
  • Selecione a ferramenta Rate. Clique uma vez no espaço vazio do diagrama, aproximadamente 5 cm à esquerda do estoque Popularidade.
  • Mova o cursor sobre Popularidade e clique uma vez sobre este estoque.
  • Digite ganhando popularidade na caixa de texto do nome fluxo e tecle Enter.

Um fluxo denominado ganhando popularidade será construído entre o estoque e uma nuvem. A nuvem define os limites do modelo: não devemos nos preocupar de onde vem o material ou o que acontece com o mesmo quando vai para uma nuvem.

  • Clique uma vez no estoque Popularidade. Mova o cursor para a parte vazia do diagrama, aproximadamente 5 cm à direita de Popularidade e clique outra vez. Digite na caixa de texto do nome do fluxo esquecendo a marca e tecle Enter.
  • Selecione a ferramenta Variable. Clique, no diagrama, abaixo e à esquerda do fluxo ganhando popularidade e digite eficiência da publicidade, mas não tecle Enter (deixe a caixa de texto aberta).
  • Clique novamente no diagrama, logo abaixo de eficiência da publicidade, e digite orientação ao cliente.
  • Clique novamente no diagrama, logo abaixo do fluxo esquecendo a marca, e digite tempo para esquecer.

Observe que é possível entrar com múltiplas variáveis no diagrama sem teclar Enter.

  • Clique novamente no diagrama, entre Popularidade e novos clientes, e digite efeito da popularidade nos novos clientes e tecle Enter.
Se o espaço for insuficiente, é possível reposicionar toda a estrutura do modelo na página.
  • Execute o comando Edit>Select All (ou tecle Ctrl + A) e mova a estrutura para o lugar que achar mais conveniente na página (não é possível fazer isso com a ferramenta Lock selecionada. Se for o caso, selecione a ferramenta Move/Size).
  • Clique fora da estrutura para desmarcar a seleção.


UPIS | EAD

Página 52
Módulo 02 - Construindo diagramas de fluxos e estoques

Vamos continuar construindo o modelo. Ao terminar seu diagrama, deverá estar parecido com o apresentado. Para isso continue seguindo as instruções.

 

  • Selecione a ferramenta Arrow. Clique uma vez sobre eficiência da publicidade e, em seguida, sobre ganhando popularidade.
  • Clique uma vez sobre orientação ao cliente e, em seguida, sobre ganhando popularidade.
  • Clique uma vez sobre Popularidade, em seguida, sobre o espaço vazio acima e entre Popularidade e esquecendo a marca e depois sobre a válvula anexada a esquecendo a marca.
  • Clique uma vez sobre tempo para esquecer e depois sobre a válvula anexada a esquecendo a marca.
  • Clique uma vez sobre Popularidade e, em seguida, sobre efeito da popularidade nos novos clientes.
  • Clique uma vez sobre efeito da popularidade nos novos clientes e, em seguida, sobre a válvula anexada a novos clientes.
  • Clique uma vez sobre clientes e, em seguida, no espaço vazio do diagrama um pouco acima da nuvem do fluxo esquecendo a marca e, então, sobre ganhando popularidade.
  • Reorganize as variáveis e as setas do diagrama utilizando a ferramenta Move/Size.


UPIS | EAD

Página 53
Módulo 02 - Construindo diagramas de fluxos e estoques
5 - Customizando Diagramas

Os diagramas podem ser customizados de diferentes maneiras. O procedimento padrão para diagramas do Vensim é mostrar estoques como caixas, com o respectivo nome dentro da mesma. Fluxos são mostrados com o nome na válvula, embora algumas vezes um fluxo não tenha nome. Variáveis auxiliares, constantes, variáveis externas, etc., são mostrados com um simples nome, sem caixas ou outras figuras geométricas. Essa seção descreve algumas opções para a customização de diagramas.

Opções do diagrama:

  • Selecione a ferramenta Move/Size. Clique no handle do estoque Popularidade (pequeno círculo no canto inferior direito da caixa) e arraste-o até que a caixa fique um pouco maior.
  • Clique uma vez sobre o estoque Clientes Potenciais para selecioná-lo, pressione (e mantenha pressionada) a tecla Shift, clique uma vez sobre Clientes e também sobre Popularidade. Execute o comando Layout>Size to LastSel.
  • Execute o comando Edit>Select all (ou Ctrl + A). Clique no ícone para seleção de cores na Barra de Status (este ícone pode ser encontrado passando o ponteiro do mouse sobre os mesmos até que a expressão "set color on selected arrows" apareça). Escolha uma cor (vermelho, por exemplo) e então clique em um espaço vazio do diagrama.


UPIS | EAD

Página 54
Módulo 02 - Construindo diagramas de fluxos e estoques
Observe que tanto as setas como os fluxos são alterados. No caso de alterar setas e fluxos separadamente, é necessário selecionar cada um individualmente (ex.: selecione todos os fluxos e então escolha uma cor. Repita o mesmo para as setas).
  • Clique sobre Popularidade e pressione a tecla Shift enquanto clica em Clientes Potenciais e Clientes. Na barra de status, clique em b para selecionar negrito (ele se transforma em B) e mude a cor das variáveis e da caixa (por meio dos ícones localizados na Barra de Status).
  • Tecle Esc ou a tecla correspondente ao nº. 1 no teclado para seleção da ferramenta Lock (ou clique no ícone correspondente).
  • Utilizando o comando View>Zoom>200% terá o diagrama apresentado no dobro do tamanho.
  • Execute o comando View>Zoom>100%, o diagrama retorna ao seu tamanho original. A ferramenta Zoom apenas mostra seu diagrama em diferentes tamanhos.


UPIS | EAD

Página 55
Módulo 02 - Construindo diagramas de fluxos e estoques

Parabéns! Ao final deste módulo você já conheceu os principais recursos para diagramar modelos dinâmicos. Que tal divulgar seu modelo no fórum indicando qual recurso despertou-lhe interesse? Apreciarei sua iniciativa em compartilhar o crescimento do seu aprendizado.

 


UPIS | EAD

Página 56
Módulo 02 - Construindo diagramas de fluxos e estoques

Resumo

Este módulo descreveu a construção de um diagrama de fluxos e estoques, relacionando a publicidade de um produto e a quantidade de clientes existentes e potenciais. O conceito central foi a influência da popularidade da marca sobre os novos clientes.

Foram realizadas as seguintes atividades, relacionadas ao uso do Vensim:

  • Uso da ferramenta Box Variable para criação de variáveis do tipo estoque.
  • Uso da ferramenta Rate para criação de variáveis do tipo fluxo.
  • Utilização da tecla Shift em conjunto com o mouse para "flexionar os canos" das variáveis fluxo.
  • Inserção de variáveis auxiliares e setas de ligação.
  • Utilização do comando Edit>Select All para selecionar todo o diagrama.
  • Utilização do comando Layout>Size to LastSel para dimensionar as variáveis de acordo com o tamanho da última variável.
  • Utilização da tecla Shift e do mouse para selecionar múltiplas variáveis.

Utilização da ferramenta Zoom para visualizar o diagrama.


UPIS | EAD
Módulo 1

Página 57
Módulo 01 - O processo de modelagem
1 - Modelagem

Serão abordadas as principais características do processo de modelagem. É importante que se tenha um conceito objetivo do que e para que modelar.

Devemos, antes de tudo, compreender que a modelagem e a simulação de sistemas é uma ferramenta que pode nos auxiliar no mundo dos negócios, quer estejamos atuando como gerente ou como empresário, na solução de muitos problemas complexos.

A modelagem, como parte de um processo de aprendizagem, é interativa, um processo contínuo de formulação de hipóteses, testes e revisão. O objetivo é, em suma, solucionar problemas. Não raras vezes, isso acontece com criatividade e inovação.


UPIS | EAD

Página 58
Módulo 01 - O processo de modelagem
O objetivo da modelagem: gerentes como designers de organizações

O cientista e criador da disciplina Sistemas Dinâmicos, Jay Forrester, gosta de fazer a seguinte pergunta:

Qual é a pessoa mais importante nas operações de segurança de um avião?

A maioria das pessoas responde: - São os pilotos! Na verdade, as pessoas mais importantes são os designers (projetistas, em um conceito amplo). Habilidosos e bem treinados, os pilotos são críticos na segurança de uma aeronave.

Porém muito mais importante é projetar um avião estável, que seja robusto sob condições adversas e que mesmo pilotos comuns possam pilotá-los, estejam sob stress, cansados ou expostos a situações de risco.



UPIS | EAD

Página 59
Módulo 01 - O processo de modelagem
Existem gerentes que tomam decisões (quem contratar, que preços estabelecer, quando lançar um novo produto, etc.) e existem os gerentes designers, que dão forma às estruturas das organizações, formulam estratégias e criam regras para auxiliar no processo decisório.

Apesar de mais importantes, os gerentes designers chamam menos a atenção. Muitos gerentes, principalmente altos executivos, gastam muito tempo agindo como pilotos - tomando decisões e controlando os subordinados - mais do que criando uma estrutura organizacional consistente com sua visão e valores.

Gerentes que procuram aumentar suas habilidades de design atuam na base da tentativa e erro ou pela imitação de outros.

O "mundo virtual" da modelagem e simulação é uma importante ferramenta para os gerentes, tanto na área operacional quanto no desenho de suas organizações.


UPIS | EAD

Página 60
Módulo 01 - O processo de modelagem
2 - O Cliente e o Modelador

Modelar não é uma atividade isolada, ela está inserida no contexto social da organização. Assim, antes que o processo de modelagem se inicie, o modelador deve ter acesso à organização e identificar quem é o seu cliente.

O cliente não é a pessoa que lhe contratou ou a pessoa que lhe paga para fazer os modelos, embora seja bom tê-los por perto e em alta conta. Seus clientes são as pessoas que deverão ser influenciadas para que seu trabalho tenha impacto.

São as pessoas cujo comportamento deve ser mudado para solucionar um problema. Ele pode ser um CEO ou uma máquina da linha de produção. Clientes podem ser indivíduos, grupos ou comunidades inteiras.

Os clientes de um estudo de modelagem podem ser seus colegas de faculdade, pessoas comuns ou você mesmo. O nosso foco, contudo, são os projetos para organizações.


Chief Executive Officer - a pessoa que tem o cargo executivo mais alto de uma organização.


UPIS | EAD

Página 61
Módulo 01 - O processo de modelagem
Para ser efetivo, o processo de modelagem deve ser focado nas necessidades dos clientes. Porém, não raras vezes, esses clientes estão muito ocupados, envolvidos com as políticas da organização.

Podem estar preocupados com suas carreiras ou concentrados na solução de um problema. Possivelmente, eles não irão prestar muita atenção na "elegância" de sua teoria ou na "inteligência" de seu modelo.

Modelar é uma tarefa para ajudar o cliente; não para trazer benefícios ao modelador. O ambiente real em que o cliente está inserido determina a natureza do modelo, e o processo de modelagem deve ser coerente com as habilidades, capacidades e objetivos dos clientes.

O objetivo é ajudá-los a solucionarem os problemas deles. Se os clientes perceberem que seu modelo não está orientado às necessidades, não ficarão interessados, e seu trabalho terá pouco impacto.


UPIS | EAD

Página 62
Módulo 01 - O processo de modelagem
Não queremos com isso afirmar que, ao focar o cliente, o modelador deva fazer o que o cliente quer. Não se deve concordar de imediato a pedidos para incluir isso, detalhar aquilo ou priorizar um processo em relação a outros.

Um bom processo de modelagem muda a concepção do cliente em relação a seus problemas. Modeladores têm a obrigação de exigir que seus clientes justifiquem suas opiniões, convertam suas idéias em dados e aceitem novos pontos de vista.


UPIS | EAD

Página 63
Módulo 01 - O processo de modelagem
Infelizmente, muitos clientes não estão interessados em aprender, mas apenas em usar os modelos para justificar suas conclusões e utilizá-los como instrumentos de poder dentro das organizações. Como modelador, sua obrigação é conduzir seu trabalho com ética, integridade e rigor.

É necessário ter a coragem de dizer aos seus clientes que "suas mais convictas crenças estão erradas", se o processo de modelagem comprovar isso. Se um cliente pedir para que construa um modelo para comprovar algo que ele deseja, mas que contraria as análises ou a ética, recuse.

Se não for possível convencer seu cliente a usar a modelagem honestamente, é melhor abandoná-lo e procurar um cliente melhor.


UPIS | EAD

Página 64
Módulo 01 - O processo de modelagem
3 - Modelagem e Interatividade

Na prática, a primeira tarefa é contatar quem acredita que a modelagem é uma ferramenta e pode ser útil na solução de um problema real.

Seu contato inicial não precisa ser necessariamente com o cliente (e, às vezes, é melhor que não seja), mas com um cliente gatekeeper que possa introduzi-lo ao cliente.


Pessoa da organização, geralmente muito bem informada e relacionada internamente, que cumpre papéis importantes, como, por exemplo, reunir pessoas com interesses comuns para resolver um problema ou desenvolver um projeto em conjunto.


UPIS | EAD

Página 65
Módulo 01 - O processo de modelagem
A principal dúvida que surge então é:

- Como desenvolver um modelo que seja útil para meus clientes?

Não existe um livro de receitas para modelos de sucesso. Não existe nenhum procedimento que garanta que um modelo vá ser útil.

Modelar é algo inerentemente criativo. Cada indivíduo tem diferentes estilos e abordagens. Contudo, modeladores de sucesso seguem um processo disciplinado que envolve as seguintes atividades:

1. identificação e articulação do problema e determinação de seus limites;
2. formulação de uma hipótese dinâmica ou teoria sobre as causas do problema;
3. construção de um modelo para testar a hipótese dinâmica;
4. teste do modelo para verificar se ele atende aos objetivos;
5. projetar e avaliar políticas de melhoria.


UPIS | EAD

Página 66
Módulo 01 - O processo de modelagem
Antes de detalhar cada uma das atividades, é importante contextualizar o processo de modelagem em relação às atividades das pessoas. A modelagem é um processo constante de retroalimentação e não uma seqüência linear de passos. Modelos são construídos sob intensa interatividade, questionamento contínuo, testes e refinamento.

A figura a seguir representa o processo de modelagem como um ciclo interativo. O objetivo inicial determina os limites e o escopo dos processos de modelagem, mas o que é aprendido durante o processo alimenta e altera nossa compreensão inicial do problema e, às vezes, os próprios objetivos.

Mas o mais importante de tudo é que a modelagem está inserida no amplo ciclo de aprendizagem das organizações. Pilotos entram em um simulador de vôo e aprendem mais rapidamente, efetivamente e de modo seguro como operar uma aeronave e então utilizam essas habilidades no mundo real. A experiência que adquirem no mundo real retorna aos laboratórios e é utilizada para construir simuladores ainda melhores. O mesmo pode e deve acontecer com os gerentes nas organizações.


UPIS | EAD

Página 67
Módulo 01 - O processo de modelagem
A figura mostra que os modelos de simulação são alimentados pelas informações de nossos modelos mentais e pelas informações que retornam do mundo real.

Estratégias, estruturas e regras de decisão do mundo real podem ser representadas e testadas no mundo virtual dos modelos. Os experimentos e testes conduzidos no modelo retroalimentam e alteram nossos modelos mentais e nos levam a criar novas estratégias, estruturas e regras de decisão.

Essas novas políticas são, então, implementadas no mundo real, levando a inovações e melhorias, e alimentam, mais uma vez, nossos modelos mentais e de simulação.


UPIS | EAD

Página 68
Módulo 01 - O processo de modelagem
4 - Identificação e Articulação do Problema

A fase mais importante da modelagem é a identificação e articulação do problema. Em que fato o cliente está mais interessado? Que problema ele está tentando resolver? Qual é o real problema? Qual é o objetivo do modelo?

Um objetivo claro é um ingrediente muito importante para o sucesso da modelagem. Tenha cuidado com um analista que proponha modelar todo um negócio ou um sistema social em vez de um problema.

Cada modelo é a representação de um sistema - um grupo de funcionalidades inter-relacionadas formando um todo complexo. Mas um modelo para ser útil precisa estar orientado a um problema específico de modo simples e não tentar ser como um espelho detalhado de um sistema real.

Von Clausewitz formulou uma frase que resume essa idéia: "o mapa não é o território". E completamos: um mapa tão detalhado como o território possivelmente não terá uso.


UPIS | EAD

Página 69
Módulo 01 - O processo de modelagem
A arte de modelar é a arte de conhecer o que cortar, modelando com a faca do cérebro. Isso permite decidir o que pode ser ignorado de modo que apenas as características que atendam aos nossos objetivos permaneçam.

Usualmente, o modelador desenvolve a análise do problema por meio de discussões com o cliente e sua equipe, complementando com pesquisa em arquivos e bases de dados, entrevistas, observação direta ou participação. Nesta fase o modelador deve construir um diagrama de ciclos causais para avaliar a dinâmica do problema.

Posteriormente devemos desenvolver nossos modelos referenciais, literalmente, como um conjunto de gráficos e outros dados descritivos, mostrando a evolução do problema ao longo do tempo. Eles ajudam a quebrar visão de curto prazo que muitas pessoas têm.

Faça isso junto com o cliente, determinando um horizonte de tempo e definindo aquelas variáveis e conceitos que considerem importantes para compreender o problema.


UPIS | EAD

Página 70
Módulo 01 - O processo de modelagem
A definição do horizonte de tempo do passado deve se estender o suficiente para mostrar como o problema surgiu e descrever os seus sintomas. Deve se estender o suficiente no futuro para poder capturar os efeitos retardados e indiretos de potenciais políticas adotadas. Muitas pessoas subestimam o tempo de reação dos sistemas e definem horizontes de tempo muito curtos.

A principal deficiência de nossos modelos mentais é nossa tendência em pensar em causa e efeito como algo local e imediato.

Em sistemas dinâmicos complexos, causa e feito estão distantes no tempo e no espaço. Trabalhe com seus clientes, pensando sobre possíveis reações às políticas a serem implementadas e até em que horizonte de tempo elas podem se manifestar.

Um horizonte de tempo longo é um antídoto a uma visão de mundo orientada a eventos isolados contraria a habilidade de identificar padrões de comportamento e as estruturas de comportamento que as geram.


UPIS | EAD

Página 71
Módulo 01 - O processo de modelagem
5 - Formulação de uma Hipótese Dinâmica

Uma vez que o problema tenha sido identificado e caracterizado dentro de horizonte de tempo apropriado, os modeladores devem começar a desenvolver uma teoria chama de hipótese dinâmica, para compreender o comportamento problemático do sistema.

A hipótese é dinâmica porque deve contemplar uma explicação da dinâmica que caracteriza o problema, delineando a estrutura de feedback e de estoques e fluxos do sistema.

É uma hipótese porque é sempre provisória, sujeita a revisões ou abandono à medida que se aprende com o processo de modelagem do mundo real. Na prática, a discussão do problema com o cliente e membros da equipe é uma conversa confusa.

Cada membro da equipe tem uma teoria diferente sobre a origem do problema e é necessário tomar conhecimento delas e capturá-las. Muitas vezes, o objetivo do modelo é resolver um problema crítico que persiste há anos e causa sérios conflitos entre os membros da equipe.

Cada um tenta advogar suas posições e enfraquecer a dos demais membros do grupo. Desde o início, o modelador precisa agir como um facilitador, capturando esses modelos mentais sem criticá-los ou filtrá-los. Muitas técnicas auxiliam nessa fase, e o objetivo é ajudar o cliente a desenvolver uma explicação endógena (interna) para o problema.


UPIS | EAD

Página 72
Módulo 01 - O processo de modelagem
Os sistemas dinâmicos procuram explicações endógenas para os fenômenos. Uma teoria endógena é gerada pela dinâmica de um sistema por meio da interação entre as variáveis e agentes representados no modelo. Podemos explorar os padrões de comportamento do modelo criado, alterando sua estrutura e suas regras.

Já uma teoria exógena (que vem de fora dos limites do sistema) explica o comportamento de algumas variáveis do sistema em função de outras variáveis cujo comportamento tivemos que assumir antecipadamente.

O foco em explicações endógenas dos sistemas não significa que não podemos incluir variáveis exógenas em nossos modelos. Mas devemos questionar se esta variável exógena participa de um feedback importante para os elementos endógenos. Se isso for verdade, os limites do sistema poderão ser expandidos, e a variável passar a ser tratada como uma variável endógena.


UPIS | EAD

Página 73
Módulo 01 - O processo de modelagem
Mapeando a estrutura do sistema: os Sistemas Dinâmicos contemplam uma variedade de ferramentas que ajudam a definir os limites de um sistema e sua estrutura causal. Entre essas, temos os diagramas de limites do modelo, os diagramas de subsistemas, os diagrama de ciclos causais e os mapas de fluxos e estoques.

Diagramas de limites do modelo: esse diagrama resume o escopo do modelo, listando quais são as principais variáveis endógenas, as exógenas e as que não serão contempladas no modelo (excluídas). Um exemplo é mostrado abaixo a partir de um modelo genérico para analisar os feedbacks entre o sistema de energia e a economia.

Endógenas
Exógenas
Excluídas
PIB População Estoques
Consumo Mudanças tecnológicas Comércio internacional
Investimento Impostos Políticas ambientais
Poupança Política energética Fontes não-energéticas
Preços   Combustíveis substitutos
Salários   Distribuição uniforme
Taxa de inflação    
Desemprego    
Taxa de juros    
Produção de energia    
Demanda de energia    
Etc.    


UPIS | EAD

Página 74
Módulo 01 - O processo de modelagem
Diagramas de subsistemas: mostram a arquitetura geral de um modelo por meio dos fluxos de materiais, dinheiro, mercadorias e informação entre dois subsistemas. Subsistemas podem ser organizações como a empresa e o cliente ou subunidades organizacionais como produção, marketing e desenvolvimento de produtos.

Esses diagramas mostram os limites e níveis de agregação dos diferentes tipos de organizações ou agentes envolvidos. Também disponibilizam alguma informação sobre variáveis exógenas. Um modelo simples é representado na figura abaixo:

Os Diagramas de ciclos causais são mapas simples mostrando as ligações entre as variáveis em termos de causas e efeitos.
Os Mapas de fluxos e estoques ou Diagramas de Fluxos e Estoques, enfatizam a estrutura física do sistema.


UPIS | EAD

Página 75
Módulo 01 - O processo de modelagem
6 - Teste de um Modelo

Uma vez que tenhamos desenvolvido a hipótese dinâmica, definido os limites do modelo e criado o modelo conceitual, devemos testá-lo. Algumas vezes, podemos testar a hipótese dinâmica diretamente por meio de dados ou experimentos no modelo real.

Porém, em muitas situações, especialmente quando tratamos de sistemas humanos, é difícil, perigoso, antiético ou mesmo impossível realizar experimentos no mundo real para testar a hipótese dinâmica.

Nesses casos (e na maioria das vezes), deveremos conduzir esses experimentos no mundo virtual. Para isso, teremos que converter o reino conceitual dos diagramas para um modelo formal e completo, com equações, parâmetros e condições iniciais.


UPIS | EAD

Página 76
Módulo 01 - O processo de modelagem
Formalizar um modelo conceitual gera importantes insigths mesmo antes que ele esteja pronto para ser simulado. A formalização nos obriga a reconhecer conceitos vagos e a resolver contradições que não foram percebidas durante a fase conceitual.

Nesse momento, ocorre o teste de nossa real compreensão do problema: computadores não aceitam pura retórica. Pelo contrário, somos obrigados a escrever equações e estimar parâmetros durante a modelagem no computador.

Os testes se iniciam a partir do momento em que escrevemos a primeira equação. Parte do teste é, naturalmente, comparar o comportamento do modelo com o comportamento atual do sistema.

Mas testar envolve muito mais do que a replicação de comportamentos. Cada variável deve corresponder a um conceito significativo do mundo real. Cada equação deve ser verificada em termos de sua consistência dimensional (para não somarmos maçãs com laranjas).



UPIS | EAD

Página 77
Módulo 01 - O processo de modelagem
Modelos devem ser testados sob condições extremas, inclusive aquelas nunca observadas no mundo real. O que acontecerá com o PIB de uma economia moderna se repentinamente reduzirmos as fontes de energia a zero?

O que acontecerá com uma montadora de automóveis se multiplicarmos o preço dos automóveis por mil? E se aumentarmos os estoques dos distribuidores de automóveis em 1.000%?

Embora essas condições jamais tenham sido observadas no mundo real, não há dúvida de que o comportamento do sistema deverá ser: sem energia, o PIB deverá cair para próximo de zero; com o preço dos carros mil vezes maior, a demanda deverá cair para zero; com estoques tão altos, a produção deverá cair para zero.



UPIS | EAD

Página 78
Módulo 01 - O processo de modelagem
Muitas vezes, imaginamos que um modelo jamais falharia em um teste como esse. Contudo, muitos modelos computadorizados largamente utilizados em economia, psicologia, administração e outras disciplinas falham e violam leis da física, embora sejam capazes de simular comportamentos com eficiência.

Esses testes extremos, juntamente com os outros testes de comportamento do modelo, são ferramentas úteis para descobrirem falhas nos modelos e melhorar seu desempenho.


UPIS | EAD

Página 79
Módulo 01 - O processo de modelagem
Uma vez que o cliente tenha adquirido confiança na estrutura e comportamento do modelo, podemos elaborar e avaliar políticas de melhoria.

Elaborar políticas de melhoria é muito mais do que mudar os valores dos parâmetros do modelo. Trata-se de incluir novas estratégias, estruturas e regras de decisão.

Uma vez que o feedback da estrutura de um sistema determina sua dinâmica, grande parte do tempo irá envolver a mudança dos feedbacks dominantes.

Isso implica redesenhar a estrutura de fluxos e estoques, eliminar atrasos, mudar o fluxo e a qualidade da informação disponível nos pontos-chave de decisão, ou, fundamentalmente, reinventar o processo de decisão dos atores que atuam no sistema.


UPIS | EAD

Página 80
Módulo 01 - O processo de modelagem
Resumo

O módulo aborda as principais características do processo de modelagem.

A modelagem e simulação de sistemas é uma ferramenta que pode nos auxiliar no mundo dos negócios. O objetivo é, em suma, solucionar problemas.

O objetivo da modelagem: gerentes como designers de organizações

Existem gerentes que tomam decisões (quem contratar, que preços estabelecer, quando lançar um novo produto, etc.) e existem os gerentes designers, que dão forma às estruturas das organizações, formulam estratégias e criam regras para auxiliar no processo decisório.

Modelar não é uma atividade isolada, ela está inserida no contexto social da organização. O nosso foco, contudo, são os projetos para organizações.

Na prática, a primeira tarefa é contatar quem acredita na modelagem, como uma ferramenta que pode ser útil na solução de um problema real. Modeladores de sucesso seguem um processo disciplinado que envolve as seguintes atividades:

1. identificação e articulação do problema e determinação de seus limites;
2. formulação de uma hipótese dinâmica ou teoria sobre as causas do problema;
3. construção de um modelo para testar a hipótese dinâmica;
4. teste do modelo para verificar se ele atende aos objetivos;
5. projetar e avaliar políticas de melhoria.

Estratégias, estruturas e regras de decisão, utilizadas no mundo real, podem ser representadas e testadas no mundo virtual dos modelos. Os experimentos e testes conduzidos no modelo retroalimentam e alteram nossos modelos mentais e nos levam a criar novas estratégias, estruturas e regras de decisão.

A fase mais importante da modelagem é a identificação e articulação do problema. Um objetivo claro é um ingrediente muito importante para o sucesso da modelagem.

Usualmente, o modelador desenvolve a análise do problema por meio de discussões com o cliente e sua equipe, complementando com pesquisa em arquivos e bases de dados, entrevistas, observação direta ou participação.