Módulo 1 - Desconto Simples

Página 1

1 - Conceitos Gerais

Em seu dia-a-dia, as empresas efetuam operações de compra e venda de mercadorias e serviços, assumindo obrigações e direitos financeiros que podem ser representados por fluxos de desembolsos e recebimentos de caixa. Fatores, que, geralmente, ocorrem de maneira “descasada”, ou seja, muitas vezes a empresa necessita de recursos imediatos para a liquidação de obrigações com terceiros, mas dispõem apenas de direitos de recebimentos futuros, decorrentes da venda de produtos a prazo. Para fazer face às necessidades imediatas, a companhia pode utilizar uma das operações mais comuns no mercado: a operação de desconto.

Basicamente, essa operação se caracteriza pela antecipação do recebimento de direitos futuros (recebíveis), mediante sua entrega a uma instituição financeira. Assim, necessitando de recursos para suprir necessidades de caixa, a empresa entrega ao banco seus recebíveis (duplicatas, faturas de cartão de crédito, cheques pré-datados etc.), decorrentes de vendas a prazo, recebendo, em troca, a antecipação desses valores.

Página 2

Módulo 1 - Desconto Simples

Com a finalidade de obter ganho com a operação, os bancos retiram sua remuneração do valor nominal dos títulos, creditando às empresa o chamado “valor líquido ou descontado”.

Por exemplo:

Situação atual:

Uma empresa necessita de R$ 10 mil para pagar obrigações que vencem hoje, mas somente irá dispor deste volume de recursos daqui a 30 dias, quando deverá receber R$ 11 mil devido às vendas a prazo.

Página 3

Módulo 1 - Desconto Simples

Operação de Desconto:

Com a finalidade de obter os recursos de que necessita e cumprir com suas obrigações financeiras, a empresa entrega os recebíveis a um banco que antecipa o montante, descontando do valor a sua remuneração. Supondo que o desconto foi de R$ 1 mil, a empresa recebe R$ 10 mil e liquida suas dívidas.

O Banco, que desembolsou R$ 10 mil na operação, fica com os títulos e recebe os R$ 11 mil dos clientes da empresa, quando estes fizerem a liquidação da dívida, na data de vencimento dos títulos.

Observação: nesse tipo de operação, caso os clientes não paguem, os valores são debitados da conta da empresa, ou seja, os bancos não assumem o risco de crédito dos clientes da companhia.

Página 4

Módulo 1 - Desconto Simples

2 - Tipos de Desconto
Conforme podemos verificar, as operações de desconto podem ser realizadas tanto com base no regime de juros simples como no de juros compostos, existindo dois tipos de desconto para cada um desses regimes: o desconto “por dentro”(ou racional) e o desconto “por fora” (bancário ou comercial).

Página 5

Módulo 1 - Desconto Simples

De forma genérica o valor descontado ou valor líquido (V), a ser creditado na conta da empresa, é a diferença entre o valor nominal (original) do título (N) e o desconto (D), este último representando a remuneração do banco.
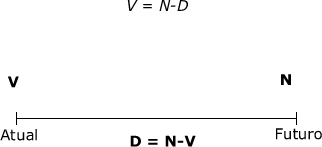	(1)
Resolvendo a equação (1) para o desconto (D), pode-se concluir que o valor do desconto será dado pela diferença entre o valor nominal (N) e o valor descontado (V).
D = N-V	(2)

Página 6

Módulo 1 - Desconto Simples

3 - Desconto Simples Racional ou “por dentro” Incorpora os conceitos e relações básicas de juros simples. Nesse tipo de desconto, o valor descontado (Vr) é o valor nominal do título trazido a valor presente pelo conceito de juros simples, ou seja:
	(3)
A equação (3) revela que o valor descontado no desconto racional (Vr) é encontrado mediante a divisão do valor nominal (N) por um mais a taxa de desconto (i) multiplicada pelo prazo de antecipação (n). Note que, a não ser pela denominação das variáveis, cujas letras foram alteradas para representar de maneira mais próxima os conceitos utilizados pelo mercado neste tipo de operação, se substituirmos (Vr) por (PV) e N por (FV) teremos, na verdade, a fórmula de valor presente para o RCS, estudada no módulo II. Para acharmos a fórmula do desconto, retornamos à fórmula geral, onde: D = N – V e, considerando Dr como valor do desconto e Vr como sendo o valor descontado, ambos no desconto racional, substituindo-os na equação, teremos:
Dr = N - Vr	(4)
Como Vr é dado por:
	(3)
Substituindo a equação (3) na (4) e resolvendo a expressão, obteremos:
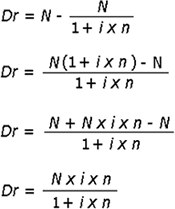	(5)
Aplicando-se a equação (5), em operações de desconto racional, acharemos o valor do desconto (Dr). Exercícios Resolvidos

Página 7

Módulo 1 - Desconto Simples

1) Uma empresa possui uma duplicata de valor nominal igual a R$ 10.000,00, vencível em três meses. Sabendo-se que a taxa de desconto simples (racional) é de 3,4% ao mês, determine: a) o valor descontado e b) o valor do desconto.

Para entendermos melhor a operação, digamos que a empresa do exemplo, necessitando de recursos, foi até um banco e efetuou uma operação de desconto. Nesta operação, ela entregou uma duplicata no valor de R$ 10.000,00, que vence daqui a 3 meses, ao banco que, por sua vez, antecipou R$ 9.074,41(valor descontado) à empresa. A diferença, R$ 925,59 (valor do desconto), é a parcela que irá ficar com o banco quando o cliente da empresa liquidar a dívida e resgatar o título.

Título de crédito nominativo que representa e comprova uma operação a ser paga pelo devedor.

Página 8

Módulo 1 - Desconto Simples

2) Seja um título de valor nominal de R$ 5.000,00 vencível em um ano, que está sendo liquidado 5 meses antes de seu vencimento. Sendo de 42% ao ano a taxa de juros atual do mercado, pede-se calcular o valor do desconto e o valor descontado da operação.

Importante: Embora útil na determinação do “preço justo”, em transações sob regime de capitalização simples, o desconto racional praticamente não é usado no mercado financeiro. Na prática, a metodologia empregada é a do desconto simples comercial, bancário ou “por fora”, demonstrada a seguir.

Página 9

Módulo 1 - Desconto Simples

4 - Desconto Simples Comercial, Bancário ou “por fora”

Amplamente adotado pelo mercado em operações de crédito bancário e comercial a curto prazo, nesta modalidade a taxa de desconto (d) incide diretamente sobre o valor nominal do título, ou seja:

Dc=N x d x n

(6)

Sendo:
Dc = valor do desconto comercial
N = valor nominal do título
d = taxa de desconto comercial
n = prazo de antecipação

A equação (6) nos diz que em operações de desconto simples, comercial, bancário ou “por fora”, o valor do desconto será calculado mediante a aplicação da taxa de desconto (d) e do prazo de antecipação (n), diretamente no valor nominal do título (N).

Página 10

Módulo 1 - Desconto Simples

Substituindo-se a equação (6) na equação geral do valor descontado, onde V = N – D, e considerando Vc como o valor descontado e Dc o valor do desconto, ambos no desconto comercial, teremos:

VC = N - Dc

(7)

Substituindo a fórmula (6) Dc = N x d x n na equação (7) e resolvendo a expressão, obteremos:

VC = N - N x d x n	(8)
VC = N(1-d x n)

A equação (8) é utilizada para o cálculo do valor descontado (Vc) no desconto simples bancário, comercial ou “por fora”.

Exercícios Resolvidos

Página 11

Módulo 1 - Desconto Simples

Repetindo os enunciados 1 e 2, para o desconto comercial simples, teremos:

3) Uma empresa possui uma duplicata de valor nominal igual a R$ 10.000,00, vencível em três meses. Sabendo-se que a taxa de desconto simples (comercial) é de 3,4% ao mês, determine: a) o valor descontado e b) o valor do desconto.

Variáveis	Solução
	a) Valor Descontado	b) Valor do desconto
N = 10.000	Vc = N ( 1- d x n )	Dc = N x d x n
n = 3 m
d = 0,034	Vc = 10.000( 1- 0,034 x 3 )	Dc = 10.000 x 0,034 x 3
Vc = ?
Dc = ?	Vc = R$ 8.980,00	Dc = R$ 1.020,00

4) Seja um título de valor nominal de R$ 5.000,00 vencível em um ano, que está sendo liquidado 5 meses antes de seu vencimento. Sendo de 42% ao ano a taxa de juros atual do mercado, pede-se calcular o valor do desconto e o valor descontado da operação.

Variáveis	Solução
	a) Valor Descontado	b) Valor do desconto
N= 5.000	Vc=N(1-d x n)	Dc=N x d x n
n=5m	Vc=5.000(1-0,035 x 5)	Dc=5.000 x 0,035 x 5
d=0,035
Vc=?
Dc=?	Vc=R$ 4.125,00	Dc=R$ 875,00

Observação! Por incidir sobre o valor nominal o desconto simples comercial proporciona maior volume de encargos financeiros em comparação ao desconto simples racional.

Este é o tipo de desconto utilizado pelas empresas e bancos no dia a dia

Página 12

Módulo 1 - Desconto Simples

5 - Despesas Bancárias

Em operações de desconto com bancos são geralmente cobradas taxas adicionais com a finalidade de cobrir despesas administrativas e operacionais.

Essas taxas, aqui representadas pela letra “t”, incidem diretamente sobre o valor nominal do título, no momento da efetivação do desconto. Dessa maneira, pode-se concluir que o valor do desconto comercial, acrescido da taxa, o qual chamaremos de (Dc’) será de:

Dc'=(N x d x n) + (t x N)

(9)

A equação (9) calcula o valor do desconto simples comercial com cobrança de taxa administrativa. Simplificando a equação teremos:

Dc'=N(d x n + t)

(10)

A partir da equação genérica, onde: V = N – D, poderemos definir a fórmula do valor descontado para operações com taxa de administração, onde:

Vc'=N-Dc'

Vc'=N - N(d x n + t)

Vc'=N[1-(d x n + t)]

(11)

A equação (11) é a expressão de cálculo do valor descontado em operações com cobrança de taxa administrativa (Vc’).

Exemplo de operações envolvendo taxas administrativas e operacionais

Página 13

Módulo 1 - Desconto Simples

5) Uma duplicata de valor nominal de R$ 60.000,00 é descontada num banco dois meses antes de seu vencimento. Sendo de 2,8% ao mês a taxa de desconto usada na operação, calcular o desconto e o valor descontado. Sabe-se ainda que o banco cobra 1,5% sobre o valor nominal do título, descontados integralmente no momento da liberação dos recursos, como despesa administrativa.

Página 14

Módulo 1 - Desconto Simples

6 - Utilizando o Excel

1. Abra uma pasta nova que depois poderá ser arquivada com o nome de Desconto Simples.

PLANILHA DE CÁLCULO PARA DESCONTO SIMPLES RACIONAL OU “POR DENTRO”

2. No intervalo B2 escreva: Desconto Racional ou "por dentro".

3. No intervalo B3:D3, digite os títulos “Variáveis”, “Dados” e “Resultado”.

4. No intervalo B4:B8, indique as variáveis “Valor Nominal”, “Desconto”, “Taxa”; “Prazo” e “Valor Descontado”.

5. Usando os recursos de formatação do Excel, formate os intervalos C4:D5 e C8:D8 como moeda e C6:D6 como percentual %, todos com duas casas decimais.

6. No intervalo D4:D8 registre as fórmulas de cálculo das variáveis “Valor Nominal”, “Desconto”, “Taxa”; “Prazo” e “Valor Descontado”, utilizando a função lógica SE, ou então digite:

6.1 Na célula D4: =SE(C4="?";C5*(1+C6*C7)/(C6*C7);"")
6.2 Na célula D5: =SE(C5="?";C4*C6*C7/(1+C6*C7);"")
6.3 Na célula D6: =SE(C6="?";C5/(C7*(C4-C5));"")
6.4 Na célula D7: =SE(C7="?";C5/(C6*(C4-C5));"")
6.5 Na célula D8: =SE(C4="?";D4-C5;SE(C5="?";C4-D5;C4-C5))

7. As fórmulas acima estabelecem as relações lógicas da função. Analisando, por exemplo, a equação da célula D4, teremos:

SE for cumprida a condição lógica C4 = “?”

ENTÃO calcule C5*(1+C6*C7)/(C6*C7) e apresente o resultado na célula D4

SENÃO registre um rótulo vazio “” na célula D4

8. Caso deseje utilizar a função SE diretamente, coloque o cursor na célula D4 e selecione INSERIR, FUNÇÃO.

9. No campo CATEGORIA escolha: LÓGICA e no campo NOME escolha SE.

10. Tomando como base a equação 6.1, no campo Teste lógico insira C4=”?”; no campo Valor_se_verdadeiro, digite: C5*(1+C6*C7)/(C6*C7) e no campo Valor_se_falso digite “”.

11. Ao final da digitação clique OK.

12. Repita os procedimentos de 8 a 11 para o intervalo de D5:D8, com base nas equações 6.2 a 6.5.

Página 15

Módulo 1 - Desconto Simples

PLANILHA DE CÁLCULO PARA DESCONTO SIMPLES BANCÁRIO, COMERCIAL OU “POR FORA”

13. No intervalo B10 escreva: Desconto Comercial, Bancário ou "por fora".

14. No intervalo B11:D11, digite os títulos “Variáveis”, “Dados” e “Resultado”.

15. No intervalo B12:B16, indique as variáveis “Valor Nominal”, “Desconto”, “Taxa”; “Prazo” e “Valor Descontado”.

16. Usando os recursos de formatação do Excel, formate os intervalos C12:D13 e C16:D16 como moeda e C14:D14 como percentual %, todos com duas casas decimais.

17. No intervalo D12:D16 registre as fórmulas de cálculo das variáveis “Valor Nominal”, “Desconto”, “Taxa”; “Prazo” e “Valor Descontado”, utilizando a função lógica SE, ou então digite:

17.1 Na célula D12: =SE(C12="?";C13/(C14*C15);"")
17.2 Na célula D13: =SE(C13="?";C12*C14*C15;"")
17.3 Na célula D14: =SE(C14="?";C13/(C15*C12);"")
17.4 Na célula D15: =SE(C15="?";C13/(C14*C12);"")
17.5 Na célula D16:=SE(C12="?";D12-C13;SE(C13="?";C12-D13;C12-C13))

Efetue a solução dos exercícios resolvidos no capítulo colocando as variáveis do enunciado nos campos referentes aos “dados” e “?” no campo “dados” da variável que se deseja calcular no problema, “Valor Nominal” ou “Desconto”. Nesta planilha o “Valor descontado é calculado automaticamente, colocando-se “?” no campo “dados” do “Valor Nominal” ou “Desconto”.

Lembre-se que, independente do tipo de desconto, a unidade de tempo da taxa deve ser a mesma da operação. Caso necessite converter a taxa para outro prazo, utilize o conceito de taxas proporcionais por se tratar de “desconto simples”.

As figuras abaixo representam as planilhas construídas mediante os procedimentos descritos anteriormente:

Página 16

Módulo 1 - Desconto Simples

Resumo

Com o objetivo de suprir necessidades de caixa, muitas empresas realizam operações de desconto de recebíveis junto a instituições financeiras.

Nesse tipo de operação, a companhia antecipa o recebimento de valores futuros, decorrentes de vendas a prazo, mediante a entrega dos chamados recebíveis (duplicatas, cheques pré-datados, faturas de cartão de crédito etc.) a uma instituição financeira que, em contrapartida, desconta destes valores sua remuneração e credita na conta da empresa o valor líquido ou descontado, representado pelo valor original dos recebíveis, menos o desconto.

No regime de capitalização simples existem dois tipos de desconto:

1) desconto simples racional ou “por dentro”; e

2) desconto comercial, bancário ou “por fora”.

O desconto simples comercial, bancário ou “por fora” é o desconto empregado em operações de curto prazo no mercado. As equações utilizadas nestas operações são:

Dc=N x d x n (6)

Vc=N(1-d x n) (8)

Mediante o uso da equação (6) calculamos o valor do desconto (Dc), que representa a parcela de remuneração dos bancos neste tipo de operação.

A fórmula (8) é utilizada para calcular o valor líquido (Vc) que será depositado na conta da empresa, já deduzido do desconto.

Caso haja a cobrança de taxa de administração ou custos operacionais, sobre o montante da operação, as fórmulas que deverão ser utilizadas serão: Vc'=N[1-(d x n + t)] e Dc'=N(d x n + t).

No que se refere ao desconto racional ou “por dentro”, as fórmulas de cálculo do valor líquido ou descontado (Vr) e do desconto (Dr) são, respectivamente:

Vr= N e Dr = N x i x n .
1 + i x n 1 + i x n

Embora o desconto racional seja o mais “justo” em termos matemáticos, por representar a aplicação do conceito do RCS, este não é empregado no mercado financeiro, servindo apenas como referência teórica.

Página 17

Módulo 1 - Desconto Simples

A equação de cálculo do valor descontado e do valor do desconto, tanto para o composto “por dentro”, quanto para o composto “por fora”, são apresentadas a seguir:

	(1)
	(2)
	(3)
	(4)

As equações (1) e (2), respectivamente, aplicam-se ao cálculo do valor descontado (Vrc) e do valor do desconto (Drc), em operações do composto “por dentro”.

As equações (3) e (4) são utilizadas, respectivamente, para o cálculo do valor descontado (Vcc) e do valor do desconto (Dcc), em operações do composto “por fora”.

como ocorre no desconto simples, podem ser classificados em: composto “por fora” e composto “por dentro”.

Ao contrário do desconto simples, no qual as operações existentes no mercado são efetuadas sob o conceito daquele “por dentro”, no desconto composto, as operações baseiam-se na metodologia do “por fora”.

Por ser construído com base na aplicação direta das relações próprias ao regime de juros compostos, a taxa de juros das operações de desconto composto “por fora” representam as taxas efetivas negociadas no mercado, não necessitando, portanto, de conversão, a fim de que sejam passíveis de comparação com outros tipos de operações.

Página 18

Módulo 2 - Taxa implícita em operações de desconto simples comercial

1 - Operações de Desconto

Verificamos que as operações de desconto efetuadas pelo mercado são realizadas sob o conceito do chamado desconto simples comercial, bancário ou “por fora”.

Uma das características desse tipo de operação, observada na equação de cálculo do valor do desconto (Dc = N x d x n) é a de que a taxa da operação “d” é empregada sobre o valor nominal dos recebíveis (N), gerando um custo maior para as empresas em relação ao racional.

Sem entrar na discussão do modelo utilizado pelo mercado, que se constitui em prática usual, é importante verificarmos que as taxas divulgadas pelas instituições financeiras para operações de desconto não representam efetivamente o custo destas operações, servindo apenas como referencial para o cálculo do valor descontado e do valor do desconto, especificamente para este tipo de operação.

Para entendermos melhor esta questão, vamos analisar o exemplo 3, resolvido no módulo anterior, no qual uma duplicata de valor nominal de R$ 10.000,00, foi descontada três meses antes de seu vencimento, a uma taxa de desconto comercial de 3,4%.

Aplicando a equação de cálculo do valor descontado (Vc = N (1 – d x n)), chegaremos a um valor de R$ 8.980,00, que representa a quantia que a empresa receberá, pela antecipação de seus recebíveis, no momento da contratação da operação apropriada.

Tecnicamente, utilizando-nos dos conceitos de capitalização, ao aplicarmos a taxa de desconto (3,4%) sobre o valor descontado (R$ 8.980,00) deveríamos encontrar o valor nominal ou futuro de R$ 10.000,00.

Conforme poderemos verificar a seguir, isto não ocorre, evidenciando a existência de uma taxa de juros implícita superior à de desconto informada.

Página 19

Módulo 2 - Taxa implícita em operações de desconto simples comercial

2 - Evidências da taxa implícita pelo RCS

Continuando nosso raciocínio, vamos primeiramente relembrar a equação que serve para a capitalização de valores pelo RCS, onde:

FV = PV (1 + i x n)

(1)

Considerando que, em operações de desconto simples comercial, FV = N, PV = Vc e i = d, se substituirmos estas variáveis na equação (1) teremos:

N = Vc (1 + d x n)

(2)

Aplicando a equação (2) no fluxo abaixo, representativo da questão resolvida no início do módulo, obteríamos um valor nominal (ou futuro) de apenas R$ 9.895,96:

Analisando-se esse resultado podemos concluir que:

1) a taxa de desconto não representa a taxa de juros da operação porque, quando aplicada aos R$ 8.980,00, por três meses, não resulta em R$ 10.000,00.

2) a taxa de juros implícita na operação é maior do que a taxa de desconto informada, pois necessitamos de uma taxa maior do que a taxa de desconto informada de 3,4% a.m. para, ao capitalizar os R$ 8.980,00, pelo prazo de três meses, chegarmos aos R$ 10.000,00.

Página 20

Módulo 2 - Taxa implícita em operações de desconto simples comercial

3 - Evidências da Taxa Implícita pelo RCC

Partindo-se do mesmo raciocínio aplicado para o RCS, vamos relembrar a equação que serve para a capitalização de valores pelo RCC, onde:

Fv=PV(1+i)ⁿ

(3)

Sendo: FV = N, PV = Vc e i = d, substituindo-se estas variáveis na equação (3) teremos:

N=Vc(1+d)ⁿ

(4)

Aplicando a equação (4) no fluxo sob análise, obteríamos um valor nominal (ou futuro) de apenas R$ 9.927,46:

Mais uma vez, agora pelo RCC, podemos concluir que:

1) a taxa de desconto não representa a taxa de juros da operação;

2) a taxa de juros implícita na operação é maior do que a taxa de desconto informada.

Cálculo da Taxa Implícita - Após verificarmos que a taxa de desconto não representa a de juros embutida na operação, seja no RCS ou no RCC, surge-nos, então, a necessidade de a determinarmos, a fim de sabermos qual o custo efetivo das operações de desconto.

Página 21

Módulo 2 - Taxa implícita em operações de desconto simples comercial

4 - Conversão para o RCS

Por definição, a taxa de juros (i), implícita em operações de desconto, será aquela que, aplicada sobre o valor descontado (Vc), pelo período de antecipação (n), promove a equivalência financeira entre este valor (Vc) e o valor Nominal (N), obedecendo o regime de capitalização escolhido. Em termos matemáticos, teremos, para o RCS:

Vc (1 + i x n) = N

(5)

Sabendo-se que, no desconto simples comercial o valor descontado é dado por: Vc = N(1 - d x n), substituindo Vc na equação (5) e resolvendo para “ i ”, obteremos:

N(1 - d x n)(1 + i x n) = N

(1 + i x n) = N
N(1-d x n)

i x n = 1 -1
(1-d x n)

i x n = d x n -1
(1-d x n)

i = d
(1-d x n)

(6)

A equação (6) indica que a taxa de juros simples, embutida em operações de desconto simples comercial, será encontrada mediante a divisão da taxa de desconto (d) por “um” menos a taxa de desconto multiplicada pelo período de antecipação (n).

Página 22

Módulo 2 - Taxa implícita em operações de desconto simples comercial

Aplicando a fórmula (6)

em nosso exemplo, onde d = 3,4% a.m. e n = 3, encontraremos:

i= 0,034 =3,786192% a.m.
(1-0,034x3)

O resultado de 3,786192% representa a taxa de juros simples da operação, que pode ser confirmada no fluxo abaixo.

A figura acima comprova que, sendo a taxa de desconto simples comercial (d) de 3,4% ao mês e o prazo de antecipação (n) de três meses, a taxa de juros implícita na operação será de 3,786192%, ou seja, o custo da empresa, pelo RCS, será de 3,786192%.

Esta é a taxa que, aplicada ao valor descontado (Vc), pelo prazo de três meses, faz com que este chegue ao valor nominal do título (N).

Página 23

Módulo 2 - Taxa implícita em operações de desconto simples comercial

5 - Conversão para o RCC

Sendo a taxa de juros implícita em operações de desconto (i) aquela que promove a equivalência financeira entre o valor descontado (Vc) e o valor Nominal (N). Para o RCC teremos:

N=Vc(1+d)ⁿ

(7)

Sabendo-se que, no desconto simples comercial o valor descontado é dado por: Vc=N(1-d x n), substituindo Vc na equação (7) e resolvendo para “ i ”, obteremos:

(8)

A equação (8) indica como calcular a taxa de juros compostos, embutidas em operações de desconto simples comercial (d), a partir dela própria e o prazo de antecipação (n).

Página 24

Módulo 2 - Taxa implícita em operações de desconto simples comercial

Aplicando a fórmula (8), onde: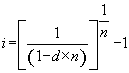

, em nosso exemplo, cuja taxa (d) é de 3,4% e o prazo (n) igual a 3, encontraremos:

O resultado de 3,651253% representa a taxa de juros composto da operação (juros efetivos), que pode ser confirmada ao analisarmos o fluxo a seguir:

A figura acima comprova que, sendo a taxa de desconto simples comercial (d) de 3,4% ao mês, e o prazo de antecipação (n) igual a 3, a taxa de juros compostos implícita na operação será de 3,651253%, ou seja, o custo da empresa, pelo RCC, será de 3,651253% a.m., pois esta é aquela que, pelo RCC, leva os R$ 8.980,00 para R$ 10.000,00 após 3 meses.

Exercícios resolvidos

Página 25

Módulo 2 - Taxa implícita em operações de desconto simples comercial

1) Qual a taxa de juros, simples e composto, implícita em uma operação de desconto efetuada pelo prazo de 4 meses a uma taxa de 4,8% a.m.?

a) taxa de juros simples:

Variaveis:	Solução
i = ?
d = 0,048 a.m.
n = 4m	i = 5,94% a.m.

b) taxa de juros composto

Variaveis:	Solução
i = ?
d = 0,048 a.m.
n = 4m	i = 5,47% a.m.

Resposta: A taxa de juros implícita na operação, pelo RCS, será de 5,94% a.m. e, pelo RCC, 5,47% a.m..

2) Um administrador recebe a informação de que a taxa de desconto cobrada pelas instituições financeiras está em 4,5% a.m., enquanto a taxa de operações de empréstimo é de 4,7% a.m.. Com base nestas informações e, sabendo que a empresa necessita recursos pelo prazo de 3 meses, qual será a operação mais vantajosa em termos de custo?

Transformando a taxa de desconto na taxa efetiva, para fins de comparação com a taxa de empréstimo, obtêm-se:

Variaveis:	Solução
i = ?
d = 0,045 a.m.
n = 3 m	i = 4,95% a.m.

Sendo de 4,95% a.m. a taxa efetiva (juros compostos) correspondente a taxa de desconto de 4,5% a.m., é mais vantajoso para a empresa efetuar uma operação de empréstimo, cujo custo efetivo é menor (4,7% a.m.).

Como podemos observar, o conhecimento da metodologia de transformação das taxas de desconto em taxas efetivas (juros compostos) são de grande importância ao administrador de empresas, na medida em que, somente mediante a sua conversão, poderemos compará-las as taxas de desconto simples comercial com outras taxas praticadas no mercado.

Página 26

Módulo 2 - Taxa implícita em operações de desconto simples comercial

5 - Utilizando o Excel

1. Abra uma pasta nova que depois poderá ser arquivada com o nome de “Desconto Simples Comercial – Taxa implícita”.

PLANILHA DE CÁLCULO PARA CONVERSÃO DE TAXAS DE DESCONTO SIMPLES COMERCIAL EM JUROS SIMPLES

2. No intervalo B2 escreva: Conversão da taxa de desconto para juros simples.

3. No intervalo B3:D3, digite os títulos “Variáveis”, “Dados” e “Resultado”.

4. No intervalo B4:B6, indique as variáveis “Taxa de desconto”, “Prazo” e “Taxa de juros”.

5. Usando os recursos de formatação do Excel, formate os intervalos C4:D4 e C6:D6 como percentual %, todos com duas casas decimais.

6. Nas células D4 e D6 registre as fórmulas de cálculo das variáveis “Taxa de desconto” e “Taxa de juros”, utilizando a função lógica SE, ou então digite:

6.1 Na célula D4: =SE(C4="?";C6/(1+C6*C5);"")
6.2 Na célula D6: =SE(C6="?";C4/(1-C4*C5);"")

7. As fórmulas acima estabelecem as relações lógicas da função. Analisando, por exemplo, a equação da célula D4, teremos:

SE for cumprida a condição lógica C4 = “?”

ENTÃO calcule C6/(1+C6*C5) e apresente o resultado na célula D4

SENÃO registre um rótulo vazio “” na célula D4

8. Caso deseje utilizar a função SE diretamente, coloque o cursor na célula D4 e selecione INSERIR, FUNÇÃO.

9. No campo CATEGORIA escolha: LÓGICA e no campo NOME escolha SE.

10. Tomando como base a equação 6.1, no campo Teste lógico insira C4=”?”; no campo Valor_se_verdadeiro, digite: C6/(1+C6*C5) e no campo Valor_se_falso digite “”.

11. Ao final da digitação clique OK.

12. Repita os procedimentos de 8 a 11 para o intervalo D6, com base na equação 6.2.

Página 27

Módulo 2 - Taxa implícita em operações de desconto simples comercial

PLANILHA DE CÁLCULO PARA CONVERSÃO DE TAXAS DE DESCONTO SIMPLES COMERCIAL EM JUROS COMPOSTOS (EFETIVOS)

13. No intervalo B8 escreva: Conversão da taxa de desconto para juros compostos.

14. No intervalo B9:D9, digite os títulos “Variáveis”, “Dados” e “Resultado”.

15. No intervalo B10:B12, indique as variáveis “Taxa de desconto”, “Prazo” e “Taxa de juros”.

16. Usando os recursos de formatação do Excel, formate os intervalos C10:D10 e C12:D12 como percentual %, todos com duas casas decimais.

17. Nos intervalos D10 e D12 registre as fórmulas de cálculo das variáveis “Taxa de desconto” e “Taxa de juros”, utilizando a função lógica SE, ou então digite:

17.1 Na célula D10: =SE(C10="?";-(1-(1+C12)^C11)/((1+C12)^C11*C11);"")
17.2 Na célula D12: =SE(C12="?";(1/(1-C10*C11))^(1/C11)-1;"")

Página 28

Módulo 2 - Taxa implícita em operações de desconto simples comercial

As figuras abaixo representam as planilhas construídas mediante os procedimentos descritos anteriormente:

Página 29

Módulo 2 - Taxa implícita em operações de desconto simples comercial

Resumo

Verificamos neste módulo que as taxas de desconto simples comercial, também denominado de bancário ou “por fora”, não representam a de juros da operação, seja no Regime de Capitalização Simples (RCS), ou no Regime de Capitalização Composto (RCC).

Essa característica faz com que aquelas divulgadas pelas instituições financeiras, para este tipo de operação, não possam ser diretamente comparáveis às de outros produtos destinados a suprir as necessidades de capital de curto prazo para as empresas, além de não revelar o custo efetivo da operação.

Sendo assim, é necessário utilizarmos as equações abaixo para transformação das de desconto em taxas de juros simples:

(1)

ou taxas de juros compostos (taxas efetivas):

(2)

A equação (1) é aplicada para transformarmos as taxas de desconto simples comercial (d) em juros simples (i), a partir da de desconto (d) e do prazo da operação (n). Já a equação (2), transforma a de desconto (d) em uma taxa efetiva de juros (i), que é o tipo empregado na maioria das operações de crédito existentes no mercado.

Página 30

Módulo 3 - Desconto Composto

1 - Desconto Composto

O desconto composto, como o próprio nome indica, baseia-se no regime de capitalização composta e é aplicado principalmente em operações de longo prazo,em cuja utilização do simples resultaria em valores absurdos.

Assim como ocorre no desconto simples, o composto pode ser classificado em dois tipos: 1) desconto composto racional ou “por dentro” e 2) desconto composto “por fora”.

Página 31

Módulo 3 - Desconto Composto

Desconto Composto Racional

Este tipo de desconto é utilizado em operações de longo prazo, as quais não se pode utilizar o simples comercial, sob pena de gerar operações com resultados absurdos, conforme demonstrado no exemplo a seguir:

Exemplo

Seja uma taxa de desconto comercial de 3% ao mês, qual o valor do desconto e o valor descontado de um título de valor nominal de R$ 10.000,00, com vencimento daqui a 3 anos?

Conforme aprendemos no módulo anterior, sendo N = 10.000; d = 0,03 a.m. e n=36 meses, então:

a) cálculo do desconto	b) cálculo do valor descontado
Dc = N x d x n	Vc = N – Dc
Dc = 10.000 x 0,03 x 36	Vc = 10.000 – 10.800
Dc = R$ 10.800,00	Vc = – R$ 800,00

O resultado acima implica dizer que, além de entregar o título ao banco, seu detentor teria de pagar R$ 800,00 pela operação de desconto, tendo em vista o valor do desconto (Dc) ser superior ao valor nominal da duplicata (N), o que, evidentemente, é uma situação absurda.

Página 32

Módulo 3 - Desconto Composto

2 - Desconto Composto Racional ou “por dentro”

Empregado em operações lastreadas por títulos de longo prazo, consiste na aplicação direta das relações próprias ao regime de juros compostos, ou seja, substituindo PV por Vrc e FV por N na fórmula de valor presente de juros compostos teremos:

(1)

Onde:

Vrc = valor descontado no desconto composto racional ou “por dentro”
N = valor nominal dos títulos objeto do desconto
i = taxa da operação
n = prazo de antecipação

Página 33

Módulo 3 - Desconto Composto

Lembrando que, na equação genérica, o valor do desconto (D) pode ser definido pela diferença entre o valor nominal (N) e o valor descontado (V), onde: D = N – V, sendo ele, no desconto composto racional igual a (Dcr) e o valor descontado igual a “Vcr”, teremos:

Drc=N-Vrc

(2)

Substituindo-se a equação (1) na (2) e resolvendo-a, têm-se:


	(3)

A equação (3) é empregada para o cálculo do valor do desconto, em operações efetuadas segundo a metodologia do composto racional.

Exercícios Resolvidos

Página 34

Módulo 3 - Desconto Composto

1) Calcular o valor do desconto composto racional de um título com valor nominal de R$ 50.000,00, descontado 12 meses antes de seu vencimento, à taxa de 2,5% ao mês.

Variaveis	Solução
Drc = ?
N = 50.000
n = 12 m	Drc = 12.822,21
i = 0,025 a.m.

Página 35

Módulo 3 - Desconto Composto

2) Quanto uma empresa receberá se descontar um título com valor nominal de R$ 30.000,00, dois anos antes de seu vencimento, a uma taxa de 3% ao mês, sabendo-se que a operação será efetuado pelo conceito de desconto composto “por dentro”?

O valor creditado à empresa é o valor descontado (Vrc), assim:

Variaveis	Solução
Vrc = ?
N = 30.000
n = 24 m	Vrc = 14.758,01
i = 0,03 a.m.

Página 36

Módulo 3 - Desconto Composto

Importante! Em operações de longo prazo, o mercado trabalha com o desconto composto racional ou “por dentro”, utilizando-o, inclusive, em operações que envolvem títulos do governo. Dado que este tipo de desconto é a aplicação do RCC, a taxa empregada é a mesma efetiva de juros do mercado, não necessitando ser transformada para fins de comparação com outras operações.

Página 37

Módulo 3 - Desconto Composto

3 - Desconto Composto “por fora”

Praticamente inexistente no mercado, o desconto composto “por fora” fundamenta-se na incidência sucessiva da taxa de desconto sobre o valor nominal do título, deduzidos aqueles acumulados em períodos anteriores.

Dessa maneira, sendo:

Vcc = Valor descontado do desconto composto “por fora”
N = Valor nominal
d = taxa de desconto
n = prazo de antecipação
Dcc = Valor do desconto do desconto composto “por fora”

As equações para o cálculo do valor descontado e para o valor do desconto são, respectivamente:

Vcc=N(1-d)ⁿ	(4)
e
Dcc=N[1-(1-d)ⁿ]	(5)

Exercícios Resolvidos

Página 38

Módulo 3 - Desconto Composto

1) Considerando uma taxa de desconto de 2% ao mês, qual o valor do desconto de um título de R$ 1.000,00, com vencimento para daqui a cinco anos, supondo-se que a operação foi realizada sob o conceito do desconto composto “por fora”?

Variaveis	Solução
Dcc = ?	Dcc=N[1-(1-d)ⁿ]
N = 1.000	Dcc=1.000[1-(1-0,02)⁶⁰]
n = 60 m	Dcc=702,45
i = 0,02 a.m.

Página 39

Módulo 3 - Desconto Composto

4 - Utilizando o Excel

1. Abra uma pasta nova que depois poderá ser arquivada com o nome de Desconto Composto.

PLANILHA DE CÁLCULO PARA DESCONTO COMPOSTO “POR DENTRO”

2. No intervalo B2 escreva: Desconto composto "por dentro".

3. No intervalo B3:D3, digite os títulos “Variáveis”, “Dados” e “Resultado”.

4. No intervalo B4:B8, indique as variáveis “Valor Nominal”, “Desconto”, “Taxa”; “Prazo” e “Valor Descontado”.

5. Usando os recursos de formatação do Excel, formate os intervalos C4:D5 e C8:D8 como moeda e o intervalo C6:D6 como percentual %, todos com duas casas decimais.

6. No intervalo D4:D8, registre as fórmulas de cálculo das variáveis “Valor Nominal”, “Desconto”, “Taxa”, “Prazo” e “Valor Descontado”, utilizando a função lógica SE, ou então digite:

6.1 Na célula D4: =SE(C4="?";C5/(1-(1/(1+C6)^C7));"")
6.2 Na célula D5: =SE(C5="?";C4*(1-(1/(1+C6)^C7));"")
6.3 Na célula D6: =SE(C6="?";-(C4/(C5-C4))^(1/C7)-1;"")
6.4 Na célula D7: =SE(C7="?";(LN(C4)-LN(C4-C5))/LN(1+C6);"")
6.5 Na célula D8: =SE(C4="?";D4-C5;SE(C5="?";C4-D5;C4-C5))

7. As fórmulas acima estabelecem as relações lógicas da função. Analisando, por exemplo, a equação da célula D4, teremos:

SE for cumprida a condição lógica C4 = “?”

ENTÃO calcule C5/(1-(1/(1+C6)^C7)) e apresente o resultado na célula D4

SENÃO registre um rótulo vazio “” na célula D4

8. Caso deseje utilizar a função SE diretamente, coloque o cursor na célula D4 e selecione INSERIR, FUNÇÃO.

9. No campo CATEGORIA escolha: LÓGICA e no campo NOME escolha SE.

10. Tomando como base a equação 6.1, no campo Teste lógico insira C4=”?”; no campo Valor_se_verdadeiro, digite: C5/(1-(1/(1+C6)^C7)) e no campo Valor_se_falso digite “”.

11. Ao final da digitação clique OK.

12. Repita os procedimentos de 8 a 11 para intervalo D5:D8, com base nas equações 6.2 a 6.5.

Página 40

Módulo 3 - Desconto Composto

PLANILHA DE CÁLCULO PARA DESCONTO COMPOSTO “POR FORA”

13. No intervalo B10 escreva: Desconto Composto "por fora".

14. No intervalo B11:D11, digite os títulos “Variáveis”, “Dados” e “Resultado”.

15. No intervalo B12:B16, indique as variáveis “Valor Nominal”, “Desconto”, “Taxa”; “Prazo” e “Valor Descontado”.

16. Usando os recursos de formatação do Excel, formate os intervalos C12:D13 e C16:D16 como moeda e o intervalo C14:D14 como percentual %, todos com duas casas decimais.

17. No intervalo D12:D16, registre as fórmulas de cálculo das variáveis “Valor Nominal”, “Desconto”, “Taxa”, “Prazo” e “Valor Descontado”, utilizando a função lógica SE, ou então digite:

17.1 Na célula D12: =SE(C12="?";C13/(1-(1-C14)^C15);"")
17.2 Na célula D13: =SE(C13="?";C12*(1-(1-C14)^C15);"")
17.3 Na célula D14: =SE(C14="?";-((1-C13/C12)^(1/C15)-1);"")
17.4 Na célula D15: =SE(C15="?";LN(1-C13/C12)/LN(1-C14);"")
17.5 Na célula D16: =SE(C12="?";D12-C13;SE(C13="?";C12-D13;C12-C13))

Lembre-se de que, independente do tipo de desconto, a unidade de tempo da taxa deve ser a mesma da operação. Caso necessite convertê-la para outro prazo, utilize o conceito daquelas equivalentes, por se tratar de “desconto composto”.

As figuras abaixo representam as planilhas construídas mediante os procedimentos descritos anteriormente:

Página 41

Módulo 3 - Desconto Composto

Resumo

Finalizando o estudo das chamadas “operações de desconto”, abordamos neste módulo as modalidades efetuadas sob a ótica do desconto composto que, assim como ocorre no simples, podem ser classificados em desconto composto “por fora” e desconto composto “por dentro”.

Ao contrário do desconto simples, no qual as operações existentes no mercado são efetuadas sob o conceito do desconto “por fora”, no desconto composto, as operações baseiam-se na metodologia de desconto “por dentro”.

Por ser construído com base na aplicação direta das relações próprias ao regime de juros compostos, a taxa de juros das operações de desconto composto “por dentro” representam as taxas efetivas negociadas no mercado, não necessitando, portanto, de conversão, a fim de que sejam passíveis de comparação com outros tipos de operações.

Página 42

Módulo 3 - Desconto Composto

As equação de calculo do valor descontado e do valor do desconto, tanto para o desconto composto “por fora”, quanto para o desconto composto “por dentro”, são apresentadas a seguir:

	(1)
	(3)
Vcc=N(1-d)ⁿ	(4)
	(5)

As equações (1) e (3), respectivamente, aplicam-se ao cálculo do valor descontado (Vrc) e do valor do desconto (Drc), em operações de desconto composto “por dentro”.

As equações (4) e (5) são utilizadas, respectivamente, para o cálculo do valor descontado (Vcc) e do valor do desconto (Dcc), em operações de desconto composto “por fora”.

Como ocorre no desconto simples, podem ser classificados em desconto composto “por dentro” e desconto composto “por fora”.