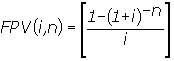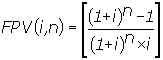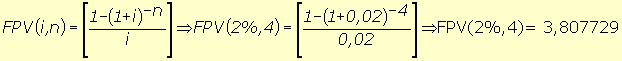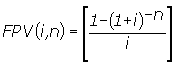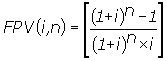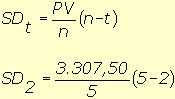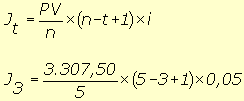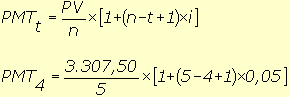PV
= PMTxFPV(i,n) e |
||
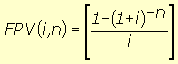
|
ou
|
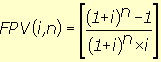 |
No exemplo:
| Variáveis | Solução |
PV
= 10.000 |
1) Calcula-se FPV (i,n) |
| i
= 0,015 a.m. |
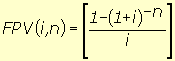 |
| n
= 6 parcelas |
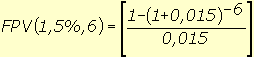 FPV(1,5%,6) = 5,697187 2) Calcula-se o valor da prestação
(PMT) 10.000 = PMTx5,697189 |
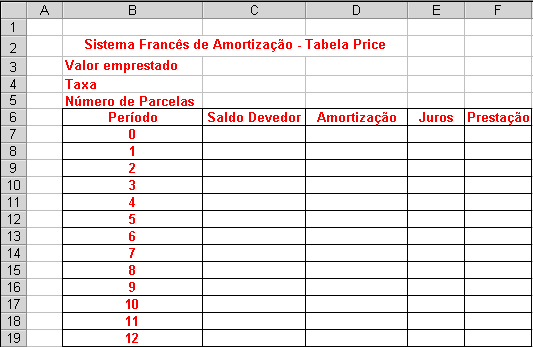
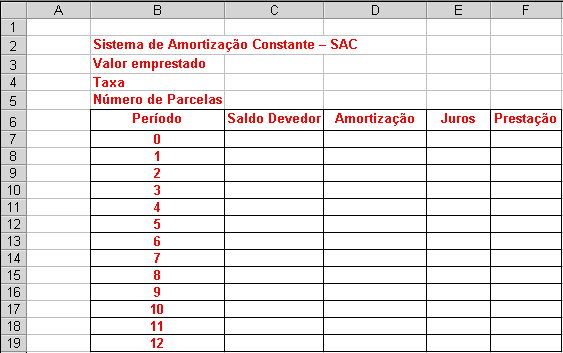
Preenchendo a tabela com o valor das prestações:
Mês |
Saldo
Devedor |
Amortização |
Juros |
Prestação |
0 |
10.000,00 |
- |
- |
- |
1 |
1.755,25 |
|||
2 |
1.755,25 |
|||
3 |
1.755,25 |
|||
4 |
1.755,25 |
|||
5 |
1.755,25 |
|||
| 6 |
1.755,25 |