Exemplo da aplicação dos dois métodos

Certa empresa poderia adquirir, por $ 300.000,00, uma nova máquina, e esta economizaria $ 29.000,00 por ano em despesas operacionais desembolsáveis. Sua vida útil estimada é de 20 anos, e o valor residual estimado é nulo.

Solução pelo Método da Taxa de Retorno Ajustada pelo Tempo.

Na verdade, segundo esta metodologia, $ 300.000,00 correspondem ao valor atual de uma anuidade de $ 29.000,00 a x % (porcentagem que estamos, justamente, procurando), durante 20 anos.

Ou, em outras palavras, que Fator (TR) poderá satisfazer na tabela de valores atuais de anuidades a equação a seguir:

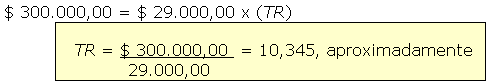
Verificando em uma tabela de Valor Atual de Anuidades e procurando, na linha de 20 anos, deve-se identificar a coluna que mais se aproxima de 10,345.

Assim, encontram-se a coluna de 6%, apontando 11,470, e a de 8%, apontando 9,818.

A verdadeira taxa ajustada pelo tempo estará entre estas duas (6 e 8%).

Assim, por interpolação, uma diferença de 9,818 (8%) menos 11,470 (6%), isto é, de 1,652, corresponde a uma diferença percentual de 2%.

A verdadeira taxa será de 8% (já que 10,345 se aproxima mais de 9,818 do que de 11,470) menos alguma coisa.

A diferença entre 9,818 e 10,345 é de - 0,527.

Assim:

Logo, a taxa verdadeira será igual a 8% menos 0,64% = 7,36%.