Delimitadores ( ),[ ],{ } - Considere a expressão 2´3+15¸5, qual o valor de tal expressão?
Alguns diriam, 9, outros, 21¸5. Cada um desses valores depende da ordem em que realizamos as operações, lembrando que as operações são realizadas entre dois números de cada vez.
Para garantir uma uniformidade de interpretação, existe uma ordem a ser seguida quando operamos com números, quais sejam:
-Primeiramente
realizamos a multiplicação e a divisão, e depois
a adição e subtração.
-Quando desejamos que esta ordem não seja seguida, introduzimos
os delimitadores ( ) (parênteses), [ ] (colchetes),
{ } (chaves), onde a ordem é seguida como foi apresentado,
primeiro realizamos as operações entre parênteses
para depois realizar as operações entre colchetes e por
final as operações entre chaves.
| Exemplo: Calcule | |
| a)
2´3+15¸5
Resolução: 6+3=9 b) (-20+45):(-5) Resolução: (25):( -5)= -5 c) (-1-4).( -10+16) - [(-8):(+2) -7 -( -1).(+5)] Resolução: (-5).(+6) -[(-4) -7-(-5)] (-5).(+6) -[-4 -7+5] (-5).(+6) -[-11+5] (-5).(+6) -[-6] -30+6= -24 |
|
Resolvendo equações do 1o Grau - Uma equação do 1o grau é uma equação da forma ax+b=c, onde a, b e c são números reais quaisquer.
| Exemplos: | |
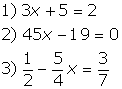 |
|
Quando dizemos 'Resolva a equação do 1o grau' queremos encontrar um valor para x que satisfaça a equação como vimos na seção sobre regras básicas. Este processo será muito útil quando nos depararmos com problemas que envolvam receita, custo, lucro, oferta e demanda do primeiro grau, que será visto no próximo módulo.
Logo, para resolver uma equação do primeiro grau precisamos apenas utilizar as regras básicas. Resolveremos alguns exercícios nesta seção para ilustrar como proceder com equações do primeiro grau.