Resolvendo Equações do 2o grau - Uma equação do segundo grau é uma equação da forma ax2+bx+c=0, onde a, b e c são números reais com a0.

Exemplo:
 

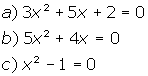Existe um algoritmo para resolver uma equação do segundo grau (encontrar os valores para x que satisfazem a igualdade), tal algoritmo recebe o nome de Fórmula de Báskhara e diz que uma equação do segundo grau pode possuir no máximo duas soluções reais determinadas pelas fórmulas:

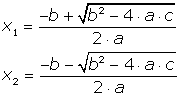
A expressão dentro do radical recebe o nome de discriminante e é representado pela letra grega maiúscula  (delta), assim:
x1 e x2 recebem o nome de raízes da equação do segundo grau.

Exemplo:
Encontre as soluções das equações do segundo grau (encontre as raízes) a seguir:
  a) x2-3x+2=0
Resolução:
  Temos que a=1 b=-3 e c=2 e pelas fórmulas de Baskhara, obtemos:
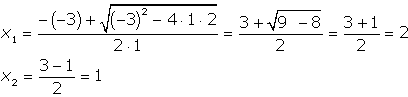Logo o conjunto solução da equação é {-1,2}. Observe que D=1 >0

b) x2-2x+1=0
Resolução:
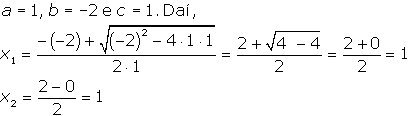Neste exemplo, as duas raízes são iguais. Observe que D=0

c) 3x2+3x+1=0
Resolução:
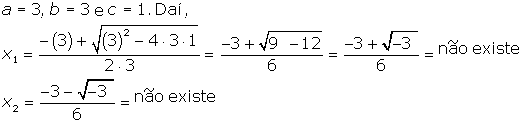Neste exemplo, as duas raízes não existem. Observe que D<0.

Em geral uma equação do segundo grau ax2+bx+c=0 pode ser escrita como um produto de fatores de 1o grau, se a equação possuir raízes reais, da seguinte forma:

Exemplo:
  a) A equação x2-3x+2= (x-1)(x-2) =0
b) A equação x2-2x+1= (x-1)(x-2) = (x-1)2 =0
c) Não é possível fatorar 3x2+3x+1 pois a mesma não possui raízes reais.

Desafio:
A raiz quadrada da metade do número de abelhas de um enxame passou voando por cima de um jasmineiro; oito nonos do total do enxame tinham ficado na colméia, mas uma abelha fêmea que saiu ficou voando em torno de um macho que está zumbindo no interior da flor de lótus para onde foi atraído por seu suave perfume, lá ficando aprisionado. Quantas são no total as abelhas?

Resposta


Copyright © 2019 UPIS.