Dada a função f(x) = 2x-1 então será:

a) 1 b) 4 c)2/7 d) 3 e) 2

Resposta:

Dada encontre .

a) 3 b) 8/3 c) 2 d) 4 e) 0

Resposta:

O custo mensal fixo de uma fábrica que produz esquis é R$4.200, e o custo variável é de R$55,00 por par de esquis. O preço de venda é R$105,00 por par de esquis. Se x pares de esquis são vendidos durante o mês expresse o lucro mensal como função de x.

a) 40x-1500 b) 50x-4200 c) 3200 d) 3x-3900 e) 40x-4000

Resposta:

Gráficos - Existe um provérbio Chinês que diz que uma figura vale mais do que mil palavras. Isto se aplica muito em matemática. No caso de funções a representação de seu gráfico, é a figura que vale mais do que mil palavras.

Definição: O gráfico de uma função f é o conjunto dos pares (x, f(x) ) (clínica plano cartesiano), onde x percorre o domínio de f.
Quando a função é dada por uma equação y = f(x), seu gráfico nada mais é que o conjunto-solução dessa equação. Com a representação do gráfico, a gente "vê" o comportamento da função, o que, na maioria das vezes, é difícil só com a expressão. Vamos esclarecer este ponto com um exemplo prático:
Um fazendeiro quer construir uma benfeitoria em sua fazenda, chega à conclusão de que o custo da obra, em dólares, é dado por:

onde x é a medida em metros de um lado da construção.
Vejamos alguns valores para esta relação:

• Se o lado medir x = 1 metro, o custo será:

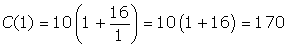
  dólares.

  
  
• Se o lado medir x = 2 metros, o custo será:

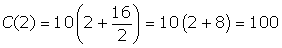
  dólares.

Podemos fazer as seguintes perguntas:
- Quando x aumenta, o custo aumenta ou diminui?
- Qual o valor de x que dá o menor custo?

Olhando só para a expressão de C(x), fica difícil responder tais perguntas. Vamos agora exibir uma representação do gráfico da função C(x).

Se soubermos interpretar tal representação corretamente, vamos poder começar a responder as perguntas anteriormente formuladas. De fato, quando x aumenta, a curva vai abaixando, até que x atinja 4 ( isto significa que o custo está diminuindo); daí em diante, a curva vai subindo (o que significa que o custo está aumentando). Pela representação do gráfico vemos que o custo mínimo ocorre para x =4, e este custo mínimo é .
Com este exemplo prático podemos concluir que através da representação gráfica da função em estudo, podemos obter informações importantes que poderão nos auxiliar na elaboração de projetos.
Posteriormente iniciaremos o estudo das principais funções elementares e nestas unidades mostraremos como construir seus gráficos.