Vamos considerar agora a função f(x)=x³+5x²+3x+7.Calculando os valores para. Obtemos a seguinte aproximação do gráfico de f(x).

Começamos, construindo a tabela:

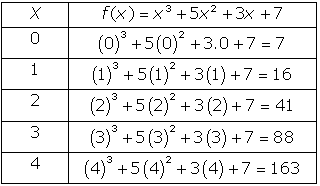
Em seguida, marcamos os pontos no plano cartesiano:

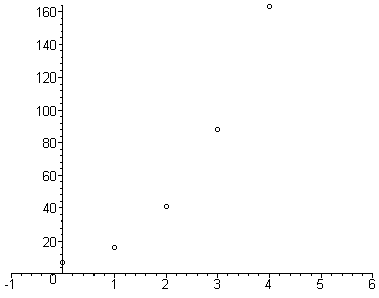
Em seguida unimos os pontos por uma linha suave.

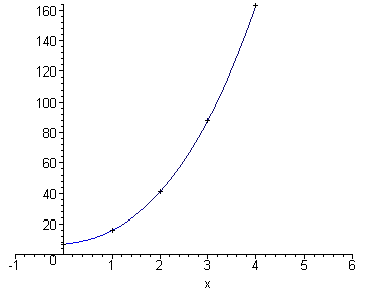
Entendido!!

Talvez este gráfico fosse bem representativo de um problema em que a variável x não pudesse ser negativa. Mas e se a variável x pudesse ser negativa? Não teríamos idéia do comportamento da função. Na verdade o gráfico da função acima toma valores bem interessantes para valores negativos de x, vejamos.
Vamos considerar agora que x Î {-3,-2,-1,0,1,2,3,4} ou seja acrescentamos três valores negativos ao conjunto tomado anteriormente.
Marcando os pontos obtidos no plano cartesiano e unindo por uma linha suave. teríamos:

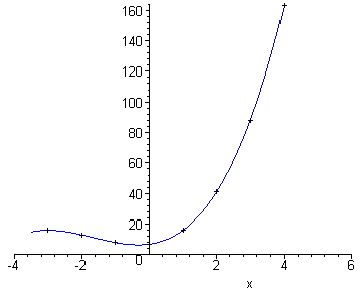
Observe então que a escolha dos pontos que marcaremos no plano cartesiano é fundamental na hora da construção do esboço do gráfico de uma função.

Quando possuímos a regra de uma função e queremos saber se um ponto pertence ao gráfico da função substituímos as coordenadas do ponto da regra da função e verificamos se obtemos uma identidade. Confuso?! Vejamos em exemplos.