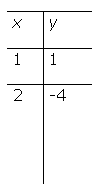2 - Principais Funções Elementares
Função Constante é toda função do tipo y = k (onde k é uma constante real). O gráfico de tal função é uma reta horizontal, passando pelo ponto de ordenada k.
Assim, o domínio são os reais.
Exemplo: y = f(x) = 2.
Lembrando que o gráfico de uma função é o conjunto dos pontos (x,f(x)). Vamos encontrar alguns valores do conjunto (x, f(x)).
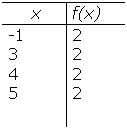
Observe que para qualquer valor de x obtemos sempre o mesmo valor para y.
Função do 1º grau (ou função linear) é toda função com a seguinte definição: y = mx + n, onde m e n são constantes e m¹0.
Prova-se que o gráfico de tal função é uma reta. Dessa forma ele pode ser obtido através de dois pontos. (Isto é possível devido ao seguinte resultado da geometria plana: Por dois pontos distintos determinamos uma única reta).
Exemplos:
a) Vamos esboçar o gráfico da função y
= 2x+1.
Observe que a função acima é linear (compare com
(*)). Assim sabemos que seu gráfico é uma reta, logo basta
encontrarmos dois pontos que satisfaçam a equação
acima para identificarmos o gráfico de y = 2x+1.
A seguir veremos como encontrar tais valores.
Atribuindo a x os valores 0 e 1 (lembre-se que os valores de
x são independentes, logo podem assumir qualquer valor
no domínio da função) teremos:
|
x
= 0 Þ y = 2.0+1 = 0+1
= 1, |
Encontramos para x=0 o valor de y=1 e para x=1 o valor de y=3. Assim podemos formar os pares ordenados (0,1) e (1,3).
Logo a reta procurada passa pelos pontos (0,1) e (1,3) e seu gráfico é o da figura abaixo:
Esboce
o gráfico das funções:
a)
y=5
b) y=-5x+6
Resoluções:
b)