Funções elementares

Algumas funções são muito utilizadas e por isso dedicaremos um tempo maior a elas. Muito do que utilizaremos neste módulo já foi visto e tratado nas unidades anteriores (expressões algébricas, equação polinomial, equação do segundo grau), qualquer dificuldade que tiver procure retornar a tal unidade para rever os conceitos tratados por lá.

Função do 1º Grau (Função Linear).
Como o próprio nome já diz trata-se de uma função cujo gráfico imita uma linha reta. A representação geral de uma função linear é:

Ou, se preferir,

O coeficiente m é dito coeficiente angular da reta ou inclinação da reta e o coeficiente n é dito coeficiente linear da reta. A inclinação está diretamente ligada ao angulo que a reta forma com o eixo das abscissas.
Não entraremos em detalhes aqui, mas a inclinação de uma reta é justamente a tangente do angulo formado pelo eixo x e a reta medida no sentido ante horário a partir do eixo x. Precisaríamos, para entender melhor o assunto, de um certo conhecimento de trigonometria e isto ainda não foi visto.

Exemplo:
São exemplos de funções lineares:

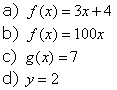
Vejamos o gráfico de uma função linear. Tomemos, por exemplo, .
Escolhendo , conseguiremos o seguinte esboço do gráfico.

Na verdade, para esboçar o gráfico de uma função linear, precisamos apenas marcar dois pontos.
Você já ouviu dizer que dois pontos distintos determinam uma única reta? E isso é pura verdade.
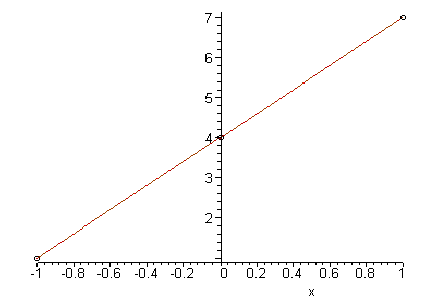
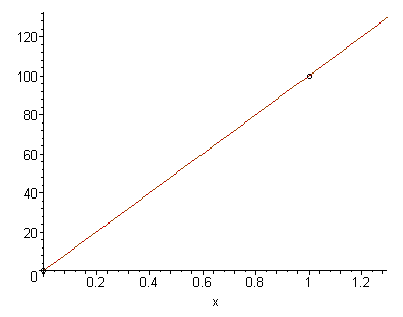
Façamos mais um. Considere, agora, a função , escolhendo teremos:

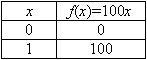
E se a função fosse da forma f(x)=n, com n ?

Quando a função tem esta forma, dizemos que a função é constante pois, para qualquer valor de x,obtemos sempre o mesmo valor para f.

Exemplo:
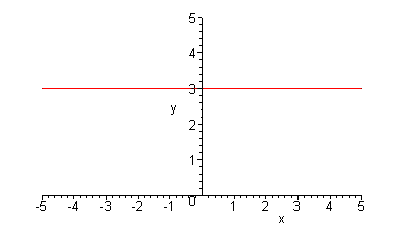
Esboce o gráfico da função função f(x)=3. Neste caso, se fossemos construir a tabela de valores, obteríamos sempre a mesma imagem, 3, para qualquer que seja o valor de x. O gráfico então seria uma reta paralela ao eixo x, passando pelo 3, como segue:

Construir o gráfico de uma função linear quando é dada sua regra é até fácil, basta marcar dois pontos no plano cartesiano. Mas e se quiséssemos obter a função que representa a reta que passa por dois pontos dados, como devemos proceder? É o que veremos a seguir.
Obtendo a função linear a partir do gráfico.