Queremos obter a equação da reta que passa pelos pontos (2,4) e (3,5). Na figura a seguir colocamos os dois pontos no plano cartesiano.

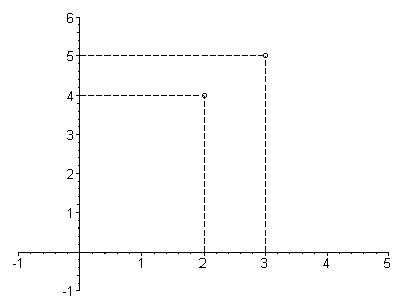
Agora, uma reta tem a forma f(x)=mx+n , onde x pertence ao domínio da função e f é a imagem de x.
Como os pontos (2,4) e (3,5) têm que satisfazer a equação da reta, devemos ter que:

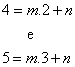
Se encontrarmos os valores de m e n teremos conseqüentemente obtido a função para toda a reta que passa pelos pontos dados.
Resolvendo o sistema obtemos m=1e n=2.
Ou seja, f(x)=x+2. Se quisermos saber se um ponto pertence ou não à reta, basta substituir as coordenadas do ponto na função da reta e verificar se verifica ou não a igualdade, vejamos.

Exemplo:
Verifique se o ponto (1,2) pertence a reta f(x)= x+2.
Resolução

Substituindo o ponto, obtemos
2=1+2 o que não é verdade, pois 2 não é igual a 3.

Exemplo:
Verifique se o ponto (5,7) pertence a reta f(x)= x+2.
Resolução:

Substituindo o ponto, obtemos 7=5+2, o que é verdade.
Logo o ponto (5,7) pertence à reta dada.

Exemplo:
Determine a função da reta que passa pelos pontos (2,4) e (7, -1).
Resolução:
Precisamos encontrar então os valore de m e n. Substituindo os pontos na equação.

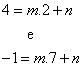
Isolando n na primeira equação, obtemos, n=4-2m. Substituindo n na segunda equação, obtemos  daí,   , isolando m obtemos . Encontramos um dos valores, falta o segundo, vamos lá. Já sabemos , substituindo , n = 4-2(-1) = 4 + 2 = 6. Encontramos os dois valores, logo a função da reta que passa pelos pontos dados será:

f(x) = - x + 6