Para esboçar
o gráfico de uma função do segundo grau nos concentraremos
em determinar apenas quatro pontos no máximo: o vértice,
as raízes (no máximo duas), e o intercepto y.
Para encontrar as raízes procedemos como no caso de polinômio
do segundo grau, utilizamos a fórmula de Báskhara. Logo
![]()
Onde
a,b e c são os coeficientes do polinômio.
Para encontrar as coordenadas do vértice da parábola, utilizamos
as seguintes equações
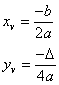
O intercepto y, é o ponto onde x=0, para determinar tal ponto basta, portanto, substituir x por zero na função e encontraremos o termos independente c. Logo o intercepto y é o ponto (0,c).
Exemplo:
Esboce o gráfico da função ![]() .
.
Resolução:
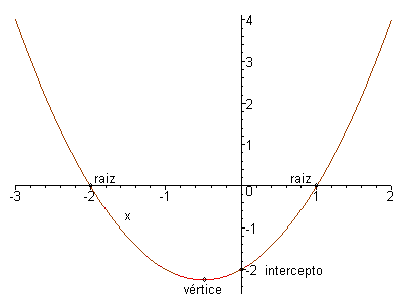
Utilizaremos então apenas os quatro pontos mencionados acima.
Comecemos pelas raízes da equação. Temos que a=1,
b=1e c = -2.
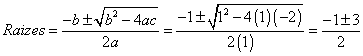
Logo x= -2 e x=1 são as raízes do gráfico da função.
Passemos ao vértice da parábola.

Lembre-se
de que ![]()
Falta
agora o intercepto y, que é o ponto .
Marcando estes pontos no plano cartesiano, obtemos o seguinte gráfico.