Comumente, deparamos com divisões e, em se tratando de funções, podemos nos deparar com variáveis no denominador da divisão. Trataremos aqui um caso particular de função em que ocorrem variáveis no denominador, as funções racionais, cuja definição será dada a seguir. Uma aplicação de tal função será dada ao final da seção após um entendimento melhor de seu comportamento.

Uma função racional é uma função da forma :

Claramente, o domínio de f(x) não poderá incluir as raízes do polinômio do denominador. (Raiz é ponto onde o polinômio se iguala a zero, e não existe divisão por zero).

Exemplo:

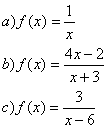
Trataremos apenas de funções racionais formadas por polinômios de grau menor ou igual a 1.
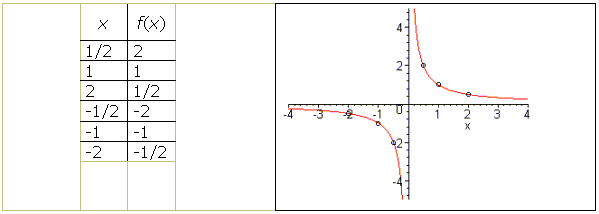
Façamos o gráfico de , por marcação de pontos.

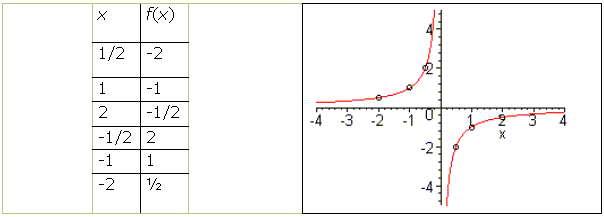
Agora vejamos o gráfico de.

Os gráficos de funções racionais cujos graus do denominador seja igual a um e o grau do numerador seja zero ou um terá um aspecto parecido com um dos gráficos acima. Veremos em exemplos a seguir: