|
Observação:
Se a igualdade se verifica para todo x de D, tem-se uma identidade (em
D). Caso contrário, tem-se uma equação. Neste
último caso, resolver uma equação significa achar
os x de D que a verificam, o conjunto deles sendo chamado de conjunto-solução
da equação (tal conjunto pode não conter nenhum elemento,
que é o caso de não haver solução da equação).
Exemplo:
1-Para a igualdade 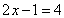 ,tem-se D=
,tem-se D=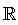 .
Tirando o valor de x, chega-se a .
Tirando o valor de x, chega-se a 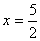 , logo se trata de uma equação, cujo conjunto-solução
é
, logo se trata de uma equação, cujo conjunto-solução
é 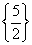 . .
Não
entendeu como encontramos o valor de x?
2- Para a
igualdade 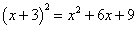 , tem-se D=
, tem-se D=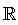 . .
Como 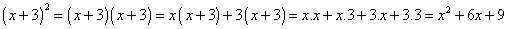
Então
a igualdade é uma identidade.
3- Para a igualdade 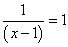 , tem-se que D=
, tem-se que D=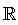 -{1}.
Ela equivale a 1=x-1, logo a x=2. Portanto, trata-se de
uma equação, cujo conjunto-solução é
{2} -{1}.
Ela equivale a 1=x-1, logo a x=2. Portanto, trata-se de
uma equação, cujo conjunto-solução é
{2}
4-Para a
igualdade
tem-se D=¡-{1},
logo trata-se de uma identidade, pois vale para todo x de D.
Nomenclatura
Evitaremos entrar na definição formal de polinômio,
pois foge ao intuito desta clínica. Podemos dizer, sem compromisso,
que uma expressão polinomial é soma de parcelas do tipo
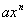 , a real e n natural (se n=0 convenciona-se que
, a real e n natural (se n=0 convenciona-se que 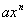 é a).a). No caso de duas letras, x e y é a
mesma coisa, o tipo sendo
é a).a). No caso de duas letras, x e y é a
mesma coisa, o tipo sendo 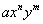 , m natural.
, m natural.
Os números
que multiplicam as potências nas expressões e os que figuram
localmente são chamados de coeficientes. Assim, 7, -6 e 2 são
coeficientes de 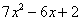 , e 4, -8 e 1 são coeficientes de
, e 4, -8 e 1 são coeficientes de 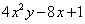 . .
Cada parcela
da expressão polinomial é referida como termo. Assim, 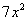 , 6x e 2 são termos de
, 6x e 2 são termos de 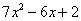 . O termo no qual não aparece x é chamado de termo constante.
. O termo no qual não aparece x é chamado de termo constante.
Os termos 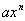 e
e 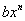 são chamados termos semelhantes, como por exemplo
são chamados termos semelhantes, como por exemplo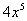 e
e 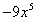 . No caso de duas letras x e y: os termos
. No caso de duas letras x e y: os termos 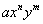 e
e 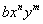 são
chamados termos semelhantes (por exemplo são
chamados termos semelhantes (por exemplo 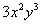 e
e 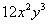 ). A definição para o caso de mais letras é obvia.
). A definição para o caso de mais letras é obvia.
A expressão polinomial nula é formada apenas pelo
termo constante nulo, e é indicada por 0.
|