Identidades Envolvendo divisão
Antes de
falar de divisão de polinômios, falemos sobre divisão
de inteiros.
Dados os inteiros positivos a e b, existe um único par ordenado
(q,r) de números inteiros tal que a= bq+r, com 
q e r são chamados quociente e resto, respectivamente, da divisão euclidiana de a e b. Neste contexto, a e b são chamados dividendo e divisor, respectivamente.
Exemplo:
Se dividirmos 23 por 4 obteremos quociente 5, e resto 3, pois 23=4.5+3. Da igualdade anterior resulta
Em geral,
Para efetuar a divisão praticamente, existe um algoritmo, chamado algoritmo da divisão, que ilustramos com o exemplo a seguir, no qual dividimos 1546 por 54:
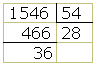
Ou seja, 1546 = 54.28+34
Existe um teorema análogo que diz respeito à divisão de uma expressão polinomial por outra. Para enunciá-lo, introduziremos a seguinte nomenclatura:
Se na expressão
polinomial 
tem-se 
ela é dita ter grau n; n é chamado de grau
da expressão.
Em outras palavras, o maior expoente de um polinômio determina o seu grau.
Exemplo:
tem grau 3, 
tem grau 4. Uma expressão polinomial constante, isto é,
formada apenas pelo termo constante, tem grau 0.
Temos então, o seguinte resultado:
Se A
e B são expressões polinomiais, 
,
então existe um único par (Q,R) de expressões
polinomiais tal que tem-se a identidade A=BQ+R, com R=0
ou grau de R< grau de B.
Q e R são chamados quociente e resto, respectivamente, da divisão euclidiana de A por B. Neste contexto, A e B são chamados dividendo e divisor, respectivamente.
Existe um algoritmo para efetuar a divisão de duas expressões polinomiais, análogo ao da divisão de números.
Exemplo:
Dividir 
por 
. Primeiramente escrevemos o dividendo como soma das parcelas de potências
decrescentes de x, colocando 0 quando a potência não
comparece. Fazemos o mesmo com o divisor, se necessário. Daí:
Dividimos
( primeira parcela do dividendo) por 
( primeira parcela do divisor) e obtemos 5x (primeira parcela do
quociente):
Multiplicamos
5x pelo divisor, mudando o sinal, para obter
, escrevemos isto abaixo do dividendo para somar com ele:
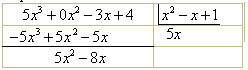
Abaixamos
o próximo termo do dividendo, a saber 4, obtendo 
.
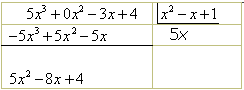
Repetimos
o processo, com
omo dividendo. Então dividimos 
por 
para obter 5, que vai ser a segunda parcela do quociente. Multiplicamos
5 pelo divisor, mudamos o sinal, para obter 
,
que deverá ser escrito abaixo do novo dividendo, para somar com
ele:
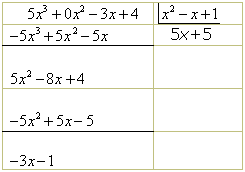
Como
a expressão obtida -3x-1 tem grau 1, menor que o
grau 2 do divisor ,
devemos parar por aqui.
Portanto o quociente é 5x+5 e o resto é -3x-1.
Observação:
O processo de divisão acima nos permite escrever então a
identidade em 
ou então
Exemplo:
Divida 
por 
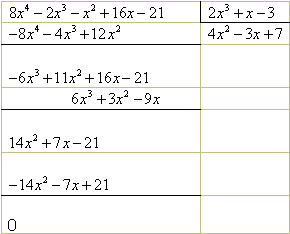
Portanto,
o quociente é 
e o resto é 
.
Observação:
De
acordo com o resultado acima, podemos escrever a identidade em
ou,
para todo x real tal que 
