Dispositivo de Briot-Ruffini

Apresentaremos um dispositivo que facilita a divisão de polinômios quando o divisor é da forma x- a. Vejamos no exemplo a seguir:

Exemplo:

Divida

Resolução:

Dispomos o dividendo em soma de parcelas de potências decrescentes de x, e dispomos as expressões como na divisão de números, só que agora escreveremos os coeficientes (os números que multiplicam as potências de x). No caso, o dividendo se escreve , os coeficientes sendo 2, 0, -3, 1 e -3, dispomos os números como segue:

A seguir, baixamos o primeiro coeficiente, 2, isto é, escreveremos 2 abaixo do 2. Daí multiplicamos esse número pelo número na chave da divisão, isto é, por 3, resultando em 2.3=6. O número obtido é somado ao segundo coeficiente do dividendo, sou seja, 6+0=6, e o resultado é escrito abaixo desse segundo coeficiente.

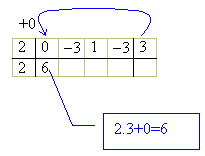
Agora, repetimos o procedimento, começando pelo 6. Multiplicamos 6 pelo número da chave 3, e somamos com -3, obtendo 15, o qual colocamos abaixo do próximo coeficiente do dividendo, isto é, abaixo do -3:

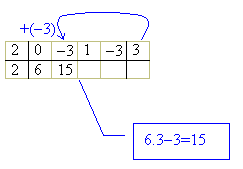
De novo: multiplicamos 15 por 3 e somamos com o coeficiente seguinte 1, para obter 46, que colocamos abaixo desse coeficiente.

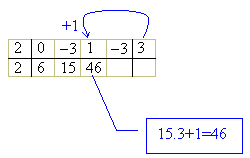
Finalmente, a última etapa: multiplicamos 46 por 3 e somamos com -3, obtendo 135, que deve ser colocado abaixo de -3. O número 135 é o resto. Veja como fica o dispositivo:

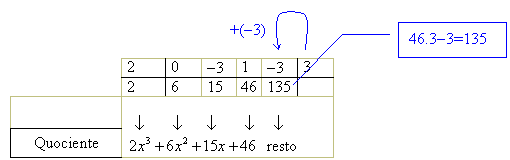
O quociente é obtido através dos números da segunda linha, exceto o último, 135, que é o resto. Deve-se começar com uma potência a menos que a do dividendo. Então o quociente é, conforme indicado acima, . Portanto:

ou, se

Exemplo:

Usando o dispositivo de Briot-Ruffini, efetue a divisão de por x+2, em seguida escreva como um produto. Procedendo como visto acima, resulta:

Note que x+2=x-(-2). Temos que o quociente é , e o resto é 0. Portanto, podemos escrever

Lembrando:
O dispositivo de Briot-Ruffini, só pode ser empregado quando o divisor for da forma x- a.