Fatoração

Fatorar uma expressão significa escrevê-la como um produto. Veremos alguns casos mais utilizados de fatoração. Quais sejam:

Caso 1:

Exemplo:
1- Para fatora , observemos que , e que . Além disso, fazendo aparecer o fator 2 na segunda parcela, temos 12x=2.6x=2.3x.2 e assim,

2- Para fatorar , notemos que , , e que

12.a=2.6.a=2.6.a.1, logo

Caso 2:

Exemplo:

1-Para fatorar , devemos achar m e n tais que m.n=12 e m+n=8. Tentemos achar m e n inteiros. Como 12 tem fatores 1 e 12, 2 e 6, 3 e 4, vemos que 2 e 6 somam oito, logo tomamos m=2 e n=6. Então

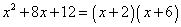
Caso 3:

Exemplo:

1-Para fatorar , escrevemos

Exemplo:
Podemos fatorar expressões com grau maior que 2 se for possível recair numa expressão de grau 2. Por exemplo,

Caso 4 :

Exemplo:
Para fatorar , escrevemos

Caso 5 :

Este caso pode ser deduzido do anterior, bastando notar que , de modo que

Exemplo
Vamos fatorar .

Observação:
Dada uma expressão polinomial, se substituirmos x por um número, obtemos um número real, chamado valor da expressão nesse número. Assim, se a expressão , o seu valor em x=1 é . E o seu valor para x=0 é 1, como se pode verificar. Um número no qual a expressão se anula é chamado de raiz da equação polinomial. Assim, 1 é raiz de , pois . Ou seja, 1 é raiz da equação . Se conhecemos uma raiz de uma expressão polinomial, há possibilidade de começar a fatorar a expressão. Na verdade se c é raiz de A, então a divisão de A por x-c é exata, isto é, tem resto 0.

Exemplo:
Como 1 é raiz de , pelo que adiantamos acima, tal expressão polinomial é divisível por x-1. Usando o algoritmo de Briot-Ruffini, temos

Portanto, onde usamos, na última igualdade, o procedimento do caso 2.