Exemplo: Para a função anterior, calcule:

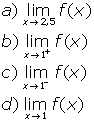
Resolução:

	a) Como 2,5 é maior que 1, para o cálculo do limite utilizaremos apenas a parte y=x2, daí:
	b) Devemos determinar o valor que f(x) se aproxima quando aproximamos por valores maiores que 1. Novamente, observamos que para valores maiores que 1 devemos utilizar a regra y=x2, daí:
	c) Devemos, agora, determinar o valor que f(x) se aproxima quando x toma valores próximos de 1 mas menores que 1. Para valores de x menores que 1 devemos utilizar a regra y=2x+4, daí:
	d) E agora como devemos proceder? Devemos utilizar a primeira, ou a segunda regra da função para calcular o limite?

Na verdade para determinar , devemos, calcular e se ambos existirem e forem iguais então o existirá e terá o mesmo valor. No nosso caso como os limites laterais são diferentes, isto é, ¹ , pelos itens b) e c),desta forma não existe.
Graficamente, visualizamos podemos perceber que pelo lado esquerdo a imagem da função se aproxima de 6 e pelo lado direito a imagem se aproxima de 1.

Observação: No item a) não calculamos os limites laterais por que a função tanto a esquerda quanto a direita de x=2,5, para valores próximos de x=2,5, é uma só, o que não ocorre para x=1 que a direita é uma regra e a esquerda é outra regra.