2 - Cálculo de Derivadas

A derivada é uma técnica matemática de excepcional poder e versatilidade. É um dos dois conceitos centrais do ramo da matemática chamado Cálculo, e tem diversas aplicações, incluindo traçado de curvas, otimização de funções (encontrar pontos de máximos e mínimos de funções) e análise de taxas de variação. Apresentaremos inicialmente um problema prático que pode ser resolvido usando o cálculo.

Problema de Otimização - Um produtor pode produzir rádios ao custo de R$2,00 a peça. Os rádios são vendidos por R$5,00 cada, e a esse preço, os consumidores têm comprado 4000 rádios por mês. O produtor está planejando elevar o preço dos rádios, e estima que para cada R$1,00 de aumento serão vendidos por mês 400 rádios a menos. Expresse o lucro mensal do produtor em função do preço de venda dos rádios. Qual seria o preço ótimo de venda?

Solução:

Vimos anteriormente que
x = preço de vendas
Lucro = (nº de rádios vendidos) (lucro por rádios)
Números de rádios vendidos = 4000 - 400 (números de aumentos de R$1,00)
Número de aumentos de R$1,00 = x - 5, ou seja é a diferença entre o preço novo de venda e o antigo.
Logo,

Números de rádios vendidos = 4000 - 400(x-5) = 400(10 - (x-5)) = 400(15-x)
Lucro por rádios vendidos = x - 2

Assim
Lucro = L(x)=400(15-x)(x-2)
A função lucro é uma função quadrática. Vimos que seu gráfico é uma parábola.

Gráfico

Queremos determinar o valor de x de tal forma que tenhamos o lucro máximo. Este é um problema típico de otimização. Nas unidades anteriores determinamos o máximo de uma função do 2º grau como sendo o ponto do vértice, quando a parábola é côncava para baixo.
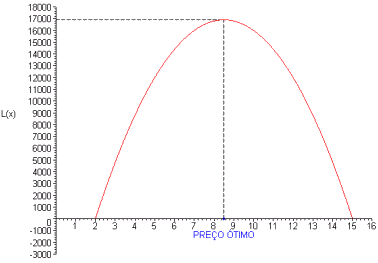
Agora daremos um procedimento diferente para determinar o ponto de máximo de qualquer função, lembremos que nem toda função é do 2º grau.