Exemplo 3:

a) Encontre a derivada da função f(x)= .

b) Encontre a equação da reta que é tangente ao gráfico da função f(x)= quando x=2.

Solução:

a) Vamos calcular a diferença

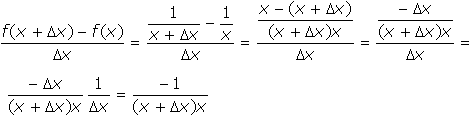
Calculando o limite quando Dx®0, teremos

f'(x)=

b) Queremos determinar a equação da reta tangente no ponto x=2. Sabemos que a inclinação será a derivada no ponto x=2, assim

Para x=2 temos que y=f(2)= . Temos assim a inclinação da reta m=-1/4 e o ponto cuja coordenada é (2,1/2), assim teremos a reta

Substituindo o ponto (2,1/2) na equação acima encontraremos o valor de n.

Portanto a equação da reta tangente no ponto x=2 é

Encontre o ponto no qual a derivada da função lucro L(x)=400(15-x)(x-2) apresentada no início da unidade, é igual a zero, ou seja L'(x)=0.