Derivadas
1) A equação da reta tangente ao gráfico de ƒ(x)= x2 + x + 1 no ponto x = 2 é:
Resolução:
1° Passo) Determinar o coeficiente angular da reta
Coeficiente angular da reta tangente é definido como sendo a derivada da função, no ponto = m = f ‘(x0)
Então vamos determinar a derivada da função e calcular o valor da derivada no ponto x =2:
ƒ
'(x)= 2x + 1
ƒ
'(x)= 2 . 2 + 1= 4 + 1= 5
Logo m=5.
2° Passo) Calcular a equação da reta
Equação
da reta é dada pela regra:
y = mx + n
Como m=5 e para x=2 encontraremos f(2)=(2)2 + 2 + 1=7, logo temos o coeficiente m = 5 e o ponto (2,7).
Portanto
a equação será:
y=5x+n, substituindo o ponto (x=2, y=7), encontraremos o valor de n:
7 = 5.2 + n logo n= -3.
Assim a equação é:
y = 5x - 3
1) 2) Derive
![]() .
.
Resolução:
Inicialmente iremos escrever a função em forma de potência
![]()
Usando as regras de derivação:
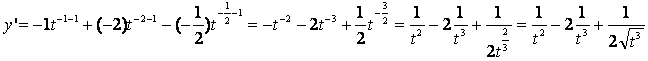
3) A receita anual bruta de uma certa companhia foi de A(t)= 0,1t2 + 10t +20 mil unidades monetárias, t anos após sua fundação em 1991.A que taxa percentual a receita anual bruta estava crescendo em relação ao tempo em 1995?
1° Passo) Definição de taxa percentual
Taxa percentual
= ![]()
Observação) Estou considerando t = 4, por que a fundação foi em 1991 e o tempo solicitado é 1995, então de 1991 para 1995 passaram 4 anos, ok?
2°) Passo
Determinar os termos da definição, ou seja, A’(4) e o A(4).
A'(t)=
0,2t + 10
A'(4)= 0,2.4 + 10 = 0,8 + 10= 10,8
A'(4)= 0,1(4)2 + 10.4 + 20= 61,6
Substituindo os valores nas expressões acima:
Taxa percentual
= ![]()
4) Suponha
que u e v sejam funções de x deriváveis em x = 0
e que
u(0)=
5 u'(0)=
3
v(0)=
-1 v'(0)=
2
Encontre
o valor da derivada ![]() em x = 0.
em x = 0.
Resolução:
1° Passo)
A regra do produto é dada por:
![]()
2° Passo) Substituindo x = 0 na expressão acima, em seguida substitua os valores dado no enunciado, isto é:
u(0)=
5 u'(0)=
3
v(0)=
-1 v'(0)=
2
![]()