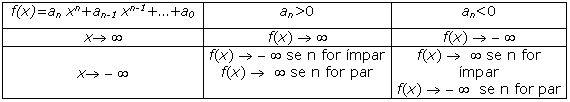Resumo
A idéia fundamental de um limite: "de qual valor f se aproxima (tende) a medida que nos aproximamos de (tendemos a) um valor não necessariamente pertencente domínio de f por valores pertencentes ao domínio de f "
,
procederemos da seguinte forma:- Se obtivermos um valor real, tal valor será o limite de f(x) quando x se aproximar de a.
- Se por acaso nos depararmos com uma divisão da formacom c¹0, então
, o que veremos com mais detalhes na próxima seção.
- Se nos depararmos com uma divisão da forma, então deveremos reescrever a função de forma a recair em um dos dois casos anteriores.
-Limites
infinitos e no infinito
Se 
,
então:
- se c>0 e g(x) tender a zero por valores positivos então
;
- se c>0 e g(x) tender a zero por valores negativos então
;
- se c<0 e g(x) tender a zero por valores positivos então
- se c<0 e g(x) tender a zero por valores negativos então
O resultado acima também é válido se tratarmos de limites laterais.
onde r é um número real positivo.