Procedimento para encontrar os pontos de máximo ou mínimo de uma função ƒ(x):
1º Passo) Encontrar os pontos críticos da função resolvendo a equação ƒ'(x) = 0.
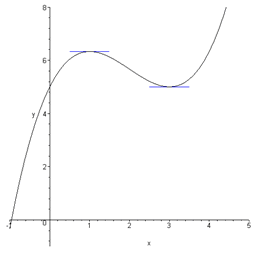
Analisando o gráfico acima pode-se observar que os pontos de abscissa x = 1 e x = 3, são, respectivamente, pontos de máximo e mínimo. Observe que a reta tangente à curva nesses pontos é uma reta horizontal, sem inclinação, ou seja, ƒ'(x) = 0. Assim, podemos intuitivamente concluir que se x0 é um ponto de máximo ou mínimo, então . Estes pontos x0 são chamados de pontos críticos e são determinados resolvendo a equação ƒ'(x) = 0. Dessa forma, se uma função tem um ponto de máximo e/ou mínimo, este também será um ponto crítico.
2º Passo) Aplicar o teste da 2ª Derivada para determinar qual ponto é de máximo e qual ponto é de mínimo.
Determinados os pontos críticos, surge, porém, um problema: Quais desses pontos críticos será de máximo, mínimo ou nem de máximo nem de mínimo? Este problema deverá ser resolvido utilizando o Teste da 2ª Derivada, que diz o que segue.
Seja x0 um ponto crítico e ƒ''(x) a segunda derivada da função ƒ(x),
Se ƒ''(x0 ) > 0 então x0 é um ponto de mínimo.
Se ƒ''(x0 ) < 0 então x0 é um ponto de máximo.